

| MATLAB Function Reference |   |
Syntax
[A,B,C,...] = gallery('tmfun',P1,P2,...)
gallery(3) a badly conditioned 3-by-3 matrix
gallery(5) an interesting eigenvalue problem
Description
[A,B,C,...] 回傳字串 = gallery('tmfun',P1,P2,...)
tmfun 指定的測試矩陣。tmfun 是矩陣家族的名稱,列於下表。P1, P2,... 是各矩陣家族所需的輸入參數。各矩陣家族的輸入參數個數詳述於後。
cauchy--Cauchy 矩陣
C = gallery('cauchy',x,y)
回傳 n x n 矩陣,C(i,j) = 1/(x(i)+y(j))。x、y 是長度為 n 的向量。若傳入的 x、y 是純量,函式自動轉換為 1:x 與 1:y 的向量。
C = gallery('cauchy',x)
回傳與上列相同的矩陣,只是 y = x。也就是回傳 C(i,j) = 1/(x(i)+x(j))。
若 x、y 內都沒有相同的元素,行列式 det(C) 非為零。若 0 < x(1) <... < x(n) 且 0 < y(1) < ... < y(n),C 為正。
chebspec--Chebyshev spectral differentiation 矩陣
C = gallery('chebspec',n, 回傳 switch)
n 階次的 Chebyshev spectral differentiation 矩陣。switch 是一個變數,決定回傳矩陣的性質。switch 的初始值為 0。
當 switch = 0 (未設定邊界狀況),C 是冪零的(nilpotent)(Cn = 0) 且具有空向量 ones(n,1)。矩陣 C 與特徵值為零、大小為 n 的 Jordan block 相似。
當 switch = 1,C 是非奇異(nonsingular)且良好狀況的(well-conditioned),並且其特徵值具有負實部。
Chebyshev spectral differentiation 矩陣的特徵向量矩陣 V 是不良狀況的(ill-conditioned)。
chebvand--Vandermonde-like matrix for the Chebyshev polynomials
C = gallery('chebvand',p)
產生以點向量 p 為起點的 (primal) Chebyshev Vandermonde 矩陣。p 定義 Chebyshev polynomial 從何計算。
C = gallery('chebvand',m,p)
m 是一個純量,產生上列矩陣的長方形版本,具有 m 列。
若 p 是向量,則: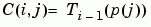 ,
,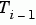 是冪次為
是冪次為 i-1 的 Chebyshev polynomial。若 p 是純量,則 p 為均勻分佈於 [0,1] 之間的點所形成的向量,以用來計算 C。
chow--Singular Toeplitz lower Hessenberg 矩陣
A = gallery('chow',n,alpha,delta)
回傳 A,此 A = H(alpha) + delta*eye(n),
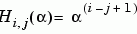 和
和 n 是 Chow 矩陣的階次。alpha、delta 是純量,初始值各為 1 及 0。
H(alpha) 有 p = floor(n/2) 個為零的特徵值。其餘的特徵值為 4*alpha*cos(k*pi/(n+2))^2,k=1:n-p。
circul--Circulant 矩陣
C = gallery('circul',v)
回傳 circulant 矩陣,第一列為向量 v。
circulant 矩陣的每一列都是由上一列元素循環排列而來。它是特別的 Toeplitz 矩陣,其對角線捲上(wrap around)。
若 v 是純量,則 C = gallery('circul',1:v)。
C (n x n)的特徵系統:若 t 是 n 次根,則 v 與 w = [1 t t2 ... t(n-1)] 的內積是 C 的特徵值,而 w(n:-1:1) 是特徵向量。
clement--對角線元素值為零的三角矩陣
A = gallery('clement',n,sym)
回傳一個 n x n 的三角矩陣,在主對角線上的元素和已知的特徵值為零。若 n 為奇數,則矩陣為奇異的(singular)。反矩陣的元素約有 64% 為零。特徵值不但包含 n-1, n-3, n-5, ... 的正負數,而且最後一個特徵值非 1 即 0 (當 n 為奇數時)。
sym 決定 Clement 矩陣是否為對稱矩陣。當 sym = 0 (預設值),矩陣非對稱;sym = 1,矩陣為對稱。
compar--對照矩陣
A = gallery('compar',A,1)
回傳 A,對角線上元素被本身的絕對值取代,而非對角線上的元素則減掉本列最大的絕對值。然而,若 A 是三角矩陣,compar(A,1) 也有相同的效果。
gallery('compar',A) 是 diag(B) - tril(B,-1) - triu(B,1),B = abs(A)。compar(A) 常被表示為 M(A)。
gallery('compar',A,0) 與 compar(A) 同。
condex--Counter-examples to matrix condition number estimators
A = gallery('condex',n,k,theta)
回傳 "counter-example" 矩陣的相容估計量(condition estimator)。矩陣具有階次 n 和純量參數 theta (預設值為 100)。
k = 1 |
4-by-4 |
LINPACK (rcond) |
k = 2 |
3-by-3 |
LINPACK (rcond) |
k = 3 |
arbitrary |
LINPACK (rcond) (independent of theta) |
k = 4 |
n 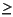 4 4 |
SONEST (Higham 1988) (default) |
若 n 與矩陣的自然大小不同,則矩陣由 n 階單位矩陣填滿。
cycol--行向量週期性重覆的矩陣
A = gallery('cycol',[m n],k)
回傳一個行向量週期性重覆的 m x n 矩陣,週期中的行向量由 randn(m,k) 產生。因此,矩陣 A 的稚不可超過 k。k 須為純量。
A = gallery('cycol',n,k),
n 是一個純量。此式與下列相同:gallery('cycol',[n n],k)。
dorr--對角線元素值較大、狀況不良的三角矩陣
[c,d,e] = gallery('dorr',n,theta)
回傳向量,這些向量定義了一個對角線元素值較大、階次為 n 的三角矩陣。此矩陣因由一些非負的微小數值 theta構成而狀況不良。theta 的預設值為 0.01。Dorr 矩陣本身與 gallery('tridiag',c,d,e) 相同。
A = gallery('dorr',n,theta)
回傳矩陣本身,而非定義的向量。
dramadah--由 0 與 1 構成的矩陣,但其反矩陣具有較大的元素值
A = gallery('dramadah',n,k)
回傳一個由 0 與 1 構成的 n x n 矩陣,其中 mu(A) = norm(inv(A),'fro') 具有相對較大但不一定為最大的值。Anti-Hadamard matrix A 是一個由 0 與 1 構成的矩陣,但其 mu(A) 是最大的。
fiedler--對稱的矩陣
A = gallery('fiedler',c),
c 是一個長度為 n 的向量,回傳一個 n x n 的對稱矩陣,其元素值為 abs(n(i)-n(j))。若 c 為純量,A = gallery('fiedler',1:c)。
inv(A) 與 det(A) 的詳細運算式可參見 [Todd, J., Basic Numerical Mathematics, Vol. 2: Numerical Algebra, Birkhauser, Basel, and Academic Press, New York, 1977, p. 159] 為 Fiedler 所做。由參考資料可知 inv(A) 為三角矩陣,除了非零的 (1,n) 與 (n,1) 元素。
forsythe--Perturbed Jordan block
A = gallery('forsythe',n,alpha,lambda)
回傳一個 n x n 矩陣,等同於特徵值為 lambda 的 Jordan block,除了 A(n,1) = alpha。純量 alpha 和 lambda 的預設值為 sqrt(eps)、0。
A 的特徵多項式(characteristic polynomial):
det(A-t*I) = (lambda-t)^N - alpha*(-1)^n.
frank--具有不良特徵根(ill-conditioned eigenvalues)的矩陣
F = gallery('frank',n,k)
回傳一個 n 階次的 Frank 矩陣。它的 upper Hessenberg 具有行列式值 1。若 k = 1,反對角線上的元素 (1,n)--(n,1) 受到影響。就 the zeros of the Hermite polynomials 來說,F 的特徵根可能存在。它們是正數,並且互為倒數成對出現;因此當 n 為奇數時,1 是一個特徵根。F 有 floor(n/2) 個較小的不良特徵值。
gearmat--Gear 矩陣
A = gallery('gearmat',n,i,j)
回傳 n x n 矩陣,在上、下對角線上的元素值為 1、在 (1,abs(i)) 上的元素值為 sign(i)、在 (n,n+1-abs(j)) 上的元素值為 sign(j),其他的元素值為0。參數 i、j的預設值為 n、-n。
矩陣 A 是奇異的,可以具有兩三倍的特徵值,可以是有缺陷的。
所有的特徵值都是像 2*cos(a) 這種形式,而特徵向量為 [sin(w+a), sin(w+2a), ..., sin(w+Na)],其中 a、w 由 Gear, C. W., "A Simple Set of Test Matrices for Eigenvalue Programs", Math. Comp., Vol. 23 (1969), pp. 119-125 給定。
grcar--具有敏感特徵值的 Toeplitz 矩陣
A = gallery('grcar',n,k)
回傳一個 n x n Toeplitz 矩陣,在下對角線上的元素為 -1、在對角線上的元素為 1、在 k 個上對角線上的元素為 1。k 預設為 3。特徵值是敏感的。
hanowa--特徵根在複數平面上呈垂直線分佈的矩陣
A = gallery('hanowa',n,d)
回傳由 n x n 個 2 x 2 矩陣構成的形式:
[d*eye(m) -diag(1:m) diag(1:m) d*eye(m)]
參數 n 是偶數 n=2*m。矩陣 A 有複數特徵根 d ± k*i,1 <= k <= m。d 預設為 -1。
house--Householder 矩陣
[v, beta] = gallery('house',x)
輸入 x,一個純量或是 n 個元素的行向量,然後回傳 v 與 beta 因而 eye(n,n) - beta*v*v' 是一個 Householder 矩陣。Householder 矩陣 H 滿足下列的關係:
H*x = -sign(x(1))*norm(x)*e1
e1 是 eye(n,n) 的第一行。注意,若 x 是複數,則 sign(x) = exp(i*arg(x))(相當於 x./abs(x) 當 x 不為零)。
invhess--upper Hessenberg 矩陣的反矩陣
A = gallery('invhess',x,y),
x 是長度為 n 的向量而 y 是長度為 n-1 的向量,回傳矩陣其下三角矩陣吻合 ones(n,1)*x' 而嚴格上三角矩陣吻合[1 y]*ones(1,n)。
若 x(1) ~= 0 且對所有 i,x(i+1) ~= y(i),加上反矩陣為 upper Hessenberg 矩陣,則此矩陣非奇異。參數 y 預設為 -x(1:n-1)。
若 x 是一個純量,invhess(x) 同於 invhess(1:x)。
invol--Involutory 矩陣
A = gallery('invol',n)
回傳一個 n x n involutory (A*A = eye(n)) 且不良狀況的矩陣。它是 hilb(n) 的對角線純量化版本。
B = (eye(n)-A)/2 且 B = (eye(n)+A)/2 是等冪的 (B*B = B)。
ipjfact--具有階乘元素的 Hankel 矩陣
[A,d] = gallery('ipjfact',n,k)
回傳 A、一個 n x n Hankel 矩陣、d(A 的行列式值)。若 k = 0 (預設),則 A 的元素為 A(i,j) = (i+j)!
若 k = 1,則 A 的元素為 A(i,j) = 1/(i+j)。
jordbloc--Jordan block
A = gallery('jordbloc',n,lambda)
回傳 n x n Jordan block,其特徵值為 lambda。lambda 的預設值為 1。
kahan--Upper trapezoidal 矩陣
A = gallery('kahan',n,theta,pert)
回傳一個 upper trapezoidal 矩陣,其相容估計量和稚的性質很有趣。
若 n 是兩個元素的向量,則 A 是 n(1) x n(2);否則,A 是 n x n。theta 的常用範圍介於 0 < theta < pi,預設值是 1.2。
為了確保有行向量交換的 QR 因數分解在進位捨去錯誤出現的時候沒有進行行向量交換,對角線被 pert*eps*diag([n:-1:1])擾亂。pert 預設為 25,如此確保在IEEE運算中,n 在 90 以上時,gallery('kahan',n) 沒有交換。
kms--Kac-Murdock-Szego Toeplitz 矩陣
A = gallery('kms',n,rho)
回傳 n x n Kac-Murdock-Szego Toeplitz 矩陣,其中 A(i,j) = rho^(abs(i-j)),對於實數 rho。
對於複數 rho,結果相同除了對角線下面的元素是共軛的。rho 預設為 0.5。
L = inv(triw(n,-rho,1)')、D(i,i) = (1-abs(rho)^2)*eye(n),除了 D(1,1) = 1 時。0 < abs(rho) < 1。inv(A) 是三角矩陣。krylov--Krylov 矩陣
B = gallery('krylov',A,x,j)
回傳 Krylov 矩陣
[x, Ax, A^2x, ..., A^(j-1)x]
其中 A 是一個 n x n 的矩陣而 x 是長度為 n 的向量。預設值是 x = ones(n,1),j = n。
B = gallery('krylov',n)
與 gallery('krylov',(randn(n)) 相同。
lauchli--矩形矩陣
A = gallery('lauchli',n,mu)
回傳 (n+1) x n 矩陣
[ones(1,n); mu*eye(n)]
Lauchli 矩陣在最小平方與其它指出 A'*A 的危險錯誤的問題中,是一個著名的例子。參數 mu 預設為 sqrt(eps)。
lehmer--對稱正定矩陣
A = gallery('lehmer',n)
回傳一個 n x n 的對稱正定矩陣,A(i,j) = i/j,對於 j >= i。
lesp--具有實數、敏感特徵根的三角矩陣
A = gallery('lesp',n)
回傳一個具有實數特徵根且均勻分佈於 [-2*N-3.5, -4.5] 區間的 n x n 矩陣。
當特徵根越負時,特徵根的敏感度會呈指數增加。這個矩陣與具有相同對角線元素和旁對角線元素為 1 的對稱三角矩陣相似,都是經由相似的轉換 D = diag(1!,2!,...,n!) 產生。
lotkin--Lotkin 矩陣
A = gallery('lotkin',n)
回傳第一列元素值都為 1 的 Hilbert 矩陣。Lotkin 矩陣 A 是非對稱的、不良狀況的,並且有許多較小負值的特徵根。它的反矩陣有明確的整數元素。
minij--對稱正定矩陣
A = gallery('minij',n)
回傳 n x n 的對稱正定矩陣,其中 A(i,j) = min(i,j)。
inv(A) 是三角矩陣且等於 -1 乘上 second difference 矩陣,除了它的 (n,n) 元素是 1。2*A-ones(size(A)),有三角反矩陣,且特徵根為 0.5*sec((2*r-1)*pi/(4*n))^2,其中 r=1:n。(n+1)*ones(size(A))-A 有元素為 max(i,j) 和三角反矩陣。moler--對稱正定矩陣
A = gallery('moler',n,alpha)
回傳 n x n 的對稱正定矩陣 U'*U,其中 U = triw(n,alpha)。
預設值 alpha = -1、A(i,j) = min(i,j)-2、A(i,i) = i。A 有一個較小的特徵根。
neumann--Singular matrix from the discrete Neumann problem(稀疏的)
C = gallery('neumann',n)
回傳奇異的、列對角線較大的矩陣,這個矩陣是由 discretizing the Neumann problem(在一般的 mesh 上使用 5 點運算子)而來。參數 n 是一個平方數
n = m2 或二元素向量。C 是稀疏的,並具有一維 null vector ones(n,1) 的 null space。
orthog--正交與近乎正交矩陣
Q = gallery('orthog',n,k)
回傳階次為 n 的第 k 型矩半,其中 k > 0 選擇絕對正交矩陣,k < 0 選擇正交矩陣的對角排列。矩陣類型如下:
parter--具有奇異值接近 pi 的 Toeplitz 矩陣
C = gallery('parter',n)
回傳矩陣 C,其中C(i,j) = 1/(i-j+0.5).
C 是一個 Cauchy 矩陣,也是 Toeplitz 矩陣。C 的大部份奇異值都很靠近 pi。
pei--Pei 矩陣
A = gallery('pei',n,alpha)
alpha 是一個純量,回傳對稱矩陣alpha*eye(n) + ones(n)。alpha 的預設值為 1。當 alpha 等於 0 或 -n 時,矩陣是奇異的。
poisson--Block tridiagonal matrix from Poisson's equation(稀疏的)
A = gallery('poisson',n)
回傳一個階次為 n^2 的 block tridiagonal 稀疏矩陣。這個矩陣是由 discretizing Poisson's equation(在 n x n mesh 上,使用 5 點運算子)而來。
prolate--對稱、不良狀況的 Toeplitz 矩陣
A = gallery('prolate',n,w)
回傳參數 w 的 n x n prolate 矩陣。它是對稱的 Toeplitz 矩陣。
randcolu - 具有標準化行向量與特定奇異值的隨機矩陣
A = gallery('randcolu',n)
是一個 n x n 的隨機矩陣,具有 unit 2-norm 的行向量與其平方值來自於 uniform distribution 的隨機奇異值。
A'*A 是一個由 gallery('randcorr',n) 產生的相關矩陣。
gallery('randcolu',x)
x 是一個 n-vector (n > 1), 產生一個 n x n 的隨機矩陣,它具有向量 x 給定的奇異值。向量 x 的元素非為負值,且所有元素的平方和為 n。
gallery('randcolu',x,m)
m >= n,產生 m x n 矩陣。
gallery('randcolu',x,m,k)
提供進階選項:
k = 0(預設)diag(x) 一開始進行隨機 two-sided orthogonal 轉換,然後一連串 Givens rotations 被套用。k = 1初始轉換被忽略。這更快,但產生的矩陣會有更多為零的元素。[1] Davies, P. I. and N. J. Higham, "Numerically Stable Generation of Correlation Matrices and Their Factors," BIT, Vol. 40, 2000, pp. 640-651.
randcorr - 具有特定特徵根的隨機相關矩陣
gallery('randcorr',n)
是一個具有從 uniform distribution 得到的隨機特徵根的 n x n 隨機相關矩陣。相關矩陣是對稱、半正定的矩陣,對角線上元素為 1。(見 corrcoef)。
gallery('randcorr',x)
產生一個隨機相關矩陣,其特徵根由向量 x 給定,length(x) > 1。向量 x 須具有總和為 length(x) 的非負值元素。
gallery('randcorr',x,k)
提供進階選項:
k = 0(預設)具有特徵根的三角矩陣一開始先進行隨機正交相似轉換(orthogonal similarity transformation),然後一連串 Givens rotations 被套用。k = 1初始轉換被忽略。這更快,但產生的矩陣會有更多為零的元素。[1] Bendel, R. B. and M. R. Mickey, "Population Correlation Matrices for Sampling Experiments," Commun. Statist. Simulation Comput., B7, 1978, pp. 163-182.
[2] Davies, P. I. and N. J. Higham, "Numerically Stable Generation of Correlation Matrices and Their Factors," BIT, Vol. 40, 2000, pp. 640-651.
randhess--隨機、正交 upper Hessenberg 矩陣
H = gallery('randhess',n)
回傳一個 n x n 實數、隨機、正交 upper Hessenberg 矩陣。
H = gallery('randhess',x)
若 x 是一個反覆無常、實數的、長度為 n 的向量(n > 1),使用 x 的元素當作參數來非隨機地產生 H。
矩陣 H 藉由 n-1 Givens rotations 的結果來產生。
rando--由元素 -1、0、1 構成的隨機矩陣
A = gallery('rando',n,k)
回傳一個 n x n 矩陣,其元素來自於下列非連續性的數值分佈:
k = 1 |
A(i,j) = 0 或 1,機率相同(預設)。 |
k = 2 |
A(i,j) = -1 或 1,機率相同。 |
k = 3 |
A(i,j) = -1、0、1,機率相同。 |
參數 n 可能是具有兩元素的向量,在這種情形下,回傳 n(1) x n(2) 矩陣。
randsvd--事先指定奇異值的隨機矩陣
A = gallery('randsvd',n,kappa,mode,kl,ku)
回傳一個階次為 n 的帶狀(多對角線)的隨機矩陣,其 cond(A) = kappa 且奇異值由分佈模式得到。若 n 是二元素向量,則 A 是 n(1) x n(2)。
參數 kl 和 ku 指定 A 中下、上旁對角線(off-diagonals)的數目。若被忽略,則產生一個完產的矩陣。若只有 kl 被指定,則 ku 預設為 kl。
1 |
一個大奇異值。 |
2 |
一個小奇異值。 |
3 |
幾何分佈奇異值(預設)。 |
4 |
標準常態分佈奇異值。 |
5 |
對數均勻分佈的隨機奇異值。 |
< 0 |
若模式是 -1、-2、-3、-4或-5,則 randsvd 把它們當作 abs(mode) 模式,除非在原本矩陣對角線上元素的順序是相反的:由小到大,而非由大到小。 |
Condition number kappa 預設為 sqrt(1/eps)。在特殊情形下 kappa < 0,A 是一個隨機、完整、對稱、正定矩陣,其中 cond(A) = -kappa 且特徵根依據模式分佈。忽略指定的參數 kl、ku。
redheff--由 1、0 組成的 Redheffer's 矩陣
A = gallery('redheff',n)
回傳一個由 0、1 組成的 n x n 矩陣,其中若 j = 1 或 i 整除 j,則 A(i,j) = 1;其他,A(i,j) = 0。
(n-floor(log2(n)))-1 特徵根為 1 sqrt(n)-sqrt(n)det(A) = O(n^(1/2+epsilon)),對每一個 epsilon > 0。Barrett 與 Jarvis 推測「較小的特徵根存在於單位圓 abs(Z) = 1 內」。這個推測的證明與「當 n 趨近無窮大時,某些特徵根會趨近零」的證明,都同意新的質數定理(prime number theorem)證明。
riemann--與 Riemann 假設相關的矩陣
A = gallery('riemann',n)
回傳一個 n x n 的矩陣,其中 Riemann 假設成立,若且唯若 det(A) = O(n! n^(-1/2+epsilon)),對每一個 epsilon > 0。
A = B(2:n+1,2:n+1)
若 i 整除 j,B(i,j) = i-1;其他,B(i,j) = -1。
e(i) 滿足 abs(e(i)) <= m-1/m,m = n+1。i <= e(i) <= i+1,最多 m-sqrt(m) 個例外。(m/3, m/2] 區間的所有整數都是特徵根。ris--對稱的 Hankel 矩陣
A = gallery('ris',n)
回傳一個對稱的 n x n Hankel 矩陣,其元素
A(i,j) = 0.5/(n-i-j+1.5)
A 的特徵根集中分佈於 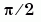 和
和 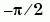 附近。這個矩陣是由 F.N. Ris 所提出。
附近。這個矩陣是由 F.N. Ris 所提出。
rosser--典型對稱特徵根測試矩陣
A = rosser
回傳 Rosser 矩陣。此矩陣對很多矩陣特徵根理論而言是一個挑戰。但是 Francis QR 理論,由 Wilkinson 使臻完美並實作在 MATLAB 上,則無此困擾。這個矩陣是具有整數元素的 8 x 8 矩陣,它有:
smoke--具有 'smoke ring' pseudospectrum 的複數矩陣
A = gallery('smoke',n)
回傳一個 n x n 矩陣,在上對角線上的元素為 1、在 (n,1) 位置上的元素為 1、沿著對角線的元素為 unity 的根的次方。
A = gallery('smoke',n,1)
回傳相同的矩陣,除了 A(n,1) 的元素為零。
smoke(n,1) 的特徵根為 unity 的 n 次方根;那些 smoke(n) 是 unity 的 n 次方根乘上 2^(1/n)。
toeppd--對稱正定 Toeplitz 矩陣
A = gallery('toeppd',n,m,w,theta)
回傳一個 n x n 對稱、半正定(SPD) Toeplitz 矩陣,由 m 個 rank 2(或某些 theta,rank 1)SPD Toeplitz 矩陣的和所構成。具體地,
T = w(1)*T(theta(1)) + ... + w(m)*T(theta(m))
其中 T(theta(k)) 有 (i,j) 元素 cos(2*pi*theta(k)*(i-j))。
預設:m = n、w = rand(m,1)、theta = rand(m,1)。
toeppen--五對角線 Toeplitz 矩陣(稀疏的)
P = gallery('toeppen',n,a,b,c,d,e)
回傳 n x n 的稀疏、五對角線 Toeplitz 矩陣,其對角線:P(3,1) = a、P(2,1) = b、P(1,1) = c、P(1,2) = d、P(1,3) = e,其中 a、b、c、d、e是純量。
預設 (a,b,c,d,e) = (1,-10,0,10,1),同於 Rutishauser 矩陣。這個矩陣的特徵根幾乎分佈於線段 2*cos(2*t) + 20*i*sin(t) 上。
tridiag--三角矩陣(稀疏的)
A = gallery('tridiag',c,d,e)
回傳下對角線 c、對角線 d、上對角線 e 的三角矩陣。向量 c、e 必須具有 length(d)-1。
A = gallery('tridiag',n,c,d,e),
其中 c、d、e 都是純量,同於 n 階的 Toeplitz 三角矩陣,下對角線元素 c、對角線元素 d、上對角線元素 e。此矩陣有特徵根。
d + 2*sqrt(c*e)*cos(k*pi/(n+1))
A = gallery('tridiag',n)
同於 A = gallery('tridiag',n,-1,2,-1),對稱正定的 M 矩陣(second difference 矩陣的負數版)。
triw--Wilkinson 和其他人所提出的上三角矩陣
A = gallery('triw',n,alpha,k)
回傳上三角矩陣,對角線元素為 1、前 k >= 0 個上對角線元素為 alpha。
階次 n 可能為 2-vector,此時矩陣為 n(1) x n(2) 且 upper trapezoidal。
Ostrowski ["On the Spectrum of a One-parametric Family of Matrices, J. Reine Angew. Math., 1954] 顯示
cond(gallery('triw',n,2)) = cot(pi/(4*n))^2,
並且大 abs(alpha)、cond(gallery('triw',n,alpha)) 幾乎是 abs(alpha)^n*sin(pi/(4*n-2))。
將 -2^(2-n) 加到 (n,1) 元素使得 triw(n) 為奇異,因此將 -2^(1-n) 加到第一行的所有元素上。
vander--Vandermonde 矩陣
A = gallery('vander',c)
回傳 Vandermonde 矩陣,其中第二個到最後一個行向量為 c。Vandermonde 矩陣的第 j 行由 A(:,j) = C^(n-j) 給定。
wathen--有限元素矩陣(稀疏、隨機的元素)
A = gallery('wathen',nx,ny)
回傳一個稀疏、隨機的 n x n 有限元素矩陣,其中
n = 3*nx*ny + 2*nx + 2*ny + 1。
對於在二度空間內的 nx-by-ny 格子(有八個頂點),矩陣 A 是 consistent mass 矩陣。對每一個在運算中隨機選擇的(正)密度 rho(nx,ny) 而言,A 是對稱的、正定的。
A = gallery('wathen',nx,ny,1)
回傳一個對角純量化的矩陣,其中
0.25 <= eig(inv(D)*A) <= 4.5
對於任何正整數的 nx、ny 與任何密度 rho(nx,ny),D = diag(diag(A))。
wilk--Wilkinson 提出的各種矩陣
[A,b] = gallery('wilk',n)
依據 n 而回傳不同的矩陣或線性系統:
See Also
hadamard, hilb, invhilb, magic, wilkinson
References
MATLAB 測試矩陣 gallery 是基於 Nicholas J. Higham at the Department of Mathematics, University of Manchester, Manchester, England 的研究。有關這些矩陣更深入的細節記載於文件 The Test Matrix Toolbox for MATLAB by N. J. Higham, September, 1995 中。這份報告在 MathWorks 的 ftp 站也可以取得 ftp://ftp.mathworks.com/pub/contrib/linalg/testmatrix/testmatrix.ps 或是在網站上 ftp://ftp.ma.man.ac.uk/pub/narep 或 http://www.ma.man.ac.uk/MCCM/MCCM.html。背景知識可以在這本書中發現 Accuracy and Stability of Numerical Algorithms, Nicholas J. Higham, SIAM, 1996。
 | fzero | gamma, gammainc, gammaln |  |