cgs (MATLAB Function Reference)

(translator=roro, ChineseSource=roro-20020630-8\cgs.html, EnglishSource=c:\matlabr12\help\techdoc\ref\cgs.html)

共軛梯度平方（Conjugate Gradients Squared）法

Syntax

x = cgs(A,b)
cgs(A,b,tol)
cgs(A,b,tol,maxit)
cgs(A,b,tol,maxit,M)
cgs(A,b,tol,maxit,M1,M2)
cgs(A,b,tol,maxit,M1,M2,x0)
cgs(afun,b,tol,maxit,m1fun,m2fun,x0,p1,p2,...)
[x,flag] = cgs(A,b,...)
[x,flag,relres] = cgs(A,b,...)
[x,flag,relres,iter] = cgs(A,b,...)
[x,flag,relres,iter,resvec] = cgs(A,b,...)

Description

x = cgs(A,b) 解線性方程式 A*x = b 的 x。A 為 n*n 的係數矩陣而行向量 b 的長度也必須為 n。A 可為函數 afun 且 afun(x) 回傳 A*x。

若 cgs 收歛，相關訊息將顯示出來。若 cgs 經過最大次數的重覆或任何理由被停止以致於沒有收歛，將會列印出一警告訊息顯示相關剩餘 norm(b-A*x)/norm(b)，而該作法下的重覆數字也將停止。

cgs(A,b,tol) 定義方法的誤差。若 tol 為 []，則 cgs 使用預設值 1e-6。

cgs(A,b,tol,maxit) 定義最大重覆次數。若 maxit 為 []，則 cgs 使用預設值 min(n,20)。

cgs(A,b,tol,maxit,M) 及 cgs(A,b,tol,maxit,M1,M2) 使用先決條件 M 或 M = M1*M2 並有效地解方程式 inv(M)*A*x = inv(M)*b 的 x。若 M 為 []，則 cgs 不使用任何先決控制條件。M 可為函式 mfun 其可回傳 M\x。

cgs(A,b,tol,maxit,M1,M2,x0) 定義初始的推測。若 x0 為 []，則 cgs 使用預設值。即全為零的向量。

cgs(afun,b,tol,maxit,m1fun,m2fun,x0,p1,p2,...) 傳送參數 p1,p2,... 至函式 afun(x,p1,p2,...), m1fun(x,p1,p2,...), 和 m2fun(x,p1,p2,...)

[x,flag] = cgs(A,b,...) 回傳 cgs 的解 x 及收歛旗標。

旗標
收歛性

0
bicgstab 在 maxit 次內收歛至期望的誤差 tol。

1
bicgstab 重覆 maxit 次但並沒有收歛。

2
先決條件 M 不夠完善。

3
bicgstab 沉滯（stagnated）。（兩次連續的重覆視為相同）。

4

經 bicgstab 計算的數值變得太小或太大以致於沒辦法繼續做計算。

旗標	收歛性
`0`	`bicgstab` 在 `maxit` 次內收歛至期望的誤差 `tol。`
`1`	`bicgstab` 重覆 `maxit` 次但並沒有收歛。
`2`	先決條件 `M` 不夠完善。
`3`	`bicgstab` 沉滯（stagnated）。（兩次連續的重覆視為相同）。
`4`	經 `bicgstab` 計算的數值變得太小或太大以致於沒辦法繼續做計算。

當 flag 不為 0 時，解 x 回傳經由所有重覆次數的最小基準餘數（minimal norm residual）。若有定義 flag 的輸出，則不會顯示任何訊息。

[x,flag,relres] = cgs(A,b,...) 亦回傳相關剩餘 norm(b-A*x)/norm(b)。若 flag 為 0, relres 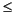tol。

[x,flag,relres,iter] = cgs(A,b,...) 亦回傳 x 計算時的重覆次數，即 0 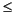iter 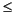maxit。

[x,flag,relres,iter,resvec] = cgs(A,b,...) 亦回傳在每一次重覆的剩餘基準估計向量，包括 norm(b-A*x0)。

Examples

範例 1

A = gallery('wilk',21);
b = sum(A,2);
tol = 1e-12;  maxit = 15; 
M1 = diag([10:-1:1 1 1:10]);
x = cgs(A,b,tol,maxit,M1,[],[]);

另外選擇使用矩陣向量乘法的函式

function y = afun(x,n)
y = [ 0; 
      x(1:n-1)] + [((n-1)/2:-1:0)'; 
      (1:(n-1)/2)'] .*x + [x(2:n); 
      0 ];

及先決反解（preconditioner backsolve）函式

function y = mfun(r,n)
y = r ./ [((n-1)/2:-1:1)'; 1; (1:(n-1)/2)'];

如同 cgs 的輸入。

x1 = cgs(@afun,b,tol,maxit,@mfun,[],[],21);

注意 afun 和 mfun 皆必須接收 cgs 額外的輸入 n=21。

範例 2

load west0479
A = west0479
b = sum(A,2)
[x,flag] = cgs(A,b)

flag 為 1 因為 cgs 經預設的 20 次重覆後沒有收歛。

[L1,U1] = luinc(A,1e-5)
[x1,flag1] = cgs(A,b,1e-6,20,L1,U1)

flag1 為 2 因為上三角 U1 在其對角線有一個零。此方法在第一次重覆去使用反斜線解方程式 U1*y = r 時會失敗。

[L2,U2] = luinc(A,1e-6)
[x2,flag2,relres2,iter2,resvec2] = cgs(A,b,1e-15,10,L2,U2)

flag2 為 0 因為當以微誤差為 1e-6 的前提下使用不完全 LU 分解在第五次重覆（iter2 的值）時 cgs 收歛值誤差值 6.344e-16 （relres2 的值）。resvec2(1) = norm(b) 且 resvec2(6) = norm(b-A*x2)。可藉由繪製 cgs 在每一次重覆相關剩餘的過程了解。

semilogy(0:iter2,resvec2/norm(b),'-o')
xlabel('iteration number')
ylabel('relative residual')

See Also

bicg, bicgstab, gmres, lsqr, luinc, minres, pcg, qmr, symmlq

@ (function handle), \ (backslash)

References

[1] Barrett, R., M. Berry, T. F. Chan, et al., Templates for the Solution of Linear Systems: Building Blocks for Iterative Methods, SIAM, Philadelphia, 1994.

[2] Sonneveld, Peter, "CGS: A fast Lanczos-type solver for nonsymmetric linear systems", SIAM J. Sci. Stat. Comput., January 1989, Vol. 10, No. 1, pp. 36-52.

cellstr 　 char