

| MATLAB Function Reference |   |
Syntax
[Q1,R1] = qrupdate(Q,R,u,v)
Description
[Q1,R1] = qrupdate(Q,R,u,v)
當 [Q,R] = qr(A) 為原先對 A 的 QR
分解,回傳 A + u*v' 的 QR 分解, u 和 v 為適當長度的行向量。
Remarks
qrupdate 僅對全矩陣(full matrices)作用。
Examples
mu = sqrt(eps) mu = 1.4901e-08 A = [ones(1,4); mu*eye(4)];
[Q,R] = qr(A);
R =
-1.0000 -1.0000 -1.0000 -1.0000
0 0.0000 0.0000 0.0000
0 0 0.0000 0.0000
0 0 0 0.0000
0 0 0 0
在此狀況中,上三角矩陣 R,不包括第一列,依序為 sqrt(eps)。
u = [-1 0 0 0 0]'; v = ones(4,1);
[QT,RT] = qr(A + u*v')
QT =
0 0 0 0 1
-1 0 0 0 0
0 -1 0 0 0
0 0 -1 0 0
0 0 0 -1 0
RT =
1.0e-007 *
-0.1490 0 0 0
0 -0.1490 0 0
0 0 -0.1490 0
0 0 0 -0.1490
0 0 0 0
[Q1,R1] = qrupdate(Q,R,u,v)
Q1 =
-0.0000 -0.0000 -0.0000 -0.0000 1.0000
1.0000 -0.0000 -0.0000 -0.0000 0.0000
0.0000 1.0000 -0.0000 -0.0000 0.0000
0.0000 0.0000 1.0000 -0.0000 0.0000
-0.0000 -0.0000 -0.0000 1.0000 0.0000
R1 =
1.0e-007 *
0.1490 0.0000 0.0000 0.0000
0 0.1490 0.0000 0.0000
0 0 0.1490 0.0000
0 0 0 0.1490
0 0 0 0
Algorithm
qrupdate 使用的演算法在 Matrix Computations(作者為 Golub
及 van Loan)第三版的 12.5.1 節,若我們取 N = max(m,n),則使用一新的 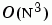 演算法做 QR 分解,藉由此方法簡易地更新已存在的因子為
演算法做 QR 分解,藉由此方法簡易地更新已存在的因子為 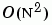 演算法。
演算法。
References
Golub, Gene H. and Charles Van Loan, Matrix Computations, Third Edition, Johns Hopkins University Press, Baltimore, 1996
See Also
 | qrinsert | quad, quad8 |  |