MATLAB Function Reference

quad, quad8

以 adaptive Simpson quadrature 求積分的值

Note    用較高等方法寫成的 quad8 函數已經廢棄不用了。quadl 函數是建議的替代函數。

Syntax

q = quad(fun,a,b)
q = quad(fun,a,b,tol)
q = quad(fun,a,b,tol,trace)
q = quad(fun,a,b,tol,trace,p1,p2,...)
[q,fcnt] = quadl(fun,a,b,...)

Description

Quadrature 是一個用來找函數圖形下方面積的數值方法，就是計算定積分的方法。

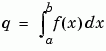
q = quad(fun,a,b) 以 recursive adaptive Simpson quadrature 求函數 fun 從 a 到 b 定積分的近似值，誤差在 10^-6 之內。fun 接受一個向量 x 而傳回一個向量 y，函數 fun 對 x 的每個元素求值。

q = quad(fun,a,b,tol) 用一個特定的誤差容忍值 tol 取代預設值 1.0e-6。較大的 tol 會有較少的函數運算和較快的計算，不過答案較不準確。在 MATLAB 5.3 和較早的版本中，quad 函數使用較不可信賴的演算法且預設的誤差容忍值是 1.0e-3。

q = quad(fun,a,b,tol,trace) 以非零的 trace 會在遞迴運算中顯示出 [fcnt a b-a Q] 的值。

q = quad(fun,a,b,tol,trace,p1,p2,...) 提供多餘的參數 p1,p2,... 直接傳遞到函數 fun 中，fun(x,p1,p2,...)。在 tol 或 trace 傳入空矩陣可以使用預設值。

[q,fcnt] = quad(...) 傳回函數的計算次數。

quadl 函數在計算高準確度和平滑的被積函數(integrand)時，會效率較高。

Examples

你可以用三種不同的方法定義 fun ：

• 只有一個變數的字串表示法

Q = quad('1./(x.^3-2*x-5)',0,2); 

• inline 物件

F = inline('1./(x.^3-2*x-5)'); 
Q = quad(F,0,2); 

• 用函數處理

Q = quad(@myfun,0,2); 

其中 myfun.m 是一個 M-file。

function y = myfun(x) 
y = 1./(x.^3-2*x-5);

Algorithm

quad 使用 adaptive recursive Simpson's rule 建構一個低等級的方法。

Diagnostics

quad 可能發出下列其中一個警告：

'Minimum step size reached' 表示原來間距在間距遞迴分枝時，已經產生一個距離在捨去誤差等級的間距。可能產生不完整的罕見錯誤。

'Maximum function count exceeded' 表示被積函數(integrand)已經被計算超過 10,000 次。可能產生不完整的罕見錯誤。

'Infinite or Not-a-Number function value encountered' 表示在被積函數(intrgrand)間距中的計算中產生浮點數溢位或是除以零。

See Also

dblquad, inline, quadl, @ (function handle)

References

[1]  Gander, W. and W. Gautschi, "Adaptive Quadrature - Revisited", BIT, Vol. 40, 2000, pp. 84-101. This document is also available at http://www.inf.ethz.ch/personal/gander.

qrupdate

quadl