

| MATLAB Function Reference |   |
Syntax
[Q,R] = qr(A) [Q,R,E] = qr(A) [Q,R] = qr(A,0) [Q,R,E] = qr(A,0) R = qr(A) (sparse matrices) [C,R] = qr(A,B) (sparse matrices) R = qr(A,0) (sparse matrices) [C,R] = qr(A,B,0) (sparse matrices) X = qr(A)
Description
函式 qr
對矩陣作直角三角分解。此分解法對正方及長方矩陣皆有效。原本矩陣以一實數直角或複數單一矩陣及一上三角矩陣的乘積來表示。
[Q,R] = qr(A)
產生一維度等同於 A 的上三角矩陣 R 及一元矩陣 Q,關係式為 A = Q*R。若為稀疏矩陣,則 Q
通常近於填滿的(full)。
[Q,R,E] = qr(A)
產生一排列矩陣 E,一含有遞降對角線元素的上三角矩陣 R,及一元矩陣 Q,其關係式為 A*E = Q*R。會使 abs(diag(R))
產生最小值的行排列矩陣 E 將被選擇。
[Q,R] = qr(A,0) and [Q,R,E] = qr(A,0)
產生經濟尺寸(economy-size)分解,E 為一排列向量,其關係式為 Q*R = A(:,E)。會使 abs(diag(R))
產生最小值的行排列矩陣 E 將被選擇。
R = qr(A)
對稀疏矩陣而言,僅產生一上三角矩陣 R。矩陣 R
提供了 Cholesky 分解法對相關矩陣做運算,
R'*R = A'*A
[C,R] = qr(A,B)
對於稀疏矩陣提供對 B 做垂直轉換,產生 C = Q'*B
而不用先計算出 Q。
R = qr(A,0) and [C,R] = qr(A,B,0)
對於稀疏矩陣產生經濟尺寸(economy-size)結果。
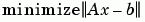
[C,R] = qr(A,b) x = R\c
若 A 為稀疏矩陣但不為正方矩陣,MATLAB
使用上述的兩步驟對其線性方程式解反斜線運算元,即 x = A\b。
X = qr(A)
回傳 LAPACK 子程序 DGEQRF
或 ZGEQRF 的輸出。triu(qr(A)) 為 R。
Examples
A =
1 2 3
4 5 6
7 8 9
10 11 12
[Q,R] = qr(A)
Q =
-0.0776 -0.8331 0.5444 0.0605
-0.3105 -0.4512 -0.7709 0.3251
-0.5433 -0.0694 -0.0913 -0.8317
-0.7762 0.3124 0.3178 0.4461
R =
-12.8841 -14.5916 -16.2992
0 -1.0413 -2.0826
0 0 0.0000
0 0 0
三角結構 R 將其零放置於對角線下;在對角線 R(3,3)
的零表示 R 及 A 並不是有全行列的(full rank)。
b =
1
3
5
7
線性系統 Ax = b 表示有四個方程式及三個未知數。對此問題的最佳解可藉由下式得到
x = A\b
Warning: Rank deficient, rank = 2, tol = 1.4594E-014
x =
0.5000
0
0.1667
tol 為誤差容忍度,其用來決定 R
的對角元素是否可忽略。若 [Q,R,E] = qr(A),則
tol=max(size(A))*eps*abs(R(1,1))
y = Q'*b;
x = R\y
計算的解可經由 Ax 檢查。b 有進位誤差,其代表即使模擬方程式 Ax = b
為過於決定(overdetermined)及行列定義(rank deficient),則含有一致性。若有無限多組向量解 x;則 QR
分解會選擇其中一項解。
Algorithm
| 語法 |
實數 |
複數 |
R = qr(A) |
DGEQRF |
ZGEQRF |
[Q,R] = qr(A) |
DGEQRF, DORGQR |
ZGEQRF, ZUNGQR |
| [Q,R,e] = qr(A) [Q,R,e] = qr(A,0) |
DGEQPF, DORGQR |
ZGEQPF, ZUNGQR |
See Also
lu, null, orth, qrdelete, qrinsert
The arithmetic operators \ and /
References
[1] Anderson, E., Z. Bai, C. Bischof, S. Blackford, J. Demmel, J. Dongarra, J. Du Croz, A. Greenbaum, S. Hammarling, A. McKenney, and D. Sorensen, LAPACK User's Guide, Third Edition, SIAM, Philadelphia, 1999.
 | qmr | qrdelete |  |