MATLAB Function Reference

gradient

數值梯度(Numerical gradient)

Syntax

FX = gradient(F)
[FX,FY] = gradient(F)
[Fx,Fy,Fz,...] = gradient(F)
[...] = gradient(F,h)
[...] = gradient(F,h1,h2,...)

Definition

有兩個變數的 gradient 函數，F(x,y)，定義如下：

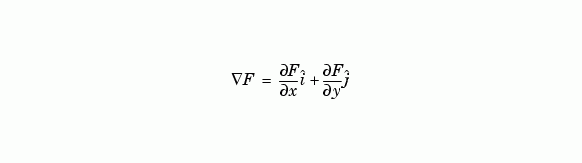
可以把它想成是在 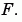增值方向向量點的聚集。在 MATLAB 裡，數值梯度(numerical gradients)(differences)可以計算任何變數個數的函數。對於一個 N 個變數的函數，F(x,y,z,...)，

Description

FX = gradient(F) 其中 F 是一個傳回 F 的一維數值梯度(numerical gradient)向量。FX 對應 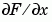，在 x 方向的差值。

[FX,FY] = gradient(F) 其中 F 是一個傳回二維梯度(numerical gradient)之 x 和 y 元件的矩陣。 FX 對應 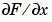， x (直行)方向的差值。 FY 對應 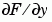，y (橫列)方向的差值。各個維度的間距被當成是一。

[FX,FY,FZ,...] = gradient(F) 其中 F 有 N 維度傳回 N 個 F 的梯度元件。有兩個方法來控制 F 各個值的間距：

• 一個單一的間距值，h，定義每個方向的間距。
• N 個間距值，(h1,h2,...)定義 F 各個維度的間距。純量的空間參數對每個維度定義一個常數空間。向量參數沿著 F 對應的維度定義座標的值。在這個狀況下，向量的長度必須和對應維的的大小吻合。

[...] = gradient(F,h) 其中 h 是一個純量，用 h 當作每個維度點的間距。

[...] = gradient(F,h1,h2,...) 空間參數 N 定義 F 各個維度的間距。

Examples

陳述式

v = -2:0.2:2;
[x,y] = meshgrid(v);
z = x .* exp(-x.^2 - y.^2);
[px,py] = gradient(z,.2,.2);
contour(v,v,z), hold on, quiver(px,py), hold off

產生

給定，

F(:,:,1) = magic(3); F(:,:,2) = pascal(3);
gradient(F) takes dx = dy = dz = 1.
[PX,PY,PZ] = gradient(F,0.2,0.1,0.2) takes dx = 0.2, dy = 0.1, and 
dz = 0.2.

See Also

del2, diff

gplot

graymon