

| MATLAB Function Reference |   |
Syntax
R1 = cholupdate(R,x) R1 = cholupdate(R,x,'+') R1 = cholupdate(R,x,'-') [R1,p] = cholupdate(R,x,'-')
Description
R1 = cholupdate(R,x)
R = chol(A) 為原本對 A 的 Cholesky
分解法,回傳一 A + x*x' 的上三角 Cholesky 因子,x 為適當長度的行向量。cholupdate
僅使用 R 的對角線及上三角部份,下三角部份將被忽略。
R1 = cholupdate(R,x,'+')
等同於 R1 = cholupdate(R,x)。
R1 = cholupdate(R,x,'-')
回傳 A - x*x' 的 Cholesky 因子。當 R 不是一合理的 Cholesky
因子或當 downdated 矩陣不是正向定義且沒有經 Cholesky factorization,則會印出錯誤訊息。
[R1,p] = cholupdate(R,x,'-')
不會回傳錯誤訊息。若 p 為 0,R1
為 A - x*x' 的 Cholesky 因子。若 p 大於 0,R1
為原本 A 的 Cholesky 因子。若 p 為 1,cholupdate
會因為 downdated 矩陣不為正向定義而無法運作。若 p 為 2,cholupdate
會因為 R 的上三角部份不為合理的 Cholesky 因子而無法運作。
Remarks
cholupdate 僅對全矩陣(full matrices)作用。
Example
A = pascal(4) A =
1 1 1 1
1 2 3 4
1 3 6 10
1 4 10 20
R = chol(A)
R =
1 1 1 1
0 1 2 3
0 0 1 3
0 0 0 1
x = [0 0 0 1]';
此稱為行列一更新成 A 既然 rank(x*x') 為 1:
A + x*x' ans =
1 1 1 1
1 2 3 4
1 3 6 10
1 4 10 21
使用 cholupdate 取代運用 R1 = chol(A + x*x')
計算 Cholesky 因子:
R1 = cholupdate(R,x) R1 =
1.0000 1.0000 1.0000 1.0000
0 1.0000 2.0000 3.0000
0 0 1.0000 3.0000
0 0 0 1.4142
而後藉由對 A 中最後一個元素減去 1 來使其沒有正向定義(positive definiteness)。該
downdated 矩陣為:
A - x*x' ans =
1 1 1 1
1 2 3 4
1 3 6 10
1 4 10 19
R1 = chol(A-x*x') ??? Error using ==> chol Matrix must be positive definite. R1 = cholupdate(R,x,'-') ??? Error using ==> cholupdate Downdated matrix must be positive definite.
然而,從 A 的最後一個元素減去 0.5
產生一正向定義矩陣,我們可使用 cholupdate 計算其 Cholesky 因子:
x = [0 0 0 1/sqrt(2)]';
R1 = cholupdate(R,x,'-')
R1 =
1.0000 1.0000 1.0000 1.0000
0 1.0000 2.0000 3.0000
0 0 1.0000 3.0000
0 0 0 0.7071
Algorithm
cholupdate 的演算法為使用 LINPACK 子程序 ZCHUD
及 ZCHDD。cholupdate 用於計算新的 Cholesky 因子,為一種 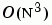 的演算法,並用此方法簡易地更新已存在的因子為一種
的演算法,並用此方法簡易地更新已存在的因子為一種 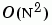 的演算法。
的演算法。
References
Dongarra, J.J., J.R. Bunch, C.B. Moler, and G.W. Stewart, LINPACK Users' Guide, SIAM, Philadelphia, 1979.
See Also
 | cholinc | cla |  |