

| MATLAB Function Reference |   |
Syntax
p = polyfit(x,y,n) [p,S] = polyfit(x,y,n) [p,S,mu] = polyfit(x,y,n)
Description
p = polyfit(x,y,n)
找尋 n 次多項式 p(x)
的係數其滿足從 p(x(i)) 至 y(i)。回傳的結果 p
為一長度為 n+1
的列向量其元素依降冪表示為多項式係數。
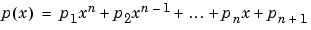
[p,S] = polyfit(x,y,n)
回傳多項式係數 p 及在函式 polyval
中使用的結構 S 存放誤差估計。若資料 y
輸入的錯誤獨立於常數變數,polyval 含有至少 50% 的準確性。
[p,S,mu] = polyfit(x,y,n)
找尋在下式中的多項式係數
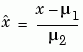
Examples
這個範例涉入了誤差的函式 erf(x) x
為多項式。這是一個不安全的範例,因為 erf(x)
是有界的函數,而多項式是無界的。
首先產生 x
個點的向量,等距的在一範圍 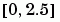 ;然後對這些點計算其
;然後對這些點計算其 erf(x)。
x = (0: 0.1: 2.5)'; y = erf(x);
p = polyfit(x,y,6)
p =
0.0084 -0.0983 0.4217 -0.7435 0.1471 1.1064 0.0004
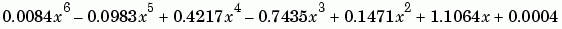
f = polyval(p,x);
table = [x y f y-f]
table =
0 0 0.0004 -0.0004
0.1000 0.1125 0.1119 0.0006
0.2000 0.2227 0.2223 0.0004
0.3000 0.3286 0.3287 -0.0001
0.4000 0.4284 0.4288 -0.0004
...
2.1000 0.9970 0.9969 0.0001
2.2000 0.9981 0.9982 -0.0001
2.3000 0.9989 0.9991 -0.0003
2.4000 0.9993 0.9995 -0.0002
2.5000 0.9996 0.9994 0.0002
故於此間距內,精確值在三到四位。在這間距後,誤差值將愈來愈大
x = (0: 0.1: 5)'; y = erf(x); f = polyval(p,x); plot(x,y,'o',x,f,'-') axis([0 5 0 2])
Algorithm
polyfit M 檔案形成 Vandermonde 矩陣 V,其元素為 x
的冪次。
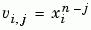
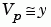
See Also
 | polyeig | polyint |  |