

| MATLAB Function Reference |   |
一維的快速傅利葉轉換(One-dimensional fast Fourier transform)
Syntax
Y = fft(X) Y = fft(X,n) Y = fft(X,[],dim) Y = fft(X,n,dim)
Definition
X = fft(x) 和 x = ifft(X) 函式會執行向量長度為 N 的轉換和反轉換:
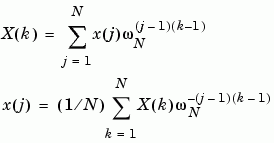

Description
Y = fft(X)
會傳回對向量 X 做快速傅利葉轉換後的值。
若 X 是一個矩陣, fft 會對矩陣的每一行來做傅利葉轉換。
若 X 是一個多維陣列, fft 會對矩陣的第一個維度來作處理。
Y = fft(X,n)
傳回 n 個點的 FFT。若 X 的長度小於 n,X 會在不足 n 的部分補 0。若 X 的長度大於 n,X 超過的部分會被截斷。當 X 是一個矩陣時,行的長度調整也是採相同的機制。
Y = fft(X,[],dim) 和 Y = fft(X,n,dim)
dim。
Examples
傅利葉轉換通常用在找尋時間域信號中,頻率的組成方式。假設一資料用 1000 Hz 取樣。建立一個包含 50 Hz 和 120 Hz ,且與 zero-mean random noise結合的信號:
t = 0:0.001:0.6;
x = sin(2*pi*50*t)+sin(2*pi*120*t);
y = x + 2*randn(size(t));
plot(y(1:50))
title('Signal Corrupted with Zero-Mean Random Noise')
xlabel('time (seconds)')
我們從原始信號中很難觀察出其頻率的組成,所以可以將信號轉換到頻率域中。以下的例子,信號 y 會做 512-point 的 fast Fourier transform (FFT):
Y = fft(y,512);
其功率頻譜(power spectrum),或稱做 measurement of the power at various frequencies,為下列:
Pyy = Y.* conj(Y) / 512;
描繪出前 257 個點 (其餘 255 個點都是多餘的) 在一特定的頻率軸上:
f = 1000*(0:256)/512;
plot(f,Pyy(1:257))
title('Frequency content of y')
xlabel('frequency (Hz)')
這表示 y 中頻率的內容會在 DC 的範圍中,且包含奈奎斯特頻率(Nyquist frequency) (即這個信號會產生很高的波峰)。
Algorithm
FFT 函式 (fft, fft2, fftn, ifft, ifft2, ifftn) 建立在 FFTW 的函式庫上[3],[4]。當 N 為合成(即 N = N1N2) ,為了要計算 N 個點的 DFT , FFTW 函式庫會用 Cooley-Tukey演算法來分解這個問題 [1]( 先算 N2 大小的 N1 轉換, 再算 N1 大小的 N2 轉換)。 N1- 和 N2-point DFTs 可以遞迴地分解直到這個問題可以被一些 machine-generated fixed-size 的方法所解決(codelets)。"codelets" 會依次結合一些演算法來使用,包括 Cooley-Tukey 的變動(variation)[5],質數分解的演算法,[6] split-radix 演算法 [2]。而 N 的分解是經由嘗試錯誤所得到的。
當 N 是一個質數時,FFTW 函式庫會先用 Rader's 演算法,來分解這個問題至三個 (N-1)-point 的問題 [7]。然後用 Cooley-Tukey 分解來計算 (N-1)-point DFTs。
對大多數的 N 來說,real-input DFTs 所需計算的的時間約為complex-input DFTs 的一半。然而當 N 有大的質因數時,則計算時間上將沒什麼差別。
執行 fft 所需的時間取決於轉換的長度,在二的次方時最快,當長度擁有小的質因數時也很快。而當長度為質數或擁有大的質因數時,會比較慢。
See Also
dftmtx, filter, 和 freqz 是在 Signal Processing Toolbox, and:
References
[1] Cooley, J. W. and J. W. Tukey, "An Algorithm for the Machine Computation of the Complex Fourier Series," Mathematics of Computation, Vol. 19, April 1965, pp. 297-301.
[2] Duhamel, P. and M. Vetterli, "Fast Fourier Transforms: A Tutorial Review and a State of the Art," Signal Processing, Vol. 19, April 1990, pp. 259-299.
[3] FFTW (http://www.fftw.org)
[4] Frigo, M. and S. G. Johnson, "FFTW: An Adaptive Software Architecture for the FFT," Proceedings of the International Conference on Acoustics, Speech, and Signal Processing, Vol. 3, 1998, pp. 1381-1384.
[5] Oppenheim, A. V. and R. W. Schafer, Discrete-Time Signal Processing, Prentice-Hall, 1989, p. 611.
[6] Oppenheim, A. V. and R. W. Schafer, Discrete-Time Signal Processing, Prentice-Hall, 1989, p. 619.
[7] Rader, C. M., "Discrete Fourier Transforms when the Number of Data Samples Is Prime," Proceedings of the IEEE, Vol. 56, June 1968, pp. 1107-1108.
 | feval | fft2 |  |