

| MATLAB Function Reference |   |
稀疏不完全 Cholesky 及無窮 Cholesky 分解法
Syntax
R = cholinc(X,droptol) R = cholinc(X,options) R = cholinc(X,'0') [R,p] = cholinc(X,'0') R = cholinc(X,'inf')
Description
cholinc 產生兩種不同的不完全 Cholesky 分解:微誤差和 0
層次的填滿分解法。這些因子對於使用如 pcg 的重覆方法所解的對稱正向定義的線素方程組可能為有用的先決條件。cholinc
僅針對稀疏矩陣作用。
R = cholinc(X,droptol)
使用微誤差 droptol 對 X 執行不完全 Cholesky
分解。
R = cholinc(X,options)
提供不完全 Cholesky 分解額外的選項。options
為一含有以下三個欄位的結構:
droptol |
不完全分解的微誤差 |
michol |
修改後的不完全 Cholesky |
rdiag |
取代 R 對角線上的零 |
droptol 為一非負數的數值用來表示不完全 Cholesky
分解的微誤差。此分解藉由執行軸臨界點為 0,而後以欄對角元素的平方根來放大縮小不完全上三角因子 U 的列之不完全 LU 分解來計算。非零元素 U(i,j)
由 droptol*norm(X(:,j)) 約束 (參考 luinc),而非零元素 R(i,j)
由局部微誤差 droptol*norm(X(:,j))/R(i,i) 來約束。
設定 droptol = 0 以產生完全 Cholesky 分解,其為預設值。
michol 表示已修飾後的不完全 Cholesky 分解。其值為 0 (未修飾過,即預設值)
或 1 (已修飾過)。其執行已修飾不完全 LU 分解的 X 並如同上述的縮放回傳的上三角因子。
rdiag 為 0 或 1。若其為 1,任何上三角因子 R
的對角線零元素收被局部誤差的平方根所取代,以避免最後結果為單一數值的因子。預設值為 0。
R = cholinc(X,'0')
產生一對稱且正向定義實數稀疏矩陣的不完全 Cholesky 因子。上三角 R
有著和 triu(X) 相同的稀疏結構,雖然 R 在一些 X
為非零而產生約分的情況下可能為零。下三角 X 假設成上三角的轉置。注意 X
的正向定義並不保証稀疏結構因子的存在。若無法執行分解,錯誤訊息將產生。若分解成功,R'*R 將對應於 X
的稀疏結構。
[R,p] = cholinc(X,'0')
有兩個輸出的參數,而不會產生錯誤訊息。若 R 存在,p
為 0。若 R 不存在, p 為正整數且 R 為一 q*n
且 q = p-1 的上三角矩陣。在這後一個狀況中,R
的稀疏結構為上三角 X 的 q*n 部份。R'*R 對應於 X
前 q 行及前 q 列的稀疏結構。
R = cholinc(X,'inf')
產生無窮 Cholesky 分解。此分解是以 Cholesky
分解為基礎,並額外地處理實數正向不完全定義(real positive semi-definite)矩陣。針對找出產生內部點的解很有用。當在原本的 Cholesky
分解中碰到軸心(pivot)為零時,無窮 Cholesky 的對角線因子將設為 Inf 而該列中其餘的元素將設定成 0。其於相關線性方程式系統中解答向量的對應元素強迫其為 0。X
被設為正向不完全定義故即使是負數的軸心也會被 Inf 所取代。
Remarks
以不完全分解為先決條件下解大型稀疏結構的線性方程式很有用。在上三角因子對角線上的 0
使其單一化。若上三角因子在其對角線有零,則含有微誤差的不完全分解將顯示警告訊息。同樣地,使用 rdiag
選項以取代零對角線僅不管問題的徵兆,但並沒有解決這個問題。先決條件可以不為單一,但不一定有用,而警告訊息也將列印出來。
無窮 Cholesky 分解法為使用內部點的方法。否則並不建議用它。
Example 1.
S = delsq(numgrid('C',15));
S 為二維矩陣,numgrid('C',15) 產生其五點不連續負數 Lapacian。
計算層級為 0 的 Cholesky 分解及不完全 Cholesky 分解比和填滿來做比較。
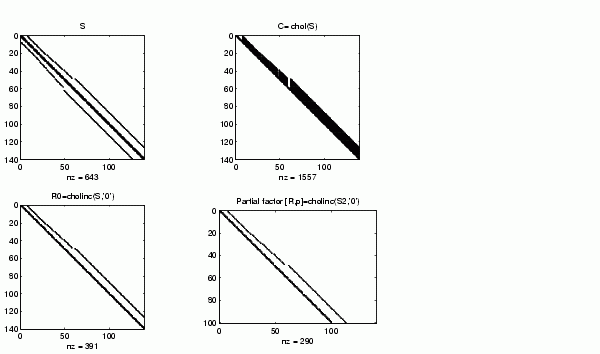
C = chol(S); R0 = cholinc(S,'0'); S2 = S; S2(101,101) = 0; [R,p] = cholinc(S2,'0');
填滿造成 S 在完全 Cholesky 因子中的嵌入,但並不在不完全 Cholesky
因子。單值 S2 的不完全分解停止於列 p = 101 並產生一 100*139 的不完全因子。
D1 = (R0'*R0).*spones(S)-S; D2 = (R'*R).*spones(S2)-S2;
D1 有 eps 次序的元素,顯示 R0'*R0
和 S 有相同的稀疏結構。D2 的元素在前 100 列及前 100 行,即 D2(1:100,:) and D2(:,1:100)
有 eps次序的元素。
Example 2.
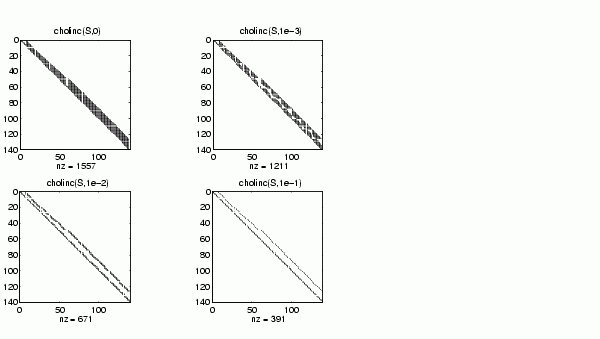
第一個平面圖顯示 cholinc(S,0),即微誤差為 0 的不完全 Cholesky
因子,其等同於 S 的 Cholesky 因子。不完全因子的稀疏結構將隨著微誤差的增加而增加,可由下圖得知。
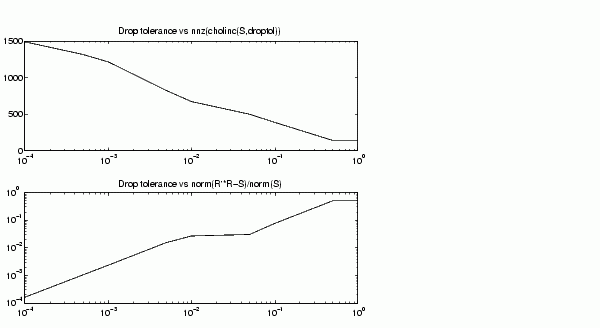
不幸地,稀疏因子為不充足的近似值,可由下圖微誤差對比於 norm(R'*R-S,1)/norm(S,1)
得知。
Example 3.
Hilbert 矩陣第 (i,j) 個元素為 1/(i+j-1) 且為正向定義:
H3 = hilb(3)
H3 =
1.0000 0.5000 0.3333
0.5000 0.3333 0.2500
0.3333 0.2500 0.2000
R3 = chol(H3)
R3 =
1.0000 0.5000 0.3333
0 0.2887 0.2887
0 0 0.0745
H20 = sparse(hilb(20));
[R,p] = chol(H20);
p =
14
For hilb(20),即 Cholesky 分解在計算第 14
列的時候失敗,起因於軸心為零。這時可由無窮 Cholesky 分解以避免錯誤。當遇到軸時為零時,cholinc 放置 Inf
至主對角線上,並繼續計算:
Rinf = cholinc(H20,'inf');
在這狀況下,所有的子序列軸心因為太小,所以剩餘的上三角因子為:
full(Rinf(14:end,14:end))
ans =
Inf 0 0 0 0 0 0
0 Inf 0 0 0 0 0
0 0 Inf 0 0 0 0
0 0 0 Inf 0 0 0
0 0 0 0 Inf 0 0
0 0 0 0 0 Inf 0
0 0 0 0 0 0 Inf
Limitations
cholinc 僅針對正方稀疏矩陣作用。cholinc(X,'0')
及 cholinc(X,'inf') 中的 X 必須為實數。
Algorithm
R = cholinc(X,droptol) 由 [L,U] = luinc(X,options)
產生,其中 options.droptol = droptol 且 options.thresh = 0。上三角 U
的列經由列的對角平方根縮放,而縮放因子變為 R。
R = cholinc(X,options) 在相似的方法下產生,除了 rdiag
選項轉變成 udiag 選項且 milu 選項取出 michol 的值。
R = cholinc(X,'0') 根據 Cholesky 分解中的 "KJI"
變數。唯有在定義上三角 X 的非零位置時才會更新。
R = cholinc(X,'inf') 以在 Zhang ([2])
的演算法為基礎。
See Also
References
[1] Saad, Yousef, Iterative Methods for Sparse Linear Systems, PWS Publishing Company, 1996, Chapter 10 - Preconditioning Techniques.
[2] Zhang, Yin, Solving Large-Scale Linear Programs by Interior-Point Methods Under the MATLAB Environment, Department of Mathematics and Statistics, University of Maryland Baltimore County, Technical Report TR96-01
 | chol | cholupdate |  |