9-2 Discrete HMM

Old Chinese version

The simplest ASR application is voice command recognition. To construct a voice command recognizer, we need to collect training data for each voice command. This data is used for constructing an HMM for each voice command. For a given utterance, we need to send the corresponding acoustic features (MFCC, for example) to each HMM for evaluation the log probability. The HMM with the highest log probability represents the predicted voice command for the given utterance.

For simplicity in the following discussion, we shall assume our goal is to construct a speaker-independent digit recognizer that can recognize the utterance of 0 ~ 9. There are two steps involved in the design of such recognition system:

1. Corpus collection: To achieve speaker independence, we need to have a wide collection of speech corpus, including:
   • Subjects: We need to have utterances from various subjects, including different genders, different age groups, different accent (from different regions), etc.
   • Recording devices: We need to use different microphones and different sound cards, etc.
   • Environment: We need to have a recording environment that is close to that of the recognizer at application. To increase the robustness of the trained acoustic models, we should do the recording at quiet locations such as labs/offices, as well as noisy locations such as restaurants and road sides, etc.
2. Recognizer design: We need to design a recognizer based on HMM and test its performance. This will be detailed in the rest of this section.

First of all, we need to construct a DHMM for each digit. Take the digit 「九」for example, the corresponding DHMM is shown next: In other words, we can segment the utterance of 「九」into 3 states, each representing the pronunciation of ㄐ, ㄧ, ㄡ. Note that each state covers a few frames, and the degree to which a frame belongs to a state is specified by a state probability. Moreover, for a given frame, it can stay in the current state with a self-transition probability, or transit to the next state with a next-transition probability.

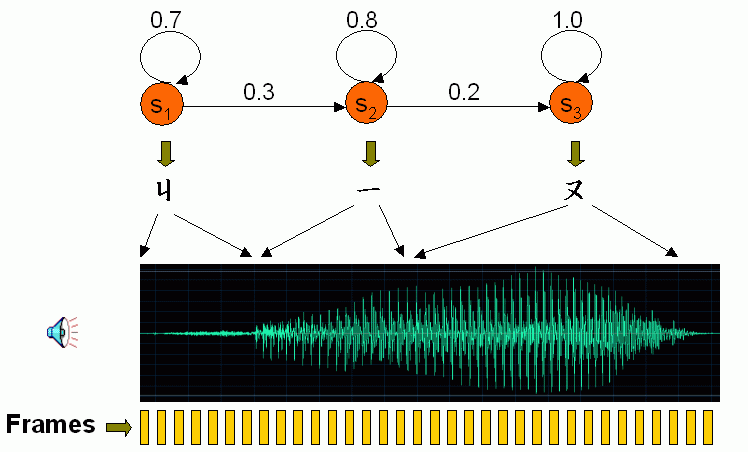
Before using DHMM, each frame is converted into a feature vector (such as MFCC), and each vector is transformed into a symbol. More specifically, all feature vectors are partitioned into clusters using vector quantization. We then use the index of a cluster to which a frame belongs to represent the symbol of that frame. That is, if the feature vector of frame i belongs to cluster k, then the symbol of frame i is k, as shown in the following expression:

k = O(i). In order to simplify the discussion, we define some variables shown next.

• frameNum: The number of frames for a given utterance
• dim: The dimension of the acoustic features used in our recognizer. (For instance, the basic MFCC has 12 dimensions.)
• stateNum: the number of states in a DHMM
• symbolNum: The number of symbols, or equivalently, the number of clusters after vector quantization.

Usually we use the state and transition probabilities to characterize a given DHMM, as follows.

• We use a stateNum×stateNum matrix A to denote the transition probability, in which A(i, j) denotes the probability from state i to j. For instance, the probability of transition from state 1 to 2 is 0.3, hence A(1, 2) = 0.3. In general, A(i, j) satisfies the following conditions:
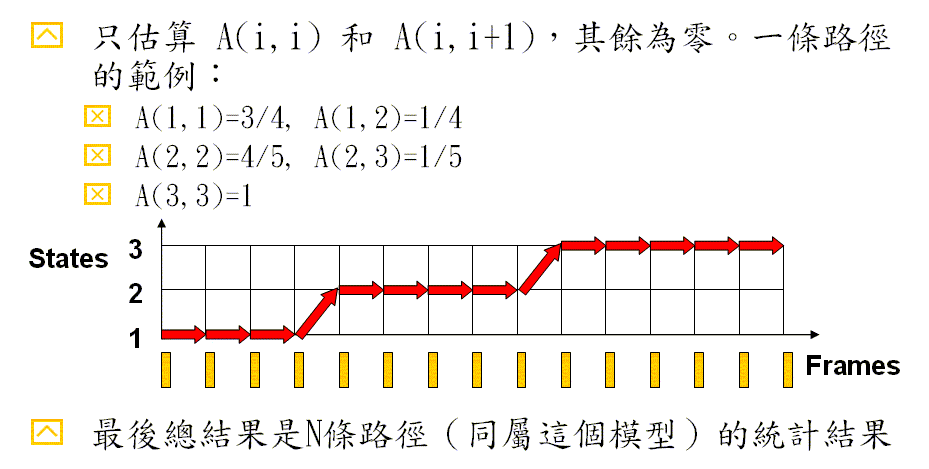
  • State transitions are allowed only between neighboring states. Hence A(i, j) = 0 if j≠i and j≠i+1。
  • For a given state, the self-state and next-state transition probabilities should sum to 1. Namely, A(i, i) + A(i, i+1) = 1, for all i.
• We use a symbolNum×stateNum matrix B to denote the state probability, in which B(k, j) denotes the probability to which symbol k belongs to state j. Therefore to compute the probability of frame i being generated by state j, we need to find the corresponding symbol k=O(i), and then retrieve the probability from B(k, j).

Assume that we already have matrices A and B for the DHMM of 「九」. Then for a given utterance, we can use Viterbi decoding to evaluate the probability of the utterance being generated by the DHMM. Viterbi decoding is based on the concept of dynamic program to assign each frame to a state such the accumulated probability can be maximized, as follows.

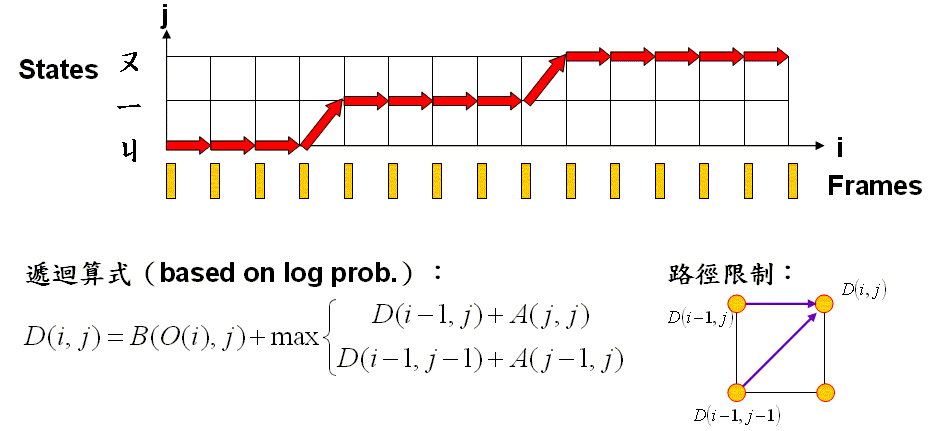
1. The optimum-value function D(i, j) is defined as the maximum probability between t(1:i) and r(1:j), where t(1:i) the feature vectors of frame 1 to i, r(1:j) is the DHMM formed by state 1 to j. The optimum mapping path from (1, 1) to (i, j) is sought to minimize D(i, j).
2. The recursion of D(i, j) can be expressed as follows: D(i, j) = B(O(i), j) + max{D(i-1, j)+A(j, j), D(i-1, j-1)+A(j-1, j)}. The boundary conditions is D(1, j) = p(1, j) + B(O(1), j), j = 1 ~ stateNum, where p(1, j) denotes the initial state probability for state j.
3. The final answer is D(m, n).

The schematic diagram is shown next: Note that in the above expression, we are using log probabilities for the following reasons:

• Reduce the round-off errors due to repeated multiplications.
• Use addition instead of multiplication to reduce computation load.

Based on Viterbi decoding, we can find the optimum assignment of frames to states as well as the accumulated log probability of a given utterance to a DHMM. A larger log probability indicates the utterance is likely to be the voice command of the corresponding DHMM.

To evaluate the probability of frame i to state j, there are two different methods:

• For DHMM, we need to find the corresponding symbol O(i) and then look up the value of B(O(i), j) from matrix B.
• For CHMM, B(O(i),j) is defined by a continuous probability density function. Please refer to the next section for detail.

For a given DHMM, how can we obtain the optimum values of matrices A and B? Via the concept of MLE, we know that the optimum values of of A and B should generate the maximum total log probability of all training utterance. As a result, we can search the values for A and B for generating the maximum total log probability.

The procedure to find the optimum values of A and B is called re-estimation. The basic concept is close to that of k-means (Forgy's method) which identify parameters by Picard iteration. That is, we can guess the values of A and B first, then perform Viterbi decoding, and then identify A and B again based on the given optimum path, until the values of A and B converge. We can prove that during the iterations, the total probability will increase monotonically. However, we cannot guarantee the identify values of A and B is the global optimum values. The steps of re-estimation are explained next.

1. Convert all utterances into acoustic features, say, 39-dimensional MFCC.
2. Perform vector quantization on all feature vectors and find the symbol (index of a cluster center) of each feature vector.
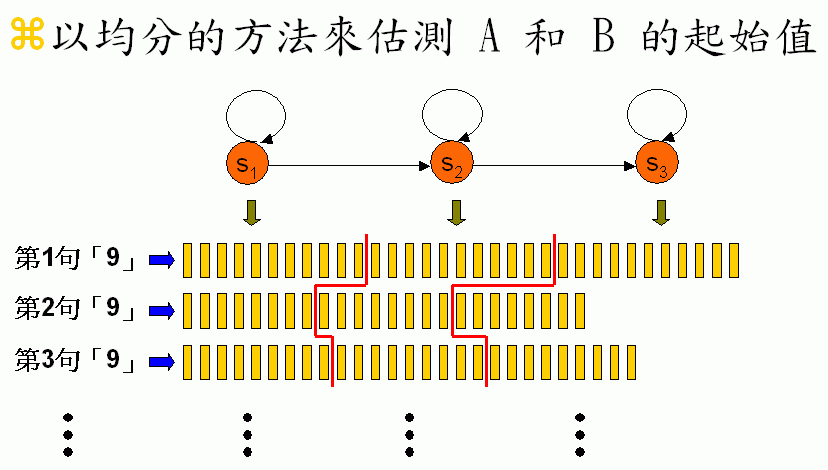
3. Guess the initial values of A and B. If there is no manual transcription, we can adopt the simple strategy of "equal division" shown next.
4. Iterate the following steps until the values of A and B converge.
   • Viterbi decoding: Given A and B of an DHMM, find the optimum mapping paths of all the corresponding utterances of this DHMM.
   • Re-estimation: Use the optimum mapping paths to estimate the values of A and B.

An example of estimating A is shown next: An example of estimating B is shown next: If we use C(i,j) to denote the probability to which frame i belongs to state j, then C(i,j) = B(O(i),j). Base on the path in the previous example, we can obtain the following values for C(i, j):

• State 1: C(1,1)=B(2,1)=1/4, C(2,1)=B(1,1)=1/4, C(3,1)=B(3,1)=2/4, C(4,1)=B(3,1)=2/4
• State 2: C(5,2)=B(1,1)=3/5, C(6,2)=B(1,1)=3/5, C(7,2)=B(2,1)=2/5, C(8,2)=B(1,1)=3/5, C(9,2)=B(2,1)=2/5
• State 2: C(10,3)=B(4,3)=4/6, C(11,3)=B(4,3)=4/6, C(12,3)=B(4,3)=4/6, C(13,3)=B(2,3)=2/6, C(14,3)=B(2,3)=2/6, C(15,3)=B(4,3)=4/6

If we use P(A, B, Path) as our objective function, then the above re-estimation can guarantee the monotonic increasing of the objective function, based on the following two facts.

1. When A and B is given, Viterbi decoding can find the optimum mapping path to maximize P(A, B, Path).
2. When the mapping path (Path) is given, re-estimation can find the optimum A and B to maximize P(A, B, Path).

The first fact is obvious since the goal of Viterbi Decoding is to maximize the probability of each path, hence their total P(A, B, Path) will also be maximized. The second fact is also obvious, to be explained next.

Take the above example for instance, the probability of the given path can be decomposed into three components based on each state:

• State 1: C(1,1)A(1,1)C(2,1)A(1,1)C(3,1)A(1,1)C(4,1)A(1,2) = A(1,1)³A(1,2)C(1,1)C(2,1)C(3,1)C(4,1)
• State 2: C(5,2)A(2,2)C(6,2)A(2,2)C(7,2)A(2,2)C(8,2)A(2,2)C(9,2)A(2,3) = A(2,2)⁴A(2,3)C(5,2)C(6,2)C(7,2)C(8,2)C(9,2)
• State 3: C(10,3)A(3,3)C(11,3)A(3,3)C(12,3)A(3,3)C(13,3)A(3,3)C(14,3)A(3,3)C(15,3) = A(3,3)⁵C(10,3)C(11,3)C(12,3)C(13,3)C(14,3)C(15,3)

Since we have N paths for N utterances, the total probability is the product of these N paths. When we are identifying the optimum values of A and B, we need to take these N paths into consideration. We shall decompose the total probability over N path into the probability associated with each state for finding the optimum values of A and B, as follows.

First of all, we shall derive the optimum value of matrix A. For any given state, we can define the following quantities:

• a: self-transition count (known)
• b: next-transition count (known)
• p: self-transition prob. (unknown)
• q: next-transition prob. (unknown)

Since we want to optimize the total transition probability associated with this state, we can form the following optimization problem: Max J(p, q) = p^a q^b s.t. p≧0, q≧, and p + q = 1 We need to apply the theorem that the arithmetic mean is greater than or equal to the geometric mean: x₁ + x₂ + ... + x_n ≧ n (x₁ x₂ ... x_n)^1/n The equality holds only when x₁ = x₂ = ... = x_n. Based on the above inequality, we have p/a + p/a + ... + q/b + q/b ... ≧ (a + b) [(p/a)^a(q/b)^b]^1/(a+b) 1 ≧ (a + b) [(p/a)^a(q/b)^b]^1/(a+b) The maximum value of J(p, q) = p^a q^b is a^ab^b/(a+b)^a+b, which happens at p/a = q/b, or equivalently, p=a/(a+b), q=b/(a+b).

Secondly, we shall derive the optimum value of B. For any given state, assume that frames of this state belong to 3 clusters. We can define the following quantities:

• Symbol count: a, b, c (known)
• State prob: p, q, r (unknown)

Since we want to optimize the total state probability associated with this state, we can form the following optimization problem: J(p, q, r) = p^a q^b r^c where p, q, r must satisfy p + q + r = 1. Based on the theorem (the arithmetic mean is greater than or equal to the geometric mean), we can obtain the optimum parameters p=a/(a+b+c), q=b/(a+b+c) , r=c/(a+b+c).

Therefore by decomposing the total probability of N paths into the probability associated with each state, we can identify the optimum values of the transition and state probabilities of this state. This completes the coverage of re-estimation which can guarantee the monotonic non-decreasing of the total log probability.

---

Data Clustering and Pattern Recognition (資料分群與樣式辨認)