為方便說明,我們假設我們的目標示要建立一個 0 ~ 9 的數字語音辨識系統,建立流程可以分成兩大步驟:
- 收集語料:由於我們的目標是語者無關的語音辨識,所以我們所收集的語料要盡量涵蓋各種可能的變化,例如:
- 錄音的人:各種不同的人,包含男女老少、高矮胖瘦等,以及各種南腔北調。
- 錄音裝置:取用不同的裝置,例如不同的麥克風、不同的音效卡等。
- 周遭環境:除了要在安靜的辦公室進行錄音外,也可以在吵雜的環境錄音,以增強語音辨識系統對於雜訊的抵抗力。
- 辨識系統的設計和測試:這也是我們下面的重點。
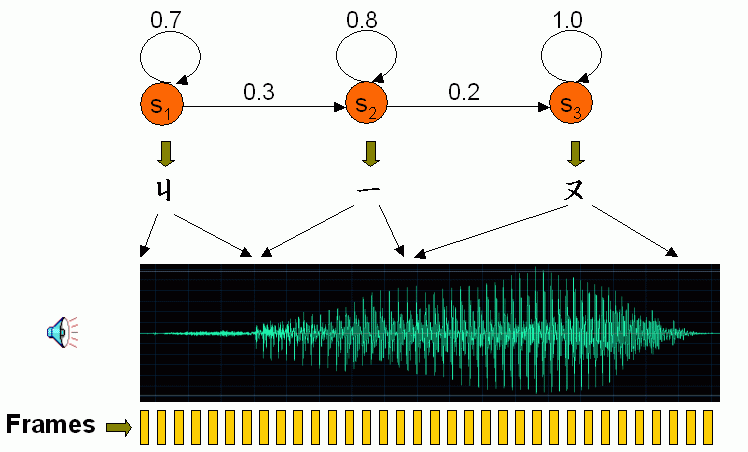
由於每一個音框都會轉成一個語音特徵向量,我們首先使用 VQ 來將這些特徵向量轉成符號(Symbols),換句話說,每一個音框所對應的 VQ 群聚的索引值(Index),即是此音框的符號。若以數學來表示,k = O(i) 即代表 frame i 被分到 cluster k。
為了簡化討論,首先我們定義一些常用的數量:
- frameNum:一段語音所切出的音框個數。
- dim:每一個音框所對應的語音特徵向量的維度(例如基本的 MFCC 有 12 維)。
- stateNum:一個 DHMM 的狀態個數
- symbolNum:符號的個數,也就是 VQ 後的群數
HMM 的參數,就是指「狀態機率」和「轉移機率」,說明如下:
- 我們通常以矩陣 A 來表示轉移機率,其維度是 stateNum x stateNum,其中 A(i, j) 即是指由狀態 i 跳到狀態 j 的機率值。例如在上圖中,由狀態 1 跳到狀態 2 的機率是 0.3,因此 A(1, 2) = 0.3。一般而言,A(i, j) 滿足下列條件:
- 在進行次轉移時,我們只允許搜尋路徑跳到下一個相鄰的狀態,因此 A(i, j) = 0 if j≠i and j≠i+1。
- 對於某一個狀態而言,所有的轉移機率總和為 1,因此 A(i, i) + A(i, i+1) = 1。
- 我們通常以矩陣 B 來表示狀態機率,其維度是 symbolNum x stateNum,B(k,j) 即是指符號 k 隸屬於狀態 j 的機率值。換句話說,B 定義了由「符號」到「狀態」的機率,因此給定第 i 個音框,我們必須先由 O(i) 找出這個音框所對應的符號 k,然後再由 B(k,j) 找出此音框屬於狀態 j 的機率。
- 目標函數:定義 D(i, j) 是 t(1:i) 和 r(1:j) 之間的最大的機率,t(1:i) 是前 i 個音框的特徵向量所成的矩陣,r(1:j) 則是由前 j 個狀態所形成的 DHMM,對應的最佳路徑是由 (1, 1) 走到 (i, j)。
- 遞迴關係:D(i, j) = B(O(i), j) + max{D(i-1, j)+A(j, j), D(i-1, j-1)+A(j-1, j)}
- 端點條件:D(1, j) = p(1, j) + B(O(1), j), j = 1 ~ stateNum
- 最後答案:D(m, n)
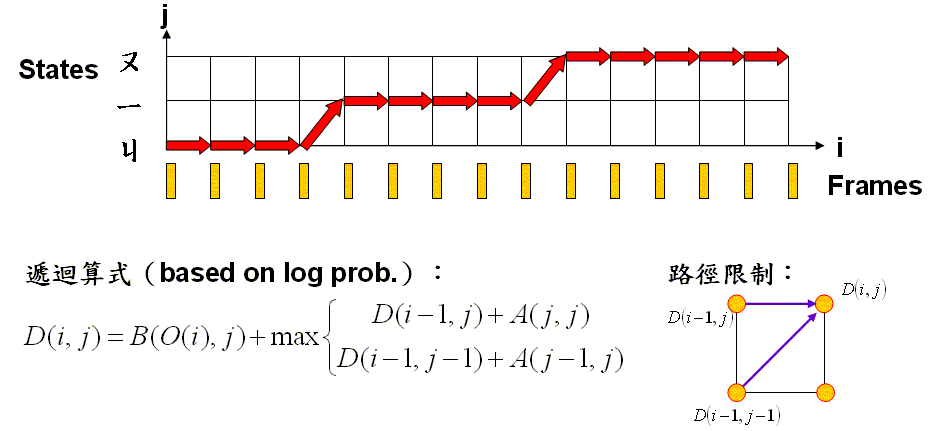
- 以加法來取代乘法,降低計算的複雜度。
- 避開了由於連乘所造成的數值誤差。
有關於 B(O(i),j)的定義,都是「音框 i 隸屬於狀態 j 的機率」,但是在 DHMM 和 CHMM 的算法差異很大,說明如下:
- 在 DHMM,若要計算 B(O(i),j),我們必須先找到音框 i 所對應的符號 O(i),然後在經由查表法查到此符號 O(i) 屬於狀態 j 的機率是 B(O(i), j)。
- 在 CHMM,B(O(i),j) 是由一個連續的機率密度函數所定義,請見下一小節說明。
但是,如何經由大量語料來估測每個 HMM 模型的最佳參數值 A 和 B 呢?首先,我們必須先定義什麼是「最佳參數」:對某一個特定模型而言,最佳參數值 A 和 B 應能使語料產生最大的對數機率總和。這個定義和 MLE 完全相同,也非常合理。
計算最佳參數的方法,稱為 Re-estimation,其原理非常類似 batch k-means (Forgy's method) 的方法,先猜 A 和 B 的值,再反覆進行 Viterbi Decoding,然後再重新估算 A 和 B 的值,如此反覆計算,我們可以證明在疊代過程中,機率總和會一路遞增,直到逼近最佳值。(但是,就如同 k-means Clustering,我們並無法證明所得到的機率值是 Global Maximum,因此在訓練的過程中,可以使用不同的啟始參數,看看是否在反覆疊代後,能夠得到更好的機率總和。)求取參數的方法說明如下:
- 將所有的訓練語句切出音框,並將每一個音框轉成語音特徵向量,例如 39 維的 MFCC。
- 對所有語音特徵向量進行VQ,找出每一個向量所對應的 symbol(此即為對應的中心點或codeword)
- 先猜一組 A 和 B 的啟始值。如果沒有人工的標示資料,我們可以使用簡單的「均分法」,示意圖如下:
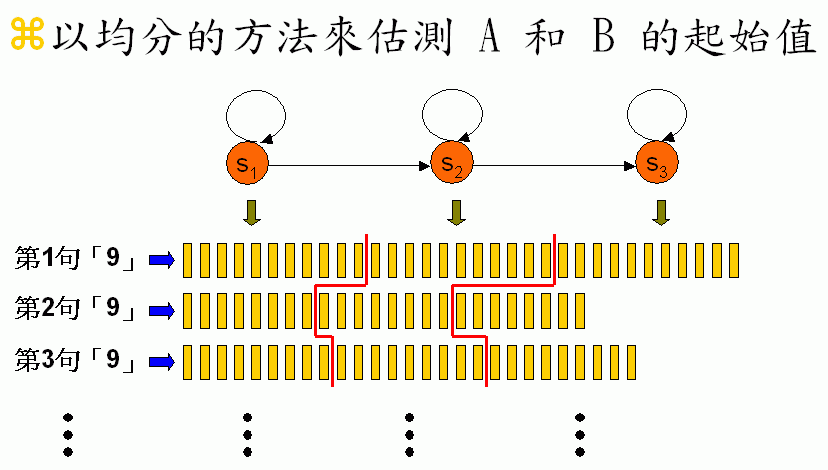
- 反覆進行下列兩步驟,直到收斂
- Viterbi decoding:在 A 和 B 固定的情況下,利用 Viterbi decoding,找出 n 句「九」的語料所對應的 n 條最佳路徑。
- Re-estimation:利用這 n 條最佳路徑,重新估算 A 和 B。
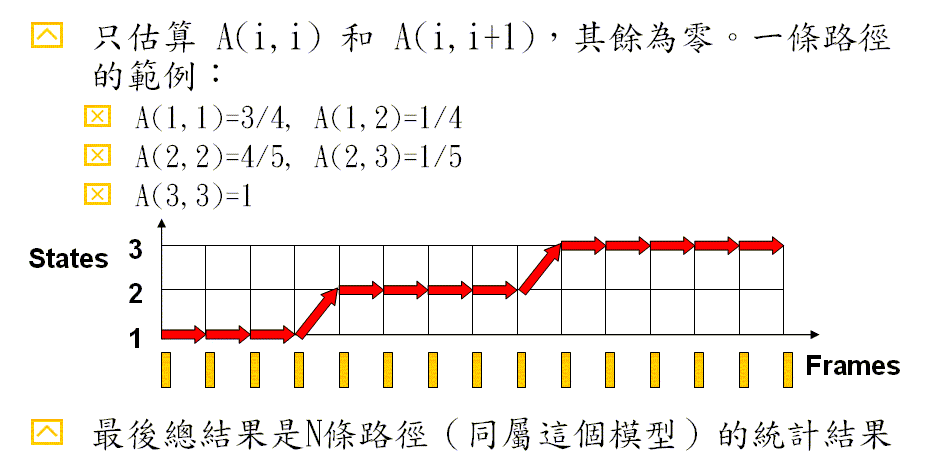

- State 1: D(1,1)=B(2,1)=1/4, D(2,1)=B(1,1)=1/4, D(3,1)=B(3,1)=2/4, D(4,1)=B(3,1)=2/4
- State 2: D(5,2)=B(1,1)=3/5, D(6,2)=B(1,1)=3/5, D(7,2)=B(2,1)=2/5, D(8,2)=B(1,1)=3/5, D(9,2)=B(2,1)=2/5
- State 2: D(10,3)=B(4,3)=4/6, D(11,3)=B(4,3)=4/6, D(12,3)=B(4,3)=4/6, D(13,3)=B(2,3)=2/6, D(14,3)=B(2,3)=2/6, D(15,3)=B(4,3)=4/6
假設我們的目標函數可以寫成 P(A, B, Path),則上述求參數的方法會讓 P(A, B, Path)逐次遞增,直到收斂,因為:
- 在 A, B 固定時,Viterbi decoding 會找出最佳的路徑,使 P(A, B, Path) 有最大值
- 在路徑(Path)固定時,Re-estimation 會找出最佳的 A, B 值以使 P(A, B, Path)有最大值
以上述範例而言,此條路徑的總機率可以拆解成在三個 state 中的機率:
- State 1: D(1,1)A(1,1)D(2,1)A(1,1)D(3,1)A(1,1)D(4,1)A(1,2) = A(1,1)3A(1,2)D(1,1)D(2,1)D(3,1)D(4,1)
- State 2: D(5,2)A(2,2)D(6,2)A(2,2)D(7,2)A(2,2)D(8,2)A(2,2)D(9,2)A(2,3) = A(2,2)4A(2,3)D(5,2)D(6,2)D(7,2)D(8,2)D(9,2)
- State 3: D(10,3)A(3,3)D(11,3)A(3,3)D(12,3)A(3,3)D(13,3)A(3,3)D(14,3)A(3,3)D(15,3)A(3,3) = A(3,3)6D(10,3)D(11,3)D(12,3)D(13,3)D(14,3)D(15,3)
以下將求取 A 和 B 的最佳值。對任一個 state 而言,假設共有 a+b 個音框屬於這個 state,其中
- p: self-transition prob.(未知)
- q: next-transition prob.(未知)
- a: self-transition count(已知)
- b: next-transition count(已知)
對任一個 state 而言,假設這個 state 內的音框只屬於三個 cluster,機率分別是 p, q, r:
- State prob: p, q, r(未知)
- Symbol count: a, b, c(已知)
本章節說明,請參考下列投影片:
Data Clustering and Pattern Recognition (資料分群與樣式辨認)
