MATLAB Function Reference

ode45, ode23, ode113, ode15s, ode23s, ode23t, ode23tb

解常微分等式(ODEs，ordinary differential equations)的初始值問題

Syntax

[T,Y] = solver(odefun,tspan,y0)
[T,Y] = solver(odefun,tspan,y0,options)
[T,Y] = solver(odefun,tspan,y0,options,p1,p2...)
[T,Y,TE,YE,IE] = solver(odefun,tspan,y0,options)

其中 solver 是 ode45、ode23、ode113、ode15s、ode23s、ode23t 或 ode23tb 的其中一個。

Arguments

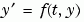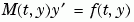odefun	求微分等式右邊函數值的函數。所有的解題器(solver)都以 的模式解題，當問題牽涉到矩陣時，以 的模式解題。ode23s 解題器只可以解包含常數矩陣的等式。ode15s 和 ode23t 可以解包含 singular 矩陣的問題，例如，differential-algebraic equations (DAEs)。
tspan	定義積分範圍的向量，[t0 tf]。要在特定時間得到答案(全部增加或全部減少)，可以使用 tspan = [t0,t1,...,tf]。
y0	初始狀態的向量。
options	由 odeset 函數產生的選擇性積分參數。詳細情形請看 odeset。
p1,p2...	傳到 odefun 的選擇性參數。

Description

[T,Y] = solver(odefun,tspan,y0) 而 tspan = [t0 tf] 求微分等式 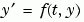系統的積分，時間從 t0 到 tf，初始值是 y0。函數 f = odefun(t,y)，對一個純量 t 和一個直行向量 y，必須回傳一個對應 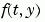的直行向量f。解答陣列 Y 的每個橫列對應到一個回傳的時間直行向量 T。使用 tspan = [t0,t1,...,tf]，可以在特定時間 t0,t1,...,tf 得到答案，(全部增加或全部減少)。

[T,Y] = solver(odefun,tspan,y0,options) 與之前一樣的解題，預設參數以定義在 odeset 函數產生 options 的 property values 取代。一般使用的屬性包含一個純量的對應錯誤容忍值(relative error tolerance) RelTol (預設值是(1e-3)，還有一個絕對錯誤容忍值的向量 AbsTol (所有元素的預設值都是 1e-6)。詳細情形請看 odeset 。

[T,Y] = solver(odefun,tspan,y0,options,p1,p2...) 與之前一樣的解題，當它被呼叫時，傳入額外的參數 p1,p2... 到 odefun 函數。如果沒有設定 option，使用 options = []。

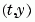[T,Y,TE,YE,IE] = solver(odefun,tspan,y0,options) 與之前一樣的解題，同時還尋找 ，事件函數(event function)，哪裡是零。對於每個事件函數(event function)，你可以定義零的時候積分是否停止，還有過零的方向是否有關係。這是經由設定 Events 屬性，@EVENTS，還有產生一個函數[value,isterminal,direction] = EVENTS(t,y)達成的。對第 i 個事件函數：

• value(i) 是函數值。
• isterminal(i) = 1 如果積分在這個事件函數零的時候要停止，否則則設成 0。
• direction(i) = 0 如果所有的零都要計算(預設)，+1 如果只計算事件函數遞減時的零，-1 如果只計算事件函數遞減時的零。

對應的輸入 TE、YE 和 IE 分別傳回事件發生時間，事件當時的解，和事件函數消失時的索引值 i。

如果你定義一個輸出函數 OutputFcn 屬性，解題器會在每個時間點後與算好的解一起呼叫它。提供四個輸出函數：odeplot、odephas2、odephas3、odeprint。當解題器被呼叫而沒有輸出參數，它會在計算時呼叫預設的 odeplot 來畫出解答。odephas2 和 odephas3 分別產生二維和三維的圖形。odeprint 在螢幕上顯示解答元素。預設的情形，所有解答的元素都會被傳到輸出函數。不過經由提供一個如同 OutputSel 屬性的索引值向量，你可以只傳特定的元素。例如，如果你呼叫解題器且沒有輸出元素，而把 OutputSel 的值設成 [1,3]，解題器會畫出解答元素的 1 和 3 當它們被計算時。

於嚴謹的解題器 ode15s、ode23s、ode23t 和 ode23tb，為了信賴度和效率，Jacobian matrix 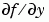是必需的。使用 odeset 來設 Jacobian 為 @FJAC 如果 FJAC(T,Y) 傳回 Jacobian 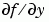，或是設為矩陣 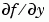如果 Jacobian 是常數。如果沒有設定 Jacobian 屬性(用預設值)， 是用有限的積分來逼近。如果 ODE 函數是程式寫好的，設定 Vectorized 屬性 'on'，如此 odefun(T,[Y1,Y2 ...]) 傳回 [odefun(T,Y1),odefun(T,Y2) ...]。如果 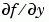是一個稀疏矩陣(sparse matrix)，設 JPattern 屬性為 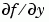的稀疏模式(sparsity pattern)，i.e.，一個稀疏矩陣 S 其中 S(i,j) = 1 如果 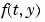的第 i 個元素由 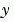第 j 個元素決定，否則就是0。

ODE 系列的解題器經由 time- 和 state-dependent 的矩陣 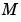可以解答 模式的問題。(ode23s 解題器只可以解常數矩陣的等式。)如果問題有一個矩陣，產生一個函數 M = MASS(t,y) 會傳回矩陣的值，使用 odeset 來設定 Mass 屬性為 @MASS。如果矩陣是常數，則矩陣可以用來當作 Mass 屬性的值。關於 state-dependent 矩陣的問題比較困難：

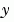• 如果矩陣不依賴狀態變數 且函數 MASS 被呼叫時只有一個輸入參數t，設定 MStateDependence 屬性為 'none'。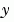
• 如果矩陣輕微的依賴 ，設定MStateDependence 為 'weak' (預設值)，否則設成 'strong'。在其他的情形下，MASS 函數被呼叫時需有兩個參數(t,y)。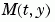

如果有許多微分等式，利用稀疏矩陣是很重要的：

• 傳回一個稀疏矩陣 。
• 使用 JPattern 屬性提供 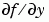的稀疏模式，或是使用 Jacobian 屬性提供稀疏矩陣 。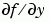
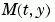• 對於強烈 state-dependent 的 ，設定 MvPattern 為稀疏矩陣 S 其中 S(i,j) = 1 如果對於任何 k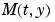， 的(i,k)元素依賴 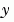的 j 元素，否則設為 0。

如果矩陣 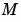是singular，則 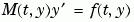是一個微分的代數問題。只有在 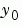前後一致時，DAEs 會有解。就是說，如果有一個向量 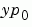其中

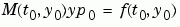。 ode15s 和 ode23t 解題器可以解索引值 1 的 DAEs 保證 y0 會足夠乎近前後一致。如果有一個矩陣，你可以用odeset 來設定MassSingular 屬性為 'yes'，'no'，或是 'maybe'。'maybe' 的預設值會讓解題器測是問題是否是 DAE。你可以提供 yp0 當作 InitialSlope 屬性的值。預設值是零向量。如果問題是 DAE，而 y0 和 yp0 不是一致的，解題器會把它們當作是猜測，試著計算與猜測值一致的值，然後繼續解題。當解 DAEs 時，將問題公式化是非常有益處的，如此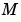， 是一個對角線矩陣(diagonal matrix)(a semi-explicit DAE)。

Solver	Problem Type	Order of Accuracy	When to Use
ode45	Nonstiff	Medium	大部分的時後。這應該是你第一個嘗試的解題器。
ode23	Nonstiff	Low	如果用粗糙的錯誤容忍或是解普通嚴厲的問題。
ode113	Nonstiff	Low to high	如果要求嚴厲的錯誤容忍或是解計算密集的 ODE 檔案。
ode15s	Stiff	Low to medium	如果 ode45 因為問題是嚴謹的而執行緩慢。
ode23s	Stiff	Low	如果用粗糙的錯誤容忍去解嚴謹的系統且矩陣是常數。
ode23t	Moderately Stiff	Low	如果問題只是普通嚴謹且你需要解答沒有數值的影響。
ode23tb	Stiff	Low	如果用粗糙的錯誤容忍來解嚴謹的系統。

ODE 解題器使用的演算法依準確度 [6] 和它們設計要解的系統(嚴謹或不嚴謹)不同而有所不同。詳細情形請看 Algorithms。

Options

不同的解題器在選擇列表接受不同的參數。 更多的資訊在 odeset 和 MATLAB 文件 Mathematical Analysis 中的"微分等式"一節 Improving ODE Solver Performance 。

Parameters	ode45	ode23	ode113	ode15s	ode23s	ode23t	ode23tb
RelTol, AbsTol, NormControl
OutputFcn, OutputSel, Refine, Stats
Events
MaxStep, InitialStep
Jacobian, JPattern, Vectorized	--	--	--
Mass MStateDependence MvPattern MassSingular	-- --	-- --	-- --		-- -- --		--
InitialSlope	--	--	--		--		--
MaxOrder, BDF	--	--	--		--	--	--

Examples

Example 1. 一個不嚴謹系統的範例，描述無外力硬式物體的運動。

為了模擬這個系統，建立包含等式的 rigid 函數

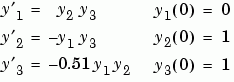
function dy = rigid(t,y)
dy = zeros(3,1);    % a column vector
dy(1) = y(2) * y(3);
dy(2) = -y(1) * y(3);
dy(3) = -0.51 * y(1) * y(2);

在這個範例中，我們用 odeset 命令改變錯誤容忍值，且在時間間隔 [0 12] 裡解題，在時間 0 時，初始狀態向量[0 1 1]。

options = odeset('RelTol',1e-4,'AbsTol',[1e-4 1e-4 1e-5]);
[T,Y] = ode45(@rigid,[0 12],[0 1 1],options);

畫出回傳陣列 Y 的直行對 T 的圖顯示解答

plot(T,Y(:,1),'-',T,Y(:,2),'-.',T,Y(:,3),'.')

Example 2. 一個嚴謹系統的範例，鬆弛震盪的 van der Pol 等式。週期的界限有部份的元素改變緩慢而這部份的問題相當嚴謹，交替著非常急劇的改變而這部份較不嚴謹。

為了模擬這個系統，建立包含等式的 vdp1000 函數

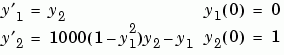
function dy = vdp1000(t,y)
dy = zeros(2,1);    % a column vector
dy(1) = y(2);
dy(2) = 1000*(1 - y(1)^2)*y(2) - y(1);

對於這個問題，我們將會用預設的相對和絕對容忍值(分別是 1e-3 和 1e-6)，在時間間隔 [0 3000] 裡解題，在時間 0 時，初始狀況向量 [2 0]。

[T,Y] = ode15s(@vdp1000,[0 3000],[2 0]);

畫出回傳矩陣 Y 的第一個直行對 T 的圖顯示解答

plot(T,Y(:,1),'-o'):

Algorithms

ode45 是以 explicit Runge-Kutta (4,5) 公式為基礎，Dormand-Prince pair。這是一個 一步(one-step) 解題器 - 在計算 y(tn)，它只需要前一個時間點的解答，y(tn-1)。一般來說，對於大多數問題 ode45 是當作"第一次嘗試"的最好函數。[3]

ode23 是 explicit Runge-Kutta (2,3) pair of Bogacki and Shampine 的建構。在粗糙的容忍值和適度的嚴謹度時，它可能比 ode45 更有效率。像 ode45，ode23 是一個一步(one-step)解題器。[2]

ode113 是一個 variable order Adams-Bashforth-Moulton PECE 解題器。在嚴厲的容忍值和當 ODE 檔案函數求取不易時，它可能比 ode45 更有效率。ode113 是一個 多步(multistep) 解題器 - 它通常需要多個之前時間點的解答來計算目前的答案。[7]

以上的演算法都是試圖解不嚴謹的系統。如果它們執行起來來過慢，試著使用以下其中一個嚴謹的解題器。

ode15s 是一個以numerical differentiation formulas(NDFs)為基礎的可變維度解題器。它選擇性地使用較無效率的 backward differentiation formulas (BDFs, 又稱為 Gear's method)。像 ode113，ode15s 是一個多步(multistep)解題器。嘗試 ode15s，當 ode45 失敗、或是非常沒有效率，而且你懷疑問題是嚴謹的時候，或是當解一個微分代數問題時。[9]，[10]

ode23s 是以 modified Rosenbrock formula of order 2 為基礎。因為它是一個一步(one-step)解題器，在粗糙的容忍值時，它可能比 ode15s 更有效率。它可以解一些用 ode15s 計算沒有效率的嚴謹問題。[9]

ode23t 是用 trapezoidal rule using a "free" interpolant 建構的。用這個解題器 如果問題只是普通嚴謹且你需要一個沒有數值影響的解答。ode23t 可以解 DAEs。[10]

ode23tb 是用 TR-BDF2 建構的，implicit Runge-Kutta formula with a first stage that is a trapezoidal rule step and a second stage that is a backward differentiation formula of order two。在結構上來說，同樣的重複矩陣被用來計算兩個階段。像 ode23s，在粗糙的容忍度時，這個解題器可能比 ode15s 更有效率。[8], [1]

See Also

@ (function_handle), odeset, odeget

References

[1]  Bank, R. E., W. C. Coughran, Jr., W. Fichtner, E. Grosse, D. Rose, and R. Smith, "Transient Simulation of Silicon Devices and Circuits," IEEE Trans. CAD, 4 (1985), pp 436-451.

[2]  Bogacki, P. and L. F. Shampine, "A 3(2) pair of Runge-Kutta formulas," Appl. Math. Letters, Vol. 2, 1989, pp 1-9.

[3]  Dormand, J. R. and P. J. Prince, "A family of embedded Runge-Kutta formulae," J. Comp. Appl. Math., Vol. 6, 1980, pp 19-26.

[4]  Forsythe, G. , M. Malcolm, and C. Moler, Computer Methods for Mathematical Computations, Prentice-Hall, New Jersey, 1977.

[5]  Kahaner, D. , C. Moler, and S. Nash, Numerical Methods and Software, Prentice-Hall, New Jersey, 1989.

[6]  Shampine, L. F. , Numerical Solution of Ordinary Differential Equations, Chapman & Hall, New York, 1994.

[7]  Shampine, L. F. and M. K. Gordon, Computer Solution of Ordinary Differential Equations: the Initial Value Problem, W. H. Freeman, San Francisco, 1975.

[8]  Shampine, L. F. and M. E. Hosea, "Analysis and Implementation of TR-BDF2," Applied Numerical Mathematics 20, 1996.

[9]  Shampine, L. F. and M. W. Reichelt, "The MATLAB ODE Suite," SIAM Journal on Scientific Computing, Vol. 18, 1997, pp 1-22.

[10]  Shampine, L. F., M. W. Reichelt, and J.A. Kierzenka, "Solving Index-1 DAEs in MATLAB and Simulink," SIAM Review, Vol. 41, 1999, pp 538-552.

nzmax

odefile