

| MATLAB Function Reference |   |
Solve initial value problems for ordinary differential equations (ODEs)
Syntax
[T,Y] = solver(odefun,tspan,y0) [T,Y] = solver(odefun,tspan,y0,options) [T,Y] = solver(odefun,tspan,y0,options,p1,p2...) [T,Y,TE,YE,IE] = solver(odefun,tspan,y0,options)
where solver is one of ode45, ode23, ode113, ode15s, ode23s, ode23t, or ode23tb.
Arguments
|
A function that evaluates the right-hand side of the differential equations. All solvers solve systems of equations in the form 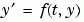 or problems that involve a mass matrix, or problems that involve a mass matrix, 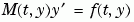 . The . The ode23s solver can solve only equations with constant mass matrices. ode15s and ode23t can solve problems with a mass matrix that is singular, i.e., differential-algebraic equations (DAEs). |
tspan |
A vector specifying the interval of integration, [t0 tf]. To obtain solutions at specific times (all increasing or all decreasing), use tspan = [t0,t1,...,tf]. |
y0 |
A vector of initial conditions. |
|
Optional integration argument created using the odeset function. See odeset for details. |
p1,p2... |
Optional parameters to be passed to odefun. |
Description
[T,Y] = with solver(odefun,tspan,y0)
tspan = [t0 tf] integrates the system of differential equations 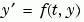 from time
from time t0 to tf with initial conditions y0. Function f = odefun(t,y), for a scalar t and a column vector y, must return a column vector f corresponding to 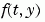 . Each row in solution array
. Each row in solution array Y corresponds to a time returned in column vector T. To obtain solutions at the specific times t0, t1,...,tf (all increasing or all decreasing), use tspan = [t0,t1,...,tf].
[T,Y] = solves as above with default integration parameters replaced by property values specified in solver(odefun,tspan,y0,options)
options, an argument created with the odeset function. Commonly used properties include a scalar relative error tolerance RelTol (1e-3 by default) and a vector of absolute error tolerances AbsTol (all components are 1e-6 by default). See odeset for details.
[T,Y] = solves as above, passing the additional parameters solver(odefun,tspan,y0,options,p1,p2...)
p1,p2... to the function odefun, whenever it is called. Use options = [] as a place holder if no options are set.
[T,Y,TE,YE,IE] = solves as above while also finding where functions of solver(odefun,tspan,y0,options)
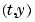 , called event functions, are zero. For each event function, you specify whether the integration is to terminate at a zero and whether the direction of the zero crossing matters. This is done by setting the
, called event functions, are zero. For each event function, you specify whether the integration is to terminate at a zero and whether the direction of the zero crossing matters. This is done by setting the Events property to, say, @EVENTS, and creating a function [value,isterminal,direction] = EVENTS(t,y). For the ith event function:
value(i) is the value of the function.isterminal(i) = 1 if the integration is to terminate at a zero of this event function and 0 otherwise. direction(i) = 0 if all zeros are to be computed (the default), +1 if only the zeros where the event function increases, and -1 if only the zeros where the event function decreases. Corresponding entries in TE, YE, and IE return, respectively, the time at which an event occurs, the solution at the time of the event, and the index i of the event function that vanishes.
If you specify an output function as the value of the OutputFcn property, the solver will call it with the computed solution after each time step. Four output functions are provided: odeplot, odephas2, odephas3, odeprint. When the solver is called with no output arguments, it calls the default odeplot to plot the solution as it is computed. odephas2 and odephas3 produce two- and three-dimnesional phase plane plots, respectively. odeprint displays the solution components on the screen. By default, all components of the solution are passed to the output function, but you can pass only specific components by providing a vector of indices as the value of the OutputSel property. For example, if you call the solver with no output arguments and set the value of OutputSel to [1,3], the solver plots solution components 1 and 3 as they are computed.
For the stiff solvers ode15s, ode23s, ode23t, and ode23tb, the Jacobian matrix 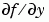 is critical to reliability and efficiency. Use
is critical to reliability and efficiency. Use odeset to set Jacobian to @FJAC if FJAC(T,Y) returns the Jacobian 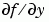 or to the matrix
or to the matrix 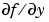 if the Jacobian is constant. If the
if the Jacobian is constant. If the Jacobian property is not set (the default),  is approximated by finite differences. Set the
is approximated by finite differences. Set the Vectorized property 'on' if the ODE function is coded so that odefun(T,[Y1,Y2 ...]) returns [odefun(T,Y1),odefun(T,Y2) ...]. If 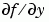 is a sparse matrix, set the
is a sparse matrix, set the JPattern property to the sparsity pattern of 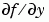 , i.e., a sparse matrix
, i.e., a sparse matrix S with S(i,j) = 1 if the ith component of 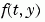 depends on the
depends on the jth component of 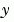 , and 0 otherwise.
, and 0 otherwise.
The solvers of the ODE suite can solve problems of the form  , with time- and state-dependent mass matrix
, with time- and state-dependent mass matrix 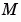 . (The
. (The ode23s solver can solve only equations with constant mass matrices.) If a problem has a mass matrix, create a function M = MASS(t,y) that returns the value of the mass matrix, and use odeset to set the Mass property to @MASS. If the mass matrix is constant, the matrix should be used as the value of the Mass property. Problems with state-dependent mass matrices are more difficult:
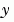 and the function
and the function MASS is to be called with one input argument, t, set the MStateDependence property to 'none'. 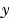 , set
, set MStateDependence to 'weak' (the default) and otherwise, to 'strong'. In either case, the function MASS is called with the two arguments (t,y). If there are many differential equations, it is important to exploit sparsity:
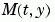 .
. 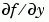 using the
using the JPattern property or a sparse 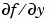 using the
using the Jacobian property. 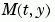 , set
, set MvPattern to a sparse matrix S with S(i,j) = 1 if for any k, the (i,k) component of 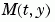 depends on component
depends on component j of 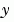 , and
, and 0 otherwise. If the mass matrix 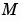 is singular, then
is singular, then 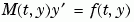 is a differential algebraic equation. DAEs have solutions only when
is a differential algebraic equation. DAEs have solutions only when 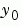 is consistent, that is, if there is a vector
is consistent, that is, if there is a vector 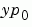 such that
such that
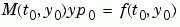 . The
. The ode15s and ode23t solvers can solve DAEs of index 1 provided that y0 is sufficiently close to being consistent. If there is a mass matrix, you can use odeset to set the MassSingular property to 'yes', 'no', or 'maybe'. The default value of 'maybe' causes the solver to test whether the problem is a DAE. You can provide yp0 as the value of the InitialSlope property. The default is the zero vector. If a problem is a DAE, and y0 and yp0 are not consistent, the solver treats them as guesses, attempts to compute consistent values that are close to the guesses, and continues to solve the problem. When solving DAEs, it is very advantageous to formulate the problem so that 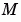 is a diagonal matrix (a semi-explicit DAE).
is a diagonal matrix (a semi-explicit DAE).
The algorithms used in the ODE solvers vary according to order of accuracy [6] and the type of systems (stiff or nonstiff) they are designed to solve. See Algorithms for more details.
Options
Different solvers accept different parameters in the options list. For more information, see odeset and Improving ODE Solver Performance in the "Differential Equations" section of the Mathematical Analysis MATLAB documentation.
Examples
Example 1. An example of a nonstiff system is the system of equations describing the motion of a rigid body without external forces.
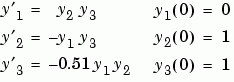
To simulate this system, create a function rigid containing the equations
function dy = rigid(t,y) dy = zeros(3,1); % a column vector dy(1) = y(2) * y(3); dy(2) = -y(1) * y(3); dy(3) = -0.51 * y(1) * y(2);
In this example we change the error tolerances using the odeset command and solve on a time interval of [0 12] with an initial condition vector [0 1 1] at time 0.
options = odeset('RelTol',1e-4,'AbsTol',[1e-4 1e-4 1e-5]);
[T,Y] = ode45(@rigid,[0 12],[0 1 1],options);
Plotting the columns of the returned array Y versus T shows the solution
plot(T,Y(:,1),'-',T,Y(:,2),'-.',T,Y(:,3),'.')
Example 2. An example of a stiff system is provided by the van der Pol equations in relaxation oscillation. The limit cycle has portions where the solution components change slowly and the problem is quite stiff, alternating with regions of very sharp change where it is not stiff.
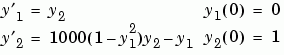
To simulate this system, create a function vdp1000 containing the equations
function dy = vdp1000(t,y) dy = zeros(2,1); % a column vector dy(1) = y(2); dy(2) = 1000*(1 - y(1)^2)*y(2) - y(1);
For this problem, we will use the default relative and absolute tolerances (1e-3 and 1e-6, respectively) and solve on a time interval of [0 3000] with initial condition vector [2 0] at time 0.
[T,Y] = ode15s(@vdp1000,[0 3000],[2 0]);
Plotting the first column of the returned matrix Y versus T shows the solution
plot(T,Y(:,1),'-o'):
Algorithms
ode45 is based on an explicit Runge-Kutta (4,5) formula, the Dormand-Prince pair. It is a one-step solver - in computing y(tn), it needs only the solution at the immediately preceding time point, y(tn-1). In general, ode45 is the best function to apply as a "first try" for most problems. [3]
ode23 is an implementation of an explicit Runge-Kutta (2,3) pair of Bogacki and Shampine. It may be more efficient than ode45 at crude tolerances and in the presence of moderate stiffness. Like ode45, ode23 is a one-step solver. [2]
ode113 is a variable order Adams-Bashforth-Moulton PECE solver. It may be more efficient than ode45 at stringent tolerances and when the ODE file function is particularly expensive to evaluate. ode113 is a multistep solver - it normally needs the solutions at several preceding time points to compute the current solution. [7]
The above algorithms are intended to solve nonstiff systems. If they appear to be unduly slow, try using one of the stiff solvers below.
ode15s is a variable order solver based on the numerical differentiation formulas (NDFs). Optionally, it uses the backward differentiation formulas (BDFs, also known as Gear's method) that are usually less efficient. Like ode113, ode15s is a multistep solver. Try ode15s when ode45 fails, or is very inefficient, and you suspect that the problem is stiff, or when solving a differential-algebraic problem. [9], [10]
ode23s is based on a modified Rosenbrock formula of order 2. Because it is a one-step solver, it may be more efficient than ode15s at crude tolerances. It can solve some kinds of stiff problems for which ode15s is not effective. [9]
ode23t is an implementation of the trapezoidal rule using a "free" interpolant. Use this solver if the problem is only moderately stiff and you need a solution without numerical damping. ode23t can solve DAEs. [10]
ode23tb is an implementation of TR-BDF2, an implicit Runge-Kutta formula with a first stage that is a trapezoidal rule step and a second stage that is a backward differentiation formula of order two. By construction, the same iteration matrix is used in evaluating both stages. Like ode23s, this solver may be more efficient than ode15s at crude tolerances. [8], [1]
See Also
@ (function_handle), odeset, odeget
References
[1] Bank, R. E., W. C. Coughran, Jr., W. Fichtner, E. Grosse, D. Rose, and R. Smith, "Transient Simulation of Silicon Devices and Circuits," IEEE Trans. CAD, 4 (1985), pp 436-451.
[2] Bogacki, P. and L. F. Shampine, "A 3(2) pair of Runge-Kutta formulas," Appl. Math. Letters, Vol. 2, 1989, pp 1-9.
[3] Dormand, J. R. and P. J. Prince, "A family of embedded Runge-Kutta formulae," J. Comp. Appl. Math., Vol. 6, 1980, pp 19-26.
[4] Forsythe, G. , M. Malcolm, and C. Moler, Computer Methods for Mathematical Computations, Prentice-Hall, New Jersey, 1977.
[5] Kahaner, D. , C. Moler, and S. Nash, Numerical Methods and Software, Prentice-Hall, New Jersey, 1989.
[6] Shampine, L. F. , Numerical Solution of Ordinary Differential Equations, Chapman & Hall, New York, 1994.
[7] Shampine, L. F. and M. K. Gordon, Computer Solution of Ordinary Differential Equations: the Initial Value Problem, W. H. Freeman, San Francisco, 1975.
[8] Shampine, L. F. and M. E. Hosea, "Analysis and Implementation of TR-BDF2," Applied Numerical Mathematics 20, 1996.
[9] Shampine, L. F. and M. W. Reichelt, "The MATLAB ODE Suite," SIAM Journal on Scientific Computing, Vol. 18, 1997, pp 1-22.
[10] Shampine, L. F., M. W. Reichelt, and J.A. Kierzenka, "Solving Index-1 DAEs in MATLAB and Simulink," SIAM Review, Vol. 41, 1999, pp 538-552.
 | nzmax | odefile |  |