MATLAB Function Reference

griddata

資料分格(data gridding)

Syntax

ZI = griddata(x,y,z,XI,YI)
[XI,YI,ZI] = griddata(x,y,z,xi,yi)
[...] = griddata(...,method)

Description

ZI = griddata(x,y,z,XI,YI) 使(通常是)不一致的空間向量 (x,y,z) 中的資料對應到一個符合 z = f(x,y) 形式的表面上。griddata 用由 (XI,YI) 定義的點修改表面來產生 ZI。這個表面總是會經過資料點。XI 和 YI 通常形成均勻的格子。(如同 meshgrid 所產生的)。

XI 可以是一個橫列向量，在這個情形下，它定義一個直行元素是常數的矩陣。相同的，YI 可以是一個直行向量，它定義一個橫列元素是常數的矩陣。

[XI,YI,ZI] = griddata(x,y,z,xi,yi) 同上，傳回修改過的矩陣 ZI，且傳回從橫列向量 xi 和直行向量 yi 形成的矩陣 XI 和 YI。後者與 meshgrid 傳回的矩陣相同。

[...] = griddata(...,method) 使用特定的修改方法：

'linear'	Triangle-based linear interpolation (預設)
'cubic'	Triangle-based cubic interpolation
'nearest'	Nearest neighbor interpolation
'v4'	MATLAB 4 griddata 方法

method 定義欲符合資料的表面種類。'cubic' 和 'v4' 方法產生平滑的表面，而 'linear' 和 'nearest' 分別在第一個和第零個導數是不連續的。除了 'v4' 之外的其他方法都是以資料的 Delaunay 三角測量(triangulation)為基礎。

Remarks

XI 和 YI 可以是矩陣，在這種情形下 griddata 傳回對應 (XI(i,j),YI(i,j)) 的值。或是，你可以分別傳橫列和直行向量 xi 和 yi。在這種情形下，griddata 把這些向量當作他們是由 meshgrid(xi,yi) 指令產生的矩陣。

Algorithm

griddata(...,'v4')指令使用[1]中敘述的方法。其他方法以 Delaunay 三角測量(triangulation)(see delaunay)為基礎。

Examples

在 ±2.0 中隨機取樣100個點：

rand('seed',0)
x = rand(100,1)*4-2; y = rand(100,1)*4-2;
z = x.*exp(-x.^2-y.^2);

x，y 和 z 現在是包含不一致樣本資料的向量。定義一個一般的格子，然後將資料對應到格子中：

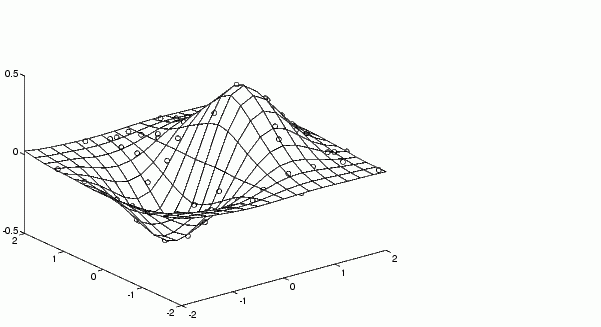
ti = -2:.25:2; 
[XI,YI] = meshgrid(ti,ti);
ZI = griddata(x,y,z,XI,YI);

畫出由不一致的資料點產生的方格化資料：

mesh(XI,YI,ZI), hold
plot3(x,y,z,'o'), hold off

See Also

delaunay, griddata3, griddatan, interp2, meshgrid

References

[1] Sandwell, David T., "Biharmonic Spline Interpolation of GEOS-3 and SEASAT Altimeter Data", Geophysical Research Letters, 2, 139-142,1987.

[2] Watson, David E., Contouring: A Guide to the Analysis and Display of Spatial Data, Tarrytown, NY: Pergamon (Elsevier Science, Inc.): 1992.

grid

griddata3