

| MATLAB Function Reference |   |
Syntax
x = fminsearch(fun,x0) x = fminsearch(fun,x0,options) x = fminsearch(fun,x0,options,P1,P2,...) [x,fval] = fminsearch(...) [x,fval,exitflag] = fminsearch(...) [x,fval,exitflag,output] = fminsearch(...)
Description
fminsearch 從一個初始估量開始,找有多個變數函數的最小值。它們通常被稱為 自然非線性最佳化(unconstrained nonlinear optimization)。
x = fminsearch(fun,x0)
x0 開始,然後在 fun 敘述函數的 x 找局部最小值。x0 可以是一個純量、向量或是矩陣。
x = fminsearch(fun,x0,options)
options 裡的最佳化參數做最小化的動作。
你可以用 optimset 函數定義這些參數。
fminsearch 使用下列 options 結構欄位:
Display |
顯示的等級。'off' 不顯示輸入;'iter' 在每次重複(iteration)時顯示輸出;'final' 只顯示最後結果;'notify' (預設) 只在函數不收斂時顯示輸出。 |
MaxFunEvals |
允許函數求值的最多次數。 |
MaxIter |
允許重複(iteration)的最多次數。 |
TolX |
x 的終結容忍度。 |
x = fminsearch(fun,x0,options,P1,P2,...)
P1、P2、etc.到 fun 函數。如果沒有設定選項,用 options = [] 當作欄位保留。
[x,fval] = fminsearch(...)
傳回目標函數 fun 在解答 x 這一點的值 fval。
[x,fval,exitflag] = fminsearch(...)
傳回描述 fminsearch 跳出狀態的值 exitflag:
| >0 |
表示函數收斂到解答 x。 |
| 0 |
表示到達函數計算次數的最大值。 |
| <0 |
表示函數沒有收斂。 |
[x,fval,exitflag,output] = fminsearch(...)
傳回一個包含最佳化資訊的結構 output:
output.algorithm |
使用的函數 |
output.funcCount |
函數計算的次數 |
output.iterations |
重複(iteration)的次數 |
Arguments
fun 是要最小化的函數。fun 接受一個純量 x 然後傳回一個純量 f,目標函數在 x 做計算。函數 fun 可以當作函數處理定義。
x = fminsearch(@myfun,x0,A,b)
function f = myfun(x) f = ... % Compute function value at x
x = fminsearch(inline('sin(x*x)'),x0,A,b);
Examples
Rosenbrock banana function 是多維最小化的經典測試範例
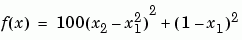
在 (1,1) 有最小值而值是 0。傳統的起始點是 (-1.2,1)。M-檔 banana.m 定義上面的函數。
function f = banana(x)
f = 100*(x(2)-x(1)^2)^2+(1-x(1))^2;
[x,fval] = fminsearch(@banana,[-1.2,1])
x =
1.0000 1.0000
fval =
8.1777e-010
增加第二個參數到 banana.m ,使最小點位置移到點 [a,a^2]。
function f = banana(x,a) if nargin < 2,a = 1; end f = 100*(x(2)-x(1)^2)^2+(a-x(1))^2;
[x,fval] = fminsearch(@banana, [-1.2, 1], ...
optimset('TolX',1e-8), sqrt(2));
設定新的參數到 sqrt(2) ,以比預設更高的精確度在 x 尋找最小值。
Algorithm
fminsearch 使用單純的找尋方法 [1]。這是一個不使用數值或分析梯度的找尋方法。
如果 n 長度是 x,單純的 n-維空間可以用它的 n+1 個不同的向量描述。在二度空間, simplex 是三角形;在三度空間,它是三角錐。在尋找的每一步,會產生在現在 simplex 之內或很接近的新點。在新點的函數值會和在 simplex 的函數值比較,通常,其中一個點會被新的點取代,產生新的單字 simplex。這個步驟會一直重複直到 simplex 的直徑小於定義的容忍度。
Limitations
fminsearch can 通常不連續地處理,尤其是它不是在解答附近發生的話。fminsearch may 只給局部最小。
fminsearch 只最小化實數,就是說,x 必須只包含實數且 f(x) 必須只回傳實數。當 x 有複數變數時,它們必須被分開成實部和虛部。
See Also
fminbnd, optimset, function_handle (@), inline
References
Lagarias, J.C., J. A. Reeds, M. H. Wright, and P. E. Wright, "Convergence Properties of the Nelder-Mead Simplex Method in Low Dimensions," SIAM Journal of Optimization, Vol. 9 Number 1, pp. 112-147, 1998.
 | fmins | fopen |  |