

| MATLAB Function Reference |   |
Complete elliptic integrals of the first and second kind
Syntax
K = ellipke(M) [K,E] = ellipke(M) [K,E] = ellipke(M,tol)
Definition
第一種[1]的 complete elliptic integral 是:

其中 F(the elliptic integral of the first kind)是:
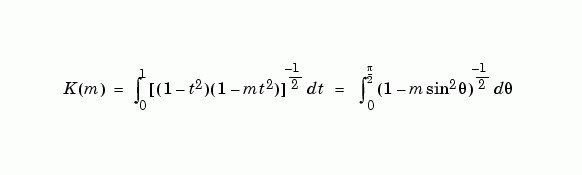
第二種 complete elliptic integral ,

有些 K 和 E 的定義是用絕對值來取代 m 參數。它們之間的關係是:

Description
K = ellipke(M)
傳回對於元素 M 的第一種 complete elliptic integral 值。
[K,E] = ellipke(M)
傳回第一和第二種 complete elliptic integral 的值。
[K,E] = ellipke(M,tol)
以準確度 tol 計算 Jacobian elliptic functions 。預設值是 eps;增加這個值會導致準確度降低,但是計算速度較快。
Algorithm
ellipke 以在 [1]裡17.6節中敘述的算術-幾何平均(arithmetic-geometric mean)計算 complete elliptic integral。它以三個數字開始:

ellipke 以下面的方法依次重複地計算 ai,bi 和 ci:

如果容錯率是 eps,當 cn 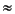 0時,停止計算。第一種 complete elliptic integral 為
0時,停止計算。第一種 complete elliptic integral 為

Limitations
See Also
References
[1] Abramowitz, M. and I.A. Stegun, Handbook of Mathematical Functions, Dover Publications, 1965, 17.6.
 | ellipj | else |  |