

| MATLAB Function Reference |   |
解常微分等式的兩點臨界值問題(two-point boundary value problems (BVPs))
Syntax
sol = bvp4c(odefun,bcfun,solinit) sol = bvp4c(odefun,bcfun,solinit,options) sol = bvp4c(odefun,bcfun,solinit,options,p1,p2...)
Arguments
odefun |
計算微分等式 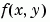 的函數它可以是以下的形式 的函數它可以是以下的形式dydx = odefun(x,y) dydx = odefun(x,y,p1,p2,...) dydx = odefun(x,y,parameters) dydx = odefun(x,y,parameters,p1,p2,...)其中 x 是對應到 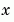 的純量, 的純量,y 是對應到 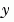 的直行向量。 的直行向量。parameters 是一個未知參數的向量,而 p1,p2,... 是已知參數。輸出 dydx 是一個直行向量。 | |
bcfun |
在臨界值狀態  計算剩餘(residual)的函數。它可以是以下的形式 計算剩餘(residual)的函數。它可以是以下的形式res = bcfun(ya,yb) res = bcfun(ya,yb,p1,p2,...) res = bcfun(ya,yb,parameters) res = bcfun(ya,yb,parameters,p1,p2,...)其中 ya 和 yb 是對應到 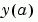 和 和 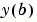 的直行向量。 的直行向量。parameters 是未知參數的向量,而 p1,p2,... 是已知參數。輸出 res 是一個直行向量。 | |
solinit |
有欄位的結構: | |
|
x |
初始 mesh 的 ordered nodes。臨界值狀態被利用在 a = solinit.x(1) 且 b = solinit.x(end)。 |
|
y |
解答的初始預測值,而 solinit.y(:,i) 是在點 solinit.x(i) 的解答預測值。 |
|
parameters |
選擇性的。對未知參數提供初始預測值的向量。 |
|
這個架構可以有任何名稱,但是欄位名稱必須是 x、y 和 parameters。你可以利用幫手函數 bvpinit 來組織 solinit。詳細情形請看 bvpinit 。 | |
options |
選擇性的積分參數。你可以利用 bvpset 函數產生此結構。詳細情形請看 bvpset 。 | |
p1,p2... |
選擇性的。解題器傳到 odefun,bcfun 和其他所有使用者定義在 options 中函數的已知參數。 | |
Description
sol = bvp4c(odefun,bcfun,solinit)
對一個常微分等式系統做積分
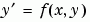
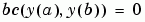
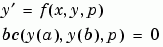
其中 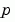 對應到
對應到 parameters。你對 solinit.parameters 中的任何未知參數提供初始預測值 bvp4c。bvp4c 解題器傳回這些未知參數的最終值到 sol.parameters。
bvp4c 產生一個在 [a,b] 間連續且其一次微分也連續的解。用函數 bvpval 和輸出 bvp4c 的 sol 來計算在 [a,b] 間特定點 xint 的解。
yint = bvpval(sol,xint)
x |
bvp4c 選擇的 mesh |
y |
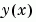 在 在 sol.x mesh 點的近似值 |
yp |
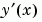 在 在 sol.x mesh 點的近似值 |
parameters |
由 bvp4c 傳回的未知參數值 |
sol 結構可以有任何名稱,而 bvp4c 產生的欄位 x、y、yp 和 parameters。
sol = bvp4c(odefun,bcfun,solinit,options)
像之前一樣解題器,而預設的積分屬性被 bvpset 函數產生的結構 options 值取代。詳細情形請看 bvpset。
sol = bvp4c(odefun,bcfun,solinit,options,p1,p2...)
傳常數的 已知 參數,p1、p2、...,到 odefun、bcfun,和其他所有使用者定義在 options 的函數。如果沒有選項被設定,則把 options = [] 當作欄位保留。
Examples
Example 1. 臨界值問題可以有多組解,而初始預測值的其中一個目的就是要指出哪一組解是你要的。兩次微分等式
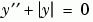
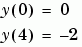
先用 bvp4c 解這個問題,微分等式必須用兩個一次 ODEs 的系統表示

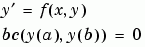
函數 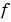 和臨界狀態
和臨界狀態 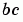 都被用 MATLAB 寫成函數
都被用 MATLAB 寫成函數 twoode 和 twobc。
function dydx = twoode(x,y)
dydx = [ y(2)
-abs(y(1))];
function res = twobc(ya,yb)
res = [ ya(1)
yb(1) + 2];
一個預測架構(guess structure)包含 [0,4] 間五條空間相等的初始格線與一個常數值  和
和 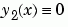 的預測,以下面的形式產生
的預測,以下面的形式產生
solinit = bvpinit(linspace(0,4,5),[1 0]);
sol = bvp4c(@twoode,@twobc,solinit);
y = bvpval(sol,linspace(0,4)); plot(x,y(1,:));
solinit = bvpinit(linspace(0,4,5),[-1 0]);
Example 2. 這個臨界值問題包含未知參數。這個工作就是去計算 Mathieu's equation 的第四個特徵值(eigenvalue) 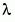 (
(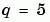 )
)
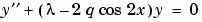
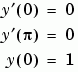
我們可以很方便的使用副函數來安置所有需要被 bvp4c 用到的函數在一個 M-檔。
function mat4bvp
lambda = 15;
solinit = bvpinit(linspace(0,pi,10),@mat4init,lambda);
sol = bvp4c(@mat4ode,@mat4bc,solinit);
fprintf('The fourth eigenvalue is approximately %7.3f.\n',...
sol.parameters)
xint = linspace(0,pi);
Sxint = bvpval(sol,xint);
plot(xint,Sxint(1,:))
axis([0 pi -1 1.1])
title('Eigenfunction of Mathieu''s equation.')
xlabel('x')
ylabel('solution y')
% ------------------------------------------------------------
function dydx = mat4ode(x,y,lambda)
q = 5;
dydx = [ y(2)
-(lambda - 2*q*cos(2*x))*y(1) ];
% ------------------------------------------------------------
function res = mat4bc(ya,yb,lambda)
res = [ ya(2)
yb(2)
ya(1)-1 ];
% ------------------------------------------------------------
function yinit = mat4init(x)
yinit = [ cos(4*x)
-4*sin(4*x) ];
微分等式(轉換成一個一次系統)和臨界狀態分別被副函數 mat4ode 和 mat4bc 所描述。因為有未知參數,所以即使某些參數不會用到,這些函數都必須接受三個輸入參數。
預測結構 solinit 是由 bvpinit 產生。 解答的初始預測是以函數 mat4init 提供。我們選擇 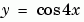 因為它滿足臨界狀態且有正確的性質行為(正確的正負號變換次數)。在呼叫
因為它滿足臨界狀態且有正確的性質行為(正確的正負號變換次數)。在呼叫 bvpinit時,第三個參數(lambda = 15) 提供一個初始預測值給未知參數 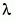 。
。
在問題被 bvp4c 解決之後,sol.parameters 欄位傳回值 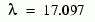 ,而且圖形顯示特徵函數和這個特徵值相關。
,而且圖形顯示特徵函數和這個特徵值相關。
Algorithms
bvp4c 是三步驟的 Lobatto IIIa formula 有限積分。組合公式和組合多項式在 [a,b] 間提供一致的四次準確度 C1-連續解。格線(mesh)選擇和誤差控制都是以連續解的剩餘(residual)為基礎。
See Also
@ (function_handle), bvpget, bvpinit, bvpset, bvpval
References
[1] Shampine, L.F., M.W. Reichelt, and J. Kierzenka, "Solving Boundary Value
Problems for Ordinary Differential Equations in MATLAB with bvp4c,"
available at ftp://ftp.mathworks.com/pub/doc/papers/bvp/.
 | builtin | bvpget |  |