5-7 嚙踝蕭嚙踝蕭嚙踝蕭嚙踝蕭嚙踝蕭

Old Chinese version

貝式分類法（Bayes classifier）乃是根據貝氏定理（Bayes' theorem）為基礎，用以判斷未知類別的資料應該最接近哪一個類別。整個貝式分類法的目標是希望能透過機率統計的分析，達到最小誤差的一種分類方式。

假設現在存在某個特徵值x及某個類別 C，P(x) 表示該特徵值出現的估測機率，P(C) 表示任意藉由亂數取出的特徵值恰巧落於類別 C 的機率，我們將之稱為事前機率（prior probability），則根據條件機率（conditional probability），貝式定理可以表示為：

P(C|x) = P(C∩x)/P(x) = P(C)P(x|C)/P(x) 其中，P(C|x) 表示 x 該特徵值出現時，又恰巧落於類別C的機率，我們將他稱為事後機率（posterior probability）；至於 P(x|C) 則表示落於類別 C 中的資料點中，又恰巧發生特徵值為 x 的機率。

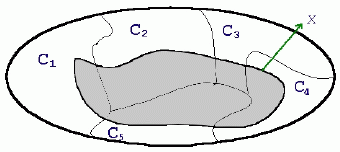
假設該空間中可能出現的類別總共有 k 個 {C₁, C₂, …, C_k}，且每個類別彼此均互斥，則我們可以得到下列方程式：

P(x)	=	P(x∩C1) + P(x∩C2) + ... + P(x∩Ck)
	=	P(C1)P(x|C1) + P(C2)P(x|C2) + ... + P(Ck)P(x|Ck)

請參考下列獨立事件機率分佈示意圖：

由前述方程式，我們可以得知： P(C_i|x) = P(C_i)P(x|C_i)/P(x) 若使用上述方程式，我們可以得到應用於k個類別的貝式定理：

P(Ci|x) =	P(Ci)P(x|Ci)
	──────────────────────
	P(C1)P(x|C1) + P(C2)P(x|C2) + ... + P(Ck)P(x|Ck)

當我們要判斷某特徵值x究竟屬於哪一個類別時，則我們僅需估算類別Ci與類別Cj之間的相似率（likelihood ratio）R：

R =	P(Ci|x)	=	P(Ci)P(x|Ci)
	──────		──────
	P(Cj|x)		P(Cj)P(x|Cj)

假如 R > 1，表示 x 比較偏向類別 C_i；反之，假如 R < 1，表示 x 比較偏向類別 C_j。

在實際運算時，P(C_i) 是第 i 類資料佔總樣本資料的機率，而 P(x|C_i) 則是由第i類資料點所估測出來的一個機率密度函數（例如高斯分佈）。

我們可以將貝式定理再往下推演，假如現在判斷的條件不止一個特徵值，而是一組彼此互相獨立的特徵值 (x₁, x₂, …, x_d)，則當給定某個類別 C_i 時，其條件機率可以表示為：

P(x₁, x₂, …, x_d|C_i) = P(x₁|C_i)P(x₂|C_i) ... P(x_d|C_i) 如果將方程式（3-2.6）的結果代入方程式（3-2.4）中，則我們可以得到k個類別中，包含d個特徵值的貝式定理：

P(Ci|x1, x2, …, xd) =	P(Ci) P(x1|Ci)P(x2|Ci) ... P(xd|Ci)
	────────────────
	Si=1k P(Ci) P(x1|Ci)P(x2|Ci) ... P(xd|Ci)

---

Data Clustering and Pattern Recognition (資料分群與樣式辨認)