SC Homework 6
Due date: 20160605 23:59:59
Note that the description of this homework may be lengthy, but the concept is pretty straightforward. If you have questions about this homework, please come to my office hour at 5pm, 5/25 (Wed), at CSIE basement.
Query by Singing/Humming
Outlines
 Problem definition
Problem definition
Dynamic programming (DP) is a very important and useful method for sequence comparision. It has been used extensively in speech recognition, natural language processing, music analysis, and a variety of other areas. In this homework, we shall explore the use of DP for query by singing/humming (QBSH), which is an interesting paradigm of music information retrieval. (For simplicity, we shall assume our QBSH system always starts the comparison from the beginning of a song.)
In particular, you need to find the alignment between the pitch vector of human's singing and the note vector of a given melody, both in the unit of semitone or MIDI number. The correspondence between MIDI numbers and piano keyboard can be found here. Moreover,
- Here is a typical singing clip and its corresponding pitch vector which can be played here.
- The note vector is the music notes corresponging to the intended song of the singing. For simplicity, there no duration information in the vector. Therefore for the song of "Twinkle twinkle little star", here is the music note vector for the first two phrases: [60 60 67 67 69 69 67 65 65 64 64 62 62 60].
Given a pitch vector and a note vector, your mission is to find an optimum mapping to assign each pitch point to a music note, such that the total distance is minimized. To be more specific, let's use the following notation:
- $p(i)$ is element $i$ of the pitch vector, where $0 \leq i \leq m-1$.
- $q(j)$ is element $j$ of the note vector, where $0 \leq j \leq n-1$.
The alignment path can be denoted by its coordinates, that is, $\{(0, u_0), (1, u_1), (2, u_2), ..., (m-1, u_{m-1})\}$, where $u_k, k=0, 1, \cdots, m-1$ are indices into the note vector with the following constraints:
- $u_0=0$.
- $u_0 \leq u_1 \leq u_2 \cdots \leq u_{m-1}$.
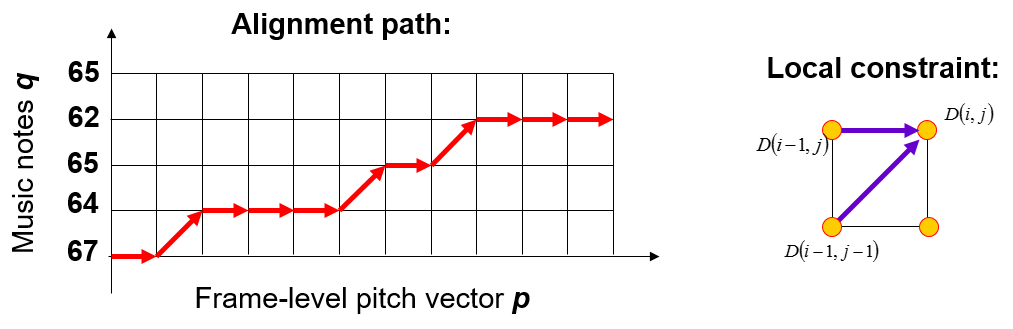
For instance, the alignment path of the above figure is ${(0, 0),(1, 0),(2, 1),(3, 1),(4, 1),(5, 1),(6, 2),(7, 2),(8, 3),(9, 3),(10, 3),(11, 3)}$, with $m=12$ (the length of $p$) and $u_{m-1}=3$ (the last index of music note that have at least one pitch point being assigned to). In other words:
- p(0) and p(1) are assigned to q(0).
- p(2), p(3), p(4) and p(5) are assigned to q(1).
- p(6) and p(7) are assigned to q(2).
- p(8), p(9), p(10) and p(11) are assigned to q(3).
The distance between a pitch vector $p$ and note vector $q$ can then be defined as follows:
$$
D(p, q)=\min_{u_0, u_1, ... u_{m-1}}\sum_{i=0}^{m-1} |p(i)-q(u_i)|,
$$
subject to $u_0=0$ and $u_0 \leq u_1 \leq u_2 \cdots \leq u_{m-1}$.
 Suggested approach
Suggested approach
Based on the above description, we can solve the task using DP. The 3-step formula for DP can be described as follows:
- Optimum-value function $D(i,j)$ is defined as the minimum distance between $p(0:i)$ and $q(0:j)$.
- Recurrent equation for $D(i,j)$ is shown next, with $i>0$ and $j>0$:
$$
D(i,j)=|p(i)-q(j)|
+\min
\left\{
\begin{matrix}
D(i-1,j)\\
D(i-1, j-1)\\
\end{matrix}
\right.
$$
(See the local constraint in the previous figure.) Please derive the recurrent equation when $i=0$ or $j=0$ by yourself.
The boundary condition is $D(0, 0)=|p(0)-q(0)|$.
-
Answer to the original task:
$$
dist(p, q) = \min_{0\leq j \leq n-1}D(m-1, j).
$$
 Input/output formats
Input/output formats
- Input format:
m ← The number of elements of the pitch vector
$p_0$ $p_1$ $p_2$ . . . . . . $p_{m-1}$ ← the $m$ elements of the pitch vecotr
n ← The number of elements of the note vector
$q_0$ $q_1$ $q_2$ . . . . . . $q_{n-1}$ ← the $n$ elements of the note vecotr
- Output format:
distance ← The overall minimized distance
$s_0$ $s_1$ $s_2$ $s_3$ $s_4$ ... $s_{u_{m-1}}$ ← Starting index of pitch vector being assigned to each music notes
where
- $s_0$ to $s_1-1$ are the indices of the pitch vector being assigned to note 0. ($s_0$ is always 0.)
- $s_1$ to $s_2-1$ are the indices of the pitch vector being assigned to note 1.
- $s_2$ to $s_3-1$ are the indices of the pitch vector being assigned to note 2.
- ...
- $s_{u_{m-1}}$ to $m-1$ are the indices of the pitch vector being assigned to note $u_{m-1}$, where $u_{m-1}+1$ is the total number of music notes that have at least one pitch point being assigned to.
Take the alignment path shown in the previous figure as an example, the second line of the output file should be "0 2 6 8", with $u_{m-1}=3$.
 Requirements & suggestions
Requirements & suggestions
- You can safely assume $m<1000$ and $n<100$. (This is irrelevant if you use dynamic memory allocation for creating the matrix.)
- If there are repeated notes, the optimal path might not be unique. As a result, TA's judge system will check your output based on the returned minimum distance. If the deviation between your distance and TA's distance is less than 1, it'll be considered as correct.
- Your best bet is to use DP for the homework. Of course, you can still use other approaches if they are as efficient as DP.
- The alignment path shown in the previous plot is based on X-Y mode, which is commonly used in the Cartesian coordinate system. If you want to adopt I-J mode (commonly used in matrix indexing), you can simply rotate the plot by 90-degree clockwise.
- My test using a pitch vector of 207 elements and a note vector of 14 elements takes only 0.000154 second on my i7-5700HQ notebook PC.
As a result, a time limit of 0.01 second will be imposed on your program for each task of a similar size. Your score is zero if the time limit is exceeded.
- The process of converting a singing clip into its pitch vector is call pitch tracking, which is out of the scope of this class.
- If you are interested in trying out QBSH systems, try our lab's system at http://mirlab.org/demo/miracle.
- As usual...
- Your program should take the input from the standard input and send the output to the standard output.
- You need to write the program from scratch. You cannot use any open-source or readily available solvers.
 Test set
Test set
Each test case is shown below. You can download the whole test set at this link. Note that the pitch vector is actually obtained from twinkle_twinkle_little_star.wav, except that we have performed fine tuning to take key transposition into consideration. (Don't worry, you can still do the homework if you don't know what key transposition is.) So these 48 cases corresponding to the comparison between the pitch vector and 48 songs in a QBSH system. You can see that the minimum distance of these 48 cases occurs when the MIDI file is "twinkle_twinkle_little_star.MID", indicating this is a successful retrieval based on the given pitch vector. The plot of distances to 48 MIDI files are shown next (where "小星星" is actually the song "Twinkle Twinkle Little Star"):
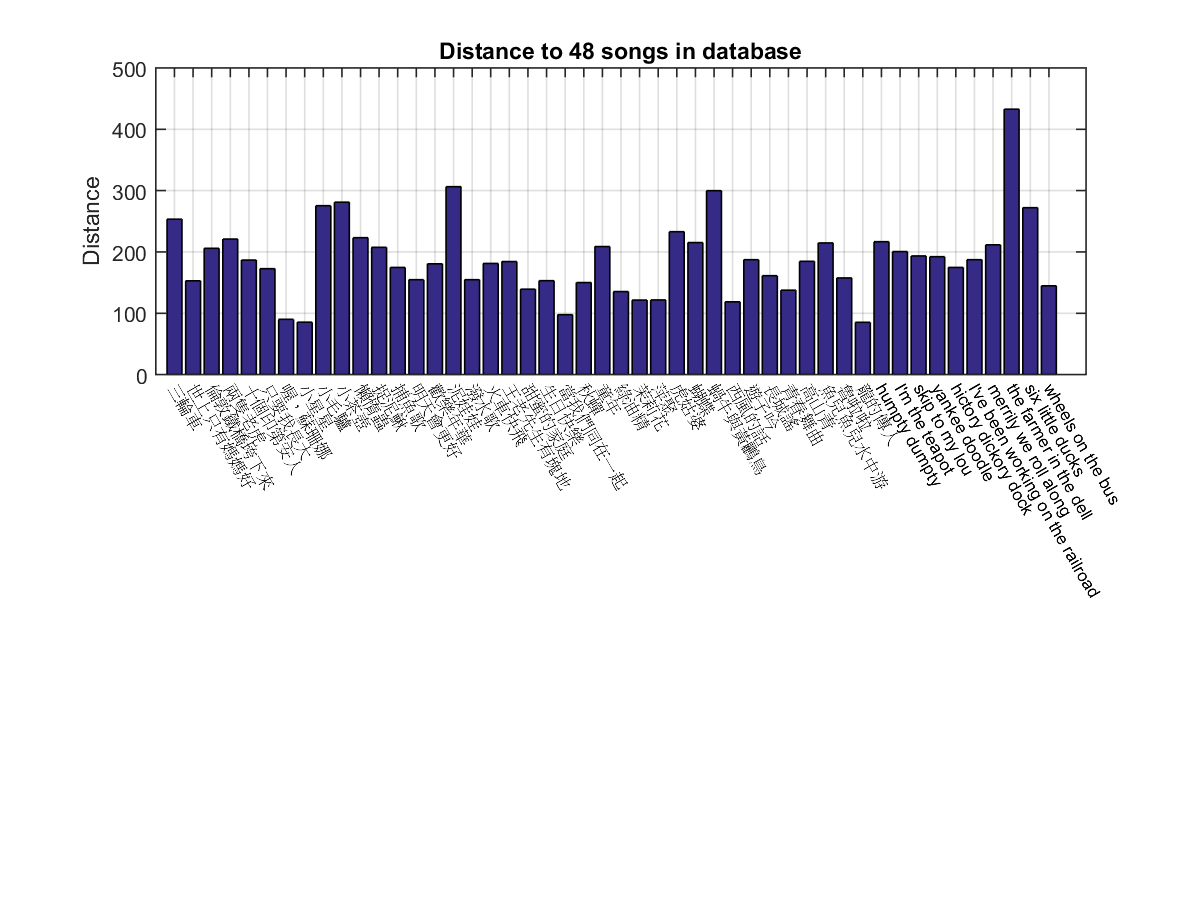
For each test input/output, you can see corresponding debugging info, which can be used to verify the corresponding results. More specifically,
- The MIDI file is where the note vector for each test case is from.
- The alignment path shows the pitch vector and the note vector, and the optimum path based on DP.
- The plot for pitch vector ($p(i), i=0, 1, \cdots, m-1$) and its induced version ($q(u_i), i=0, 1, \cdots, m-1$) gives you an idea as how similar they are.
Here is the list of each test case.
 Slides
Slides
Slides for this homework (recording to be uploaded soon)
 Submission guidelines
Submission guidelines
Please submit your code with GitHub as directed in the GitHub submission guide. Your directory structure (under GitHub repository) should be:
- hw6/*, your source code.
- hw6/Makefile, where the TAs can use the command ”make” on CSIE R217 linux machines to compile your code, and ”make run” to run your program.
You have to make sure your code can be compiled on CSIE R217 linux machines with your Makefile and run normally since we will test your program on CSIE R217 linux machines.

 Problem definition
Problem definition Problem definition
Problem definition
 Suggested approach
Suggested approach Input/output formats
Input/output formats Requirements & suggestions
Requirements & suggestions Test set
Test set
 Slides
Slides Submission guidelines
Submission guidelines