15-1 嚙踝蕭嚙踝蕭犰V嚙緹嚙踝蕭嚙稽嚙緘

物件導向程式設計（Object Oriented Programming，簡稱 OOP）是目前軟體設計的潮流，一般高階程式語言都支援 OOP 的概念，例如 C++、JavaScript、C#、Java 等等，MATLAB也不例外，因此本章將說明 MATLAB 在 OOP 概念下的撰寫方式，以便簡化軟體的抽象概念、提高程式碼的可讀性與重複使用性，並讓軟體的管理更加簡潔透明。

首先，我們要能夠建立一個類別（Class），並經由此類別建構出實際的物件（Object），如此才能進而使用物件的各種方法來達成應用程式的最後目的。類別是一個虛擬的概念，例如「人」可以看成是一個類別，包含各種性質的定義（例如名字、性別、身高、體重等），但是物件則是實際由類別產生的實體，例如「孔子」或是「金城武」就是由「人」所產生的實體，此實體就會有確切的名字、性別、身高、體重等性質。

以下我們將以先多項式為範例，來說明 MATLAB 如何實作 OOP 的基本概念。MATLAB 建立類別的方式是直接產生一個以「@」為開頭的資料夾，所有與此類別相關的函式都放在此資料夾之下，例如，在本章的範例程式目錄中，你可以發覺有一個目錄的名稱是 @polynom，這就是對應到多項式類別的目錄，所有相關的函式（也就是物件的方法）也都放在這個目錄下。

Hint

你必須將包含此 @polynom 的上層目錄加到 MATLAB 的搜尋路徑後，才可以在任意處使用與 polynom 相關的物件或方法。

接著我們要定義建構函式（Constructor）以便產生多項式物件，此建構函式的名稱必須和類別的目錄名稱一樣（但不包含 “@”），以多項式物件而言，建構函式的名稱就是 polynom.m，其內容如下：

Example 1: 15-物件導向程式設計/@polynom/polynom.m

function poly = polynom(vec) %POLYNOM Polynomial class constructor % poly = POLYNOM(vec) creates a polynomial object from the given vector vec % which contains the coefficients of the descending-order polynomial. if isa(vec, 'polynom') % 若 vec 已經是 polynom 物件，則直接設定成輸出 poly = vec; else poly.c = vec(:).'; % 將向量設定成 poly 的係數 poly = class(poly, 'polynom'); % 將 poly 加持成 polynom 物件 end

從上述程式碼可以看出：

如果輸入是一個向量，這就是多項式的係數（降冪排列），我們將此係數設定給 poly.c，最後使用 class 函式將 poly 變數加持成 polynom 物件。

如果輸入 vec 已經是一個 polynom 物件，則直接輸出此物件。（isa(vec, ‘polynom’) 用來檢查 vec 是否是一個 polynom 物件。）

由上述程式碼也可以看出，poly 原來是一個結構變數，具有一個欄位 c 來儲存多項式的係數，但是一旦經由 poly = class(poly, ‘polynom’) 來將之加持成為物件之後，我們在外部並無法經由 poly 物件來取得 c 欄位值，而必須定義其他方法來取得資料（詳見後述），這也是 OOP 的基本精神：所有物件的性質是無法任意開放給外界環境，而必須經由與此物件相關的特定函式來取得。

有了此建構函式，我們就可以建構一個多項式物件，但為了比較能夠優雅地展示此物件的內容，我們可以寫一個顯示函式 display.m 來顯示此多項式，此顯示函式的名稱必須固定為 display.m，且必須位於 @polynom 目錄下，一旦 MATLAB 需要顯示此多項式物件，即會自動呼叫此函式，其內容如下：

Example 2: 15-物件導向程式設計/@polynom/display.m

function display(poly) % POLYNOM/DISPLAY Display of a polynom disp(' '); disp([inputname(1),' = ']) disp(' '); disp([' ', polyAsString(poly)]) disp(' ');

上述函式呼叫了另一個函式 polyAsString.m，其功能是將多項式轉為字串形式，便於觀看，程式碼如下：

Example 3: 15-物件導向程式設計/@polynom/polyAsString.m

function s = polyAsString(poly) % POLYNOM/POLYASSTRING String representation of a polynom degree=length(poly.c)-1; s = sprintf('%d*x^%d', poly.c(1), degree); for i=degree-1:-1:0 coef = poly.c(degree-i+1); if coef >=0 s=sprintf('%s + %d*x^%d', s, coef, i); else s=sprintf('%s - %d*x^%d', s, -coef, i); end end

一旦有了建構函式 polynom.m 和顯示函式 display.m 後，我們就可以直接產生一個多項式物件並顯示此物件，如下：

Example 4: 15-物件導向程式設計/test01.m

p = polynom([3 4 2 1]) p = 3*x^3 + 4*x^2 + 2*x^1 + 1*x^0

在 MATLAB 命令視窗所產生的字串，即是由顯示函式 display.m 所產生的結果。（當然，這個字串可能不是很符合一般多項式的寫法，讀者可以自行修改 display.m，使其產生的字串更漂亮一些。）

Hint

上述顯示函式屬於一般物件的內建顯示函式，其它的與物件相關的函式還有加、減、乘、除等基本運算元，請見下一節說明。

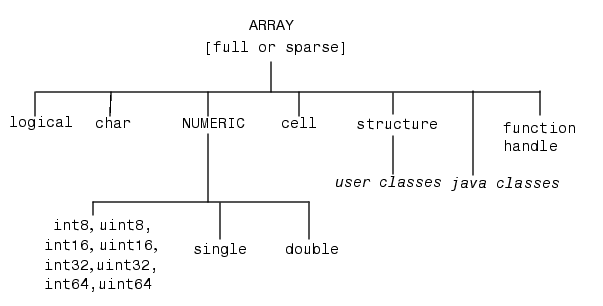
由使用者所定義的類別，事實上是屬於 MATLAB 資料類別階層的一部份，MATLAB資料類別階層如下：

其中的 user classes 就是由使用者定義的類別，它繼承了 structure 類別的相關特性。由上述資料類別階層，我們可以瞭解資料類別之間的從屬關係。

一般而言，支援 OOP 的程式語言大略都有下述基本功能：

1. 函式及運算元的重載 (Function and operator overloading)：根據特定的類別或物件，你可以產生各種方法。對應這些方法的函式名稱可以和 MATLAB的內建函式一樣，但MATLAB會根據輸入參數的資料型態，來決定呼叫哪一種函式。
2. 資料和方法的封裝 (Encapsulation of data and methods)：所有物件的性質，並無法從外界直接取得或修改，必須經由此物件所提供的方法，才能取得或修改此物件的性質。這樣可以保證物件的完整性，不會誤遭讀取或修改。此外，物件的方法也只適用於物件本身，確保不會誤用。
3. 繼承 (Inheritance)：類別可以有繼承關係，例如「人」是一種類別，而「學生」則是「人」的子類別，因此「學生」類別可以繼承「人」類別的性質和方法。善用繼承，可讓我們對真實世界的描述更加完善。
4. 聚合 (Aggregation)：我們可以使用聚合的概念來定義某些類別，經由這種類別所產生的物件，可以包含其他物件。例如，「學生」所修的「課程」，就可以由聚合來定義。

以下幾節將說明 MATLAB 對這些 OOP 特性的實作和範例。

---

MATLAB程式設計：進階篇