一般「多輸入、單輸出」的線性迴歸數學模型可寫成
$$ y = f(\mathbf{x}) = \theta_1f_1(\mathbf{x}) + \theta_2f_2(\mathbf{x}) + \cdots + \theta_nf_n(\mathbf{x}) $$其中 $\mathbf{x}$ 為輸入(長度為 $m$ 的向量),y 為輸出(純量),$\theta_1$、$\theta_2$、$\cdots$、$\theta_n$ 為可變的未知參數,$f_i(\mathbf{x}), i=1$ to $n$ 則是已知的函數,稱為基底函數(Basis Functions)。假設所給的資料點為 $(\mathbf{x}_i, y_i), i=1 \cdots m$,這些資料點稱為取樣資料(Sample Data)或訓練資料(Training Data),將這些資料點帶入模型後可得: $$ \left\{ \begin{matrix} y_1 & = & f(\mathbf{x}_1) & = & \theta_1f_1(\mathbf{x}_1) + \theta_2f_2(\mathbf{x}_1) + \cdots + \theta_nf_n(\mathbf{x}_1) \\ \vdots & = & \vdots & = & \vdots \\ y_m & = & f(\mathbf{x}_m) & = & \theta_1f_1(\mathbf{x}_m) + \theta_2f_2(\mathbf{x}_m) + \cdots + \theta_nf_n(\mathbf{x}_m) \\ \end{matrix} \right. $$
或可表示成矩陣格式:
$$ \underbrace{ \left[ \begin{matrix} f_1(\mathbf{x}_1) & \cdots & f_n(\mathbf{x}_1) \\ f_1(\mathbf{x}_2) & \cdots & f_n(\mathbf{x}_2) \\ \vdots & \vdots & \vdots\\ f_1(\mathbf{x}_m) & \cdots & f_n(\mathbf{x}_m) \\ \end{matrix} \right] }_\mathbf{A} \underbrace{ \left[ \begin{matrix} \theta_1\\ \vdots\\ \theta_n\\ \end{matrix} \right] }_\mathbf{\theta} = \underbrace{ \left[ \begin{matrix} y_1\\ y_2\\ \vdots\\ y_m\\ \end{matrix} \right] }_\mathbf{y} $$由於在一般情況下,$m>n$(即資料點個數遠大於可變參數個數),因此上式無精確解,欲使上式成立,須加上一誤差向量 $\mathbf{e}$: $$ \mathbf{A}\mathbf{\theta}=\mathbf{y}+\mathbf{e} $$ 平方誤差則可寫成
$$ E(\mathbf{\theta})=\|\mathbf{e}\|^2=\mathbf{e}^T\mathbf{e}= (\mathbf{A}\mathbf{\theta}-\mathbf{y})^T (\mathbf{A}\mathbf{\theta}-\mathbf{y}) $$直接取 $E(\mathbf{\theta})$ 對 $\mathbf{\theta}$ 的偏微分,並令其等於零,即可得到一組 $n$ 元一次的線性聯立方程式,若使用矩陣運算來表示,$\mathbf{\theta}$ 的最佳值可以表示成 $$ \hat{\mathbf{\theta}} = (\mathbf{A}^T\mathbf{A})^{-1}\mathbf{A}^T\mathbf{y} $$ (有關上式的推導,可見本章最後一小節的說明。)
在實作上,我們可以直接使用 MATLAB 的「左除」來算出 $\mathbf{\theta}$ 的最佳值,即 $\hat{\mathbf{\theta}} = \mathbf{A}$\$\mathbf{y}$。
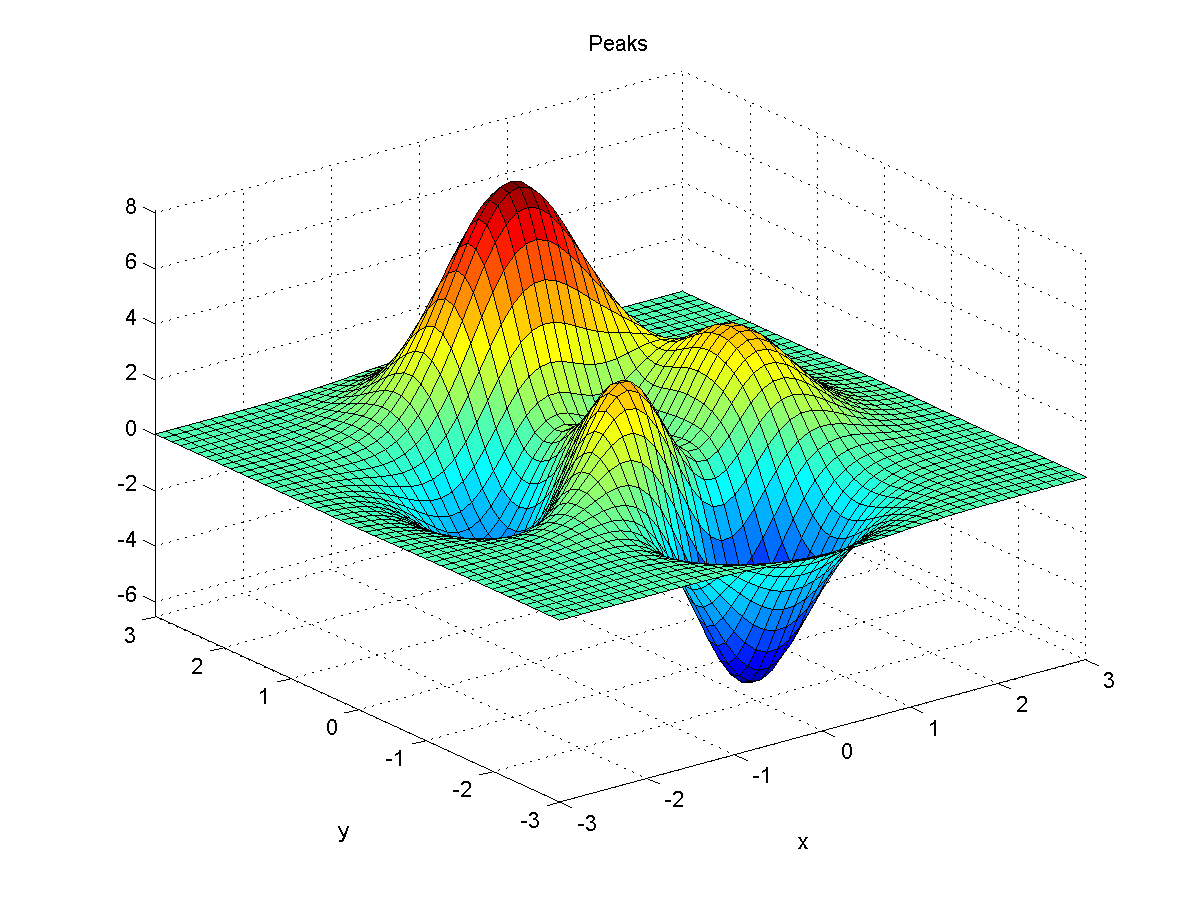
以下以“ peaks ”函數為例,來說明一般的線性迴歸。若在 MATLAB 下輸入 peaks,可以畫出一個凹凸有致的曲面,如下:
此函數的方程式如下:
$$ z = 3(1-x)^2 e^{-x^2-(y+1)^2}-10\left(\frac{x}{5}-x^3-y^5\right) e^{-x^2-y^2}- \frac{1}{3} e^{-(x+1)^2-y^2} $$在下列說明中,我們假設:
- 數學模型的基底函數已知
- 訓練資料包含正規分佈的雜訊
因此上述函數可寫成:
$$ \begin{array}{rcl} z & = & 3(1-x)^2 e^{-x^2-(y+1)^2}-10\left(\frac{x}{5}-x^3-y^5\right) e^{-x^2-y^2}- \frac{1}{3} e^{-(x+1)^2-y^2} + noise\\ & = & 3 f_1(x, y) - 10 f_2(x, y) - \frac{1}{3} f_3(x, y) + noise\\ & = & \theta_1 f_1(x, y) + \theta_2 f_2(x, y) + \theta_3 f_3(x, y) + noise\\ \end{array} $$其中我們假設 $\theta_1$、$\theta_2$ 和 $\theta_3$ 是未知參數,$noise$ 則是平均為零、變異為 1 的正規分佈雜訊。例如:如果要取得 100 筆訓練資料,可使用下列範例:
在上例中,randn 指令的使用即在加入正規分佈雜訊。上圖為我們收集到的訓練資料,由於雜訊很大,所以和原先未帶雜訊的圖形差異很大。現在我們要用已知的基底函數,來找出最佳的 $\theta_1$、$\theta_2$ 和 $\theta_3$,範例如下:
由此找出的 $\mathbf{\theta}$ 值和最佳值 $\left(3, -10, -\frac{1}{3} \right)$ 相當接近。根據此參數,我們可以輸入較密的點,得到迴歸後的曲面,請見下列範例:
在上圖中,可知迴歸後的曲面和原先的曲面相當接近。最主要的原因是:我們猜對了基底函數(或是更正確的說,我們偷看了正確的基底函數),因此得到非常好的曲面擬合。一般而言,若不知正確的基底函數而胡亂選用,很難由 3 個可變函數達到 100 個資料點的良好擬合。
在上例中我們曾在資料點加入正規分佈(Normal Distributed)的雜訊。事實上,只要基底函數正確,而且雜訊是正規分佈,那麼當資料點越來越多,上述的最小平方法就可以逼近參數的真正數值。
MATLAB程式設計:進階篇