Chapter 6: Exercises

Part 1

  1. 請寫一個 MATLAB 程式碼 testMat01.m，請依下列步驟進行此作業：
    1. 使用 randn 指令產生一個 10×10 的矩陣 A。
    2. 計算 B=(A+A')/2。請注意，B 一定是一個對稱矩陣。
    3. 計算矩陣 B 的固有向量 e1, e2, ... e10。
    4. 驗證在 i 不等於 j 的情況下，ei 和 ej 的內積必定為零。
  2. 我們可用數學證明：一個方陣的行列式值會等於其固有值的乘積。請寫一個 MATLAB 程式碼 testEig01.m，隨意產生 10 個 100×100 的方陣來驗證上述定理。
  3. 我們可用數學證明：一個方陣的主對角線的元素和，會等於其固有值的和。請寫一個 MATLAB 程式碼 testEig02.m，隨意產生 10 個 100×100 的方陣來驗證上述定理。
  4. Please use 3 lines of MATLAB statements to solve the following simultaneous linear equations: $$ \left\{ \begin{matrix} x+y+z=1\\ 3x-y-3z=4\\ x+5y-9z=0\\ \end{matrix} \right. $$
  5. 請寫一個 MATLAB 程式碼 lse01.m，使用 MATLAB的「左除」找出一點 P，使得 P 到下列三條直線的距離平方和為最小： $$ \left\{ \begin{matrix} 2x-y = 2\\ x-2y = -2\\ x+y = 1\\ \end{matrix} \right. $$ 請問 P 值為何？此時最小距離平方和是多少？
  6. 請寫一個 MATLAB 程式碼 lse02.m，採用 MATLAB 的「左除」運算，找出下列聯立方程式的最小平方解： $$ \left\{ \begin{matrix} 3x+2y = 1\\ x+3y = 4\\ 4x+2y = 3\\ x-y = 6\\ \end{matrix} \right. $$ 此時最小平方誤差是多少？

Part 2

  1. Definition of eigenvalues and eigenvectors: What is the definition of eigenvalues and eigenvectors of a square matrix A?
  2. Formula for eigenvalue decomposition: What is the formula for eigenvalue decomposition? (Please clearly define your notation.)
  3. 試用 MATLAB的「左除」運算，找出最接近下列五點的最小平方三次多項式：
    (1, 5) (2, 3) (3, 4) (4, 7) (5, 2)
    請畫出此多項式及這五點資料。（請使用 MATLAB的「左除」或「反斜線」，而不要直接使用 polyfit 指令。）
  4. Sum of squared distances between a point and multiple planes: 請使用 MATLAB的「左除」找出空間中的一點 P，使得 P 到下列 4 個平面的距離平方和為最小： $$ \left\{ \begin{matrix} 2x-y+2z & = & 2\\ x-2y-2z & = & -2\\ x+y+z & = & 1\\ z & = & 5\\ \end{matrix} \right. $$ 請問 P 值為何？此時最小距離平方和是多少？
  5. Eigenvalue of same-column-sum matrix: Suppose that a square matrix A has its column sums all equal to k. Prove that k is an eigenvalue of A.
  6. Power method to compute page rank: As described in our slides, we can use the power method to find the page rank of a given connectivity matrix. That is, we can repeat $\mathbf{x}=A*\mathbf{x}$ until $\mathbf{x}$ converges to find the page rank, where $A$ is the transition probability matrix derived from the connectivity matrix. Write a function pageRankByPower.m to return the page rank, with the following usage:
    [pagerank, iterCount]=pageRankByPower(G, p),
    where
    • G: the given connectivity matrix
    • p: the given probability of following a link in a page
    • pagerank: the returned page rank
    • iterCount: the iteration count of the power method
    More specs are as follows:
    • Note that you can only use the power method to implement this function.
    • The initial guess of the page rank should be a probability vector of uniform distribution.
    • The maximum iteration count is 100. Once the maximum iteration count is reached, the current page rank is returned immediately.
    • The iteration stops whenever max(abs(pr-prprev)) < eps, where pr is the current page rank and prprev is the page rank obtained at previous iteration.
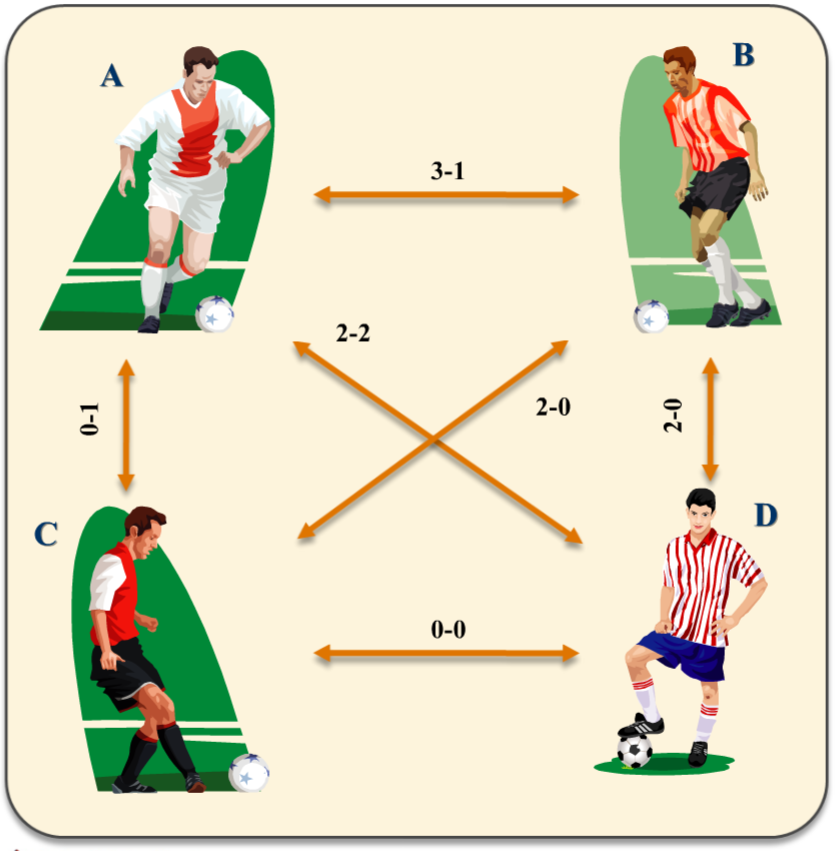
    You can download the p-file pageRankByPower.p to test your function. Here is a test script with several test cases:

    Example 1: 06-線性代數/pageRankByPower01.mG=[0 0 0 1 0 1;1 0 0 0 0 0;0 1 0 0 0 0;0 1 1 0 0 0;0 0 1 0 0 0;1 0 1 0 0 0]; p=0.85; [pageRank1, iterCount1]=pageRankByPower(G, p) G=[1 0 0 0 0 0 0 1 0 0;1 1 0 0 0 0 0 0 1 0;0 1 1 0 0 0 0 1 0 0;1 0 1 0 0 0 0 0 0 0;0 1 0 0 0 0 1 1 1 0;0 0 0 1 0 0 1 0 0 0;0 0 0 0 0 1 0 0 0 0;0 1 0 0 0 0 0 0 0 0;1 0 0 1 0 0 0 0 0 0;1 1 0 0 0 0 0 0 0 0]; p=0.9; [pageRank2, iterCount2]=pageRankByPower(G, p) pageRank1 = 0.3210 0.1705 0.1066 0.1368 0.0643 0.2007 iterCount1 = 64 pageRank2 = 0.0541 0.0929 0.1110 0.0899 0.1683 0.1417 0.1578 0.0470 0.0805 0.0567 iterCount2 = 74

  7. Ranking of sports teams: In this assignment, we shall use the concept of Google's PageRank for team ranking. During a sports season, we have four teams with the following result, with "m-n" indicating that there are m+n games between two teams, with m winning games for the left team and n winning games for the right team. (For instance, 3-1 between teams A and B indicates that A has 3 winning games while B has 1.)

    We shall use the following steps to explain how to find the strength (or team rank) of each team.
    1. We can use a matrix GD to respresent the result of "difference in winning games": GD = [ 0 2 1 0 -2 0 -2 -2 -1 2 0 0 0 2 0 0]; where GD(i,j) is the no. of difference of winning games between team i and team j. For instance, GD(2,1)=1-3=-2, while GD(1,2)=3-1=2. (Note that GD is anti-symmetric.)
    2. We want to find a voting (or recommendation) from each team to the others. Since the voting should be positive and bounded, one way to achieve this is by using a sigmoidal function: A = 1./(1+exp(-GD)); A(1:5:end)=0; Then we can have the voting matrix: A = 0 0.8808 0.7311 0.5000 0.1192 0 0.1192 0.1192 0.2689 0.8808 0 0.5000 0.5000 0.8808 0.5000 0 where A(i,j) is the voting from team j to team i. Note that:
      • A(i,j)=0.5 if two teams have the same number of winning games, such as A(4,1).
      • A(i,j)<0.5 if team j is stronger than team i, so team j is giving weaker vote to team i. For instance, A(2,1)<0.5 since team 1 is stronger than team 2 by 2 games.
      • A(i,j)>0.5 if team j is weaker than team i, so team j is giving stronger vote to team i. , such as A(3,2)>0.5 since team 2 is weaker than team 3 by 2 games.
    3. Next, we can convert the vote matrix A to be a transition probability matrix by dividing each column by its corresponding column sum. This can be achieved by B = bsxfun(@rdivide, A, sum(A)); Then we have the transition probability matrix B, with each column summing to 1: B = 0 0.3333 0.5414 0.4467 0.1342 0 0.0883 0.1065 0.3028 0.3333 0 0.4467 0.5630 0.3333 0.3703 0 By following the same concept as Google's PageRank, the team rank x should satisfy $Bx=x$. That is, the team rank x is an eigenvector of matrix B with corresponding eigenvalue of 1.

    By following the above reasoning steps, write a function myTeamRank.m to return the team rank, with the following usage:

    teamRank=myTeamRank(GD),
    where
    • GD: the matrix of winning game difference
    • teamRank: the returned team rank vector to show the strength of all teams
    You can download the p-file myTeamRank.p to test your function. Here is a test script with several test cases:

    Example 2: 06-線性代數/myTeamRank01.mGD=[0 2 1 0;-2 0 -2 -2;-1 2 0 0;0 2 0 0]; teamRank=myTeamRank(GD) teamRank = 0.3186 0.0998 0.2693 0.3123

    Hint:
    • Note that it is almost impossible to have an eigenvalue of exact 1 after lengthy numerical computation. Instead, you can find the eigenvalue of maximum magnitude instead.
    • In general, when using "if" statement for floating-point numbers, you need to be really careful. For instance, after lengthy computation, if you want to determine if x is equal to the square root of 2, it will be risky to write something like "if x==sqrt(2)". Instead, always try to allow some tolerance, for instance, "if abs(x-sqrt(2))<1e-5" is a better version. This will make your code more feasible and reliable.
    • Since the final team rank is a probability vector, its elements should be positive and its summation should be equal to 1.
    • More explanation on using MATLAB for team ranking can be found in this video.
MATLAB程式設計：進階篇