5-3 }x}[搎P洏

MATLAB 的 spy 指令可用於觀看稀疏矩陣的非零元素分佈情況，例如：

Example 1: 05-稀疏矩陣/spy01.mload west0479.mat % 載入二進位制檔案 west0479.mat spy(west0479) % 觀看稀疏矩陣的非零元素分佈情況

在上述這個範例中，矩陣 west0479 的維度是 479*479，但是只包含 1887 個非零元素，因此此矩陣的密度只有 1887/(479*479) = 0.0082。

此外，稀疏矩陣特別適用於表示一個「無向圖」（Undirected Graph）的「鄰近矩陣」（Adjacency Matrix）， 簡單地說，若某圖的第 i 和第 j 個節點有直線連接，則其相對應的鄰近矩陣在第 i 列、第 j 行的元素值為 1， 其他元素值則為零。以下圖為例說明：

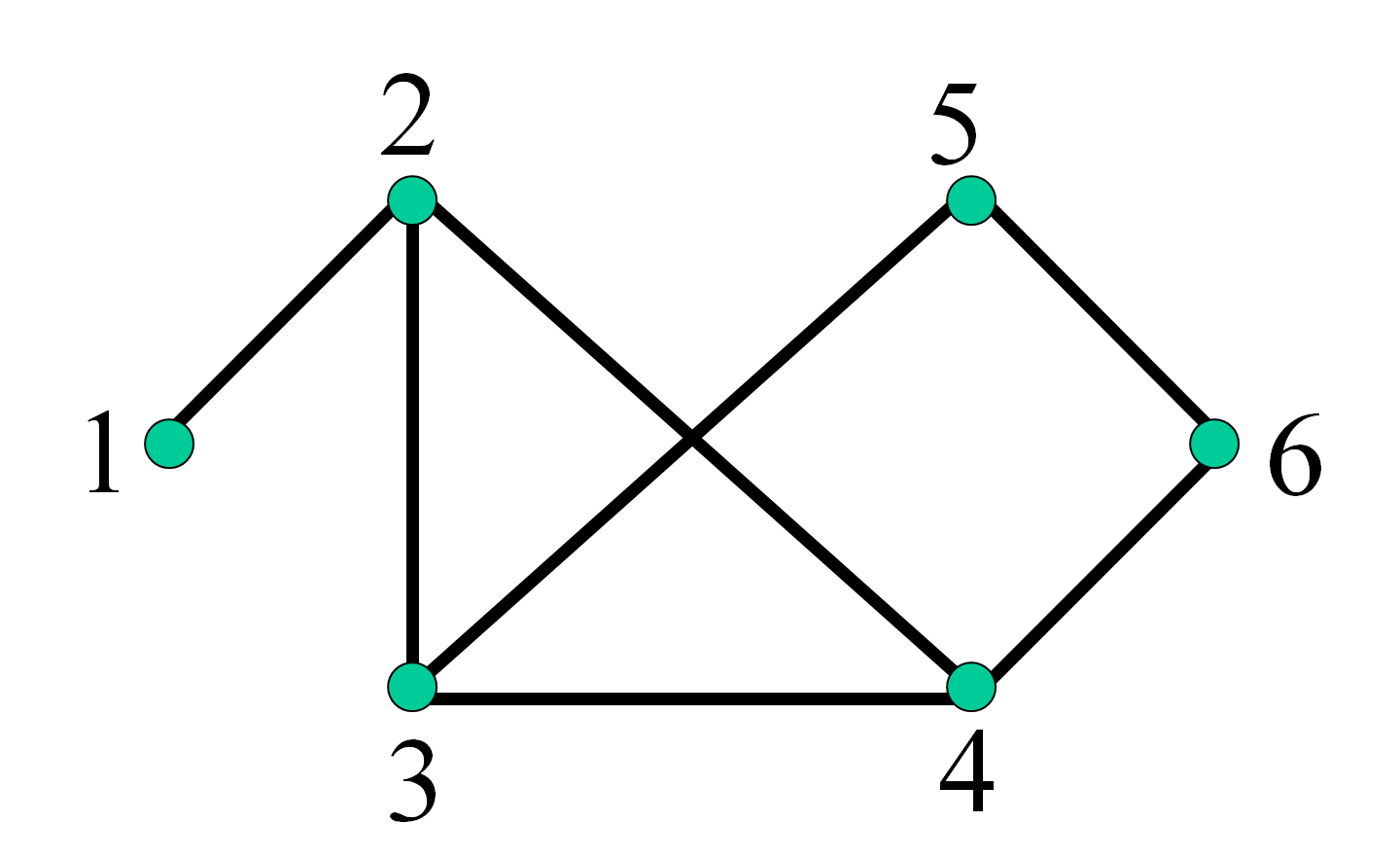
則對應的鄰近矩陣可表示成：

>> A = spconvert([1 2 1; 2 3 1; 2 4 1; 3 2 1; 3 4 1; 3 5 1; 4 2 1; 4 3 1; 4 6 1; 5 3 1; 5 6 1; 6 4 1; 6 5 1]) A = 　(1,2)　　　　1 　(3,2)　　　　1 　(4,2)　　　　1 　(2,3)　　　　1 　(4,3)　　　　1 　(5,3)　　　　1 　(2,4)　　　　1 　(3,4)　　　　1 　(6,4)　　　　1 　(3,5)　　　　1 　(6,5)　　　　1 　(4,6)　　　　1 　(5,6)　　　　1

假設這 6 個節點的座標是 (0, 1)、(1, 2)、(1, 0)、(2, 0)、(2, 2)、(3, 1)，則我們可用 gplot 指令來畫出上述的無向圖：

Example 2: 05-稀疏矩陣/gplot01.mA = spconvert([1 2 1; 2 3 1; 2 4 1; 3 4 1; 3 5 1; 5 6 1; 4 6 1]); xy = [0 1; 1 2; 1 0; 2 0; 2 2; 3 1]; % 每一個列向量是一組 (x, y) 座標 gplot(A, xy, '-o') % 畫出無向圖（Undirected Graph）

其中 '-o' 代表以實線（'-'）及圓圈（'o'）來作圖。

另一個有趣的例子是 Bucky 球，此圖包含了 60 個三度空間中的點，每一點和他的三個鄰近點都是等距離，可用 bucky 指令來產生這些點的鄰近矩陣，並用 gplot 來顯示圖形，例如：

Example 3: 05-稀疏矩陣/gplot02.m[A,xy] = bucky; % A 為鄰近矩陣，xy 為座標 gplot(A, xy, '-o'); % 畫出無向圖（Undirected Graph） axis equal % 設定 x 軸和 y 軸的刻度一樣

由上圖可看出，Bucky 球就彷彿是一個由多個五角和六角貼片所形成的足球。

另一個常用來畫出抽象圖形的指令是 treeplot，我們可用此指令來畫出一棵電腦圖學中的樹，請見下列範例：

Example 4: 05-稀疏矩陣/treePlot01.mnodes = [0 1 2 2 4 4 4 1 8 8 10 10 11 11 11 11]; treeplot(nodes)

在上述範例中，我們使用 nodes 向量來代表這一棵樹，其中 node(1)=0 則代表第一個節點是此樹的根節點（Root），而 node(i)=j 代表第 i 個節點的父親是第 j 個節點，例如 node(5)=4 代表第5個節點的父親是第 4 個節點，依此類推。讀者可以依此推論，在上述範例中的樹中，依序標出每一個節點的索引。我們也可以使用程式碼來標出每一個節點的索引，如下範例所示，你標對了嗎？

Example 5: 05-稀疏矩陣/treePlot02.mnodes = [0 1 2 2 4 4 4 1 8 8 10 10 11 11 11 11]; treeplot(nodes); h=findobj(0, 'type', 'line'); % h(1) is links; h(2) is nodes. xdata=get(h(2), 'xdata'); ydata=get(h(2), 'ydata'); for i=1:length(nodes) text(xdata(i), ydata(i), [' ', int2str(i)]); end

還有一個有趣的例子，是由 NASA （美國太空總署）所主導的計畫，其中包含計算流過機翼的氣流所造成的作用力，由於必須進行偏微分方程的數值運算，所以必須對二維空間進行三角化切割，其鄰近矩陣即為一個稀疏矩陣，您可在 MATLAB 下執行 showdemo airfoil.m 指令即可產生相關圖形及說明，在此不再贅述。

MATLAB程式設計：進階篇