一般而言,曲線擬合(Curve Fitting)所建立的數學模型是「單輸入、單輸出」(Single-input Single-output,簡稱SISO),所以其特性可用一條曲線來表示。若欲建立具有兩個輸入的數學模型,則其特性可用一個曲面來表示,此類問題可稱為曲面擬合(Surface Fitting)。相同的概念,可以延伸到一般的「多輸入、單輸出」(MISO) 或「多輸入、多輸出」(MIMO)的數學模型,例如類神經網路(Artificial Neural Networks)等。
無論是曲線擬合或是曲面擬合(或是其它多輸入模型的擬合問題),在資料分析上都稱為迴歸分析(Regression Analysis),或稱為資料擬合(Data Fitting),其牽涉到的數學理論與分析技巧相當廣泛。但在本章中,我們只介紹幾種最基本的方法,以及如何使用 MATLAB 來實現這些基本的方法。
迴歸分析與所使用的數學模型有很大的關係,如果所使用的模型是線性模型,則此類問題稱為線性迴歸(Linear Regression);反之,若使用非線性模型,則稱為非線性迴歸(Nonlinear Regression)。本節將介紹線性迴歸,下節則介紹非線性迴線。
線性迴歸是在迴歸分析中最常用的方法,其標準解法及相關數學性質可見於一般統計或資料分析的教科書,因此本章不針對理論及數學推導詳述,讀者可自行參考相關書籍。以下將以簡單範例來說明如何使用 MATLAB 來進行線性迴歸。
假設我們的觀察資料是美國自 1790 至 1990 年(以 10 年為一單位)的總人口,此資料可由載入檔案 census.mat 得到,如下:
其中 cdate 為年度,pop 為人口總數,兩者都是長度為 21 的向量。假設我們要預測在西元 2000 年及 2010 年的美國人口總數,我們就必須根據上述資料來建立一數學模型,並依此模型來進行預測。
由上圖資料點走勢,我們可以觀察得知,通過這些點的曲線可能是一條二次的拋物線,所以我們可以假設所需的數學模型為 $$ y = f(x; a_0, a_1, a_2) = a_0+a_1x+a_2x^2 $$
其中 $y$(人口總數)為此模型的輸出,$x$(年度)為此模型的輸入,$[a_0,a_1, a_2]$ 則為此模型的參數(Parameters)。由於這些參數相對於輸出 y 是呈線性關係,所以此模型稱為「具有線性參數(Linear-in-the-parameters)」的模型,我們的任務則是找出最好的參數值,使得模型輸出與實際資料越接近越好,此過程即稱為線性迴歸(Linear Regression)。
假設我們的觀察資料可寫成 $(x_i, y_i), i = 1 - 21$。當輸入為 $x_i$ 時,實際輸出為 $y_i$,但模型的預測值為 $f(x_i; a_0, a_1, a_2) = a_0+a_1x_i+a_2x_i^2$,因此平方誤差為 $[y_i-f(x_i)]^2$,而總平方誤差 則可表示如下: $$ E(a_0, a_1, a_2) = \sum_{i=1}^{21}[y_i-f(x_i)]^2 = \sum_{i=1}^{21}[y_i-(a_0+a_1x_i+a_2x_i^2)]^2 $$
上述平方誤差 $E$ 是參數 $a_0$、$a_1$、$a_2$ 的函數,因此由基本微積分得知,若要求得 $E$ 的最小值,我們可以求出 $E$ 對 $a_0$、$a_1$、$a_2$ 的導式,令其為零,即可解出 $a_0$、$a_1$、$a_2$ 的最佳值。更進一步觀察,我們知道此模型具線性參數,所以平方誤差 $E$ 為 $a_0$、$a_1$、$a_2$ 的二次式,而導式 $\frac{\partial E}{\partial a_0}$、$\frac{\partial E}{\partial a_1}$ 及 $\frac{\partial E}{\partial a_2}$ 為 $a_0$、$a_1$、$a_2$的一次式,因此在令導式為零之後,我們可以得到一組三元一次線性聯立方程式,就可以解出參數 $a_0$、$a_1$、$a_2$ 的最佳值。
從另一方面來看,假設 21 個觀察點均通過此拋物線,則我們可以將這 21 個點帶入此拋物線方程式,得到下列 21 個等式:
$$ \left\{ \begin{matrix} a_0 + a_1 x_1 + a_2 x_1^2 & = & y_1\\ a_0 + a_1 x_2 + a_2 x_2^2 & = & y_1\\ \vdots & = & \vdots \\ a_0 + a_1 x_{21} + a_2 x_{21}^2 & = & y_{21}\\ \end{matrix} \right. $$亦可寫成
$$ \underbrace{ \left[ \begin{matrix} 1 & x_1 & x_1^2\\ 1 & x_2 & x_2^2\\ \vdots & \vdots & \vdots\\ 1 & x_{21} & x_{21}^2\\ \end{matrix} \right] }_A \underbrace{ \left[ \begin{matrix} a_1\\ a_2\\ a_3\\ \end{matrix} \right] }_\theta = \underbrace{ \left[ \begin{matrix} y_1\\ y_2\\ \vdots\\ y_{21}\\ \end{matrix} \right] }_y $$其中 $A$、$y$ 為已知,$\theta$ 為未知向量。很明顯的,上述方程組含 21 個方程式,但卻只有 3 個未知數 $\theta=\left[\theta_1, \theta_2, \theta_3 \right]^T$,所以通常不存在一組解來滿足這 21 個方程式。在一般情況下,我們只能找到一組 $\theta$,使得等號兩邊的差異為最小,此差異可寫成
$$ \left\| y-A\theta \right\|^2 = (y-A\theta)^T(y-A\theta) $$此即為前述的總平方誤差 $E$。
由於此類問題在線性迴歸經常碰到,所以 MATLAB 提供一個簡單方便的「左除」(\)指令,來解出最佳的 $\theta$。(我們在本章最後一小節會說明如何以矩陣的操作來算出 $\theta$ 的最佳值。)在以下範例中,我們利用「左除」來算出最佳的 $\theta$ 值,並同時畫出具有最小平方誤差的二次曲線,如下:
由上述範例,我們可以找出最佳的 $\theta=[a_0, a_1, a_2]=[21130, 23.51, 0.00654]$,因此具有最小平方誤差的拋物線可以寫成: $$ y = f(x) = a_0 + a_1 x + a_2 x^2 = 21130 + 23.51 x + 0.00654 x^2 $$
根據圖形,此方程式已經能夠相當逼近所給的 21 個觀察點。根據此拋物線數學模型,我們可以預測美國在 2000 和 2010 年的人口總數為:
在上述例子中,我們的數學模型是一個二次拋物線,我們可將之推廣,得到一個 n 次多項式:
$$y = f(x) = a_0 + a_1 x + a_2 x^2 + \cdots + a_n x^n$$利用多項式的數學模型來進行曲線擬合,通稱為「多項式擬合(Polynomial Fitting)」,也是在資料分析常用到的技巧。針對多項式擬合,MATLAB 提供了 polyfit 指令來找出最佳參數,其效果和「左除」(\)是一致的。一旦找出最佳參數後,我們可以使用 polyval 指令來計算多項式的值,程式碼更加簡潔,請見下列範例:
在上述範例中,「polyfit(cdate, pop, 2)」中的 2 代表我們用到的模型是 2 次多項式。使用 polyfit 和 polyval,是不是讓程式碼簡短很多呢?有關 polyfit、polyval 及其它相關的多項式指令,可見本書「多項式的處理及分析」章節。
線性迴歸的成功與否,與所選取的模型有很大的關係。模型所含的參數越多,平方誤差會越小,若參數個數等於資料點個數,則在一般情況下,平方誤差會等於零,但這並不表示預測會最準,因為資料點含有雜訊,完全吻合資料的模型亦代表此模型受雜訊的影響最大,預測之準確度也會較差。因此,「模型複雜度」(即可變參數的個數)和「預測準確度」是相互抗衡的兩個因素,無法兩者兼得,因此我們必須經由對問題本身的瞭解,來找到一個平衡點。
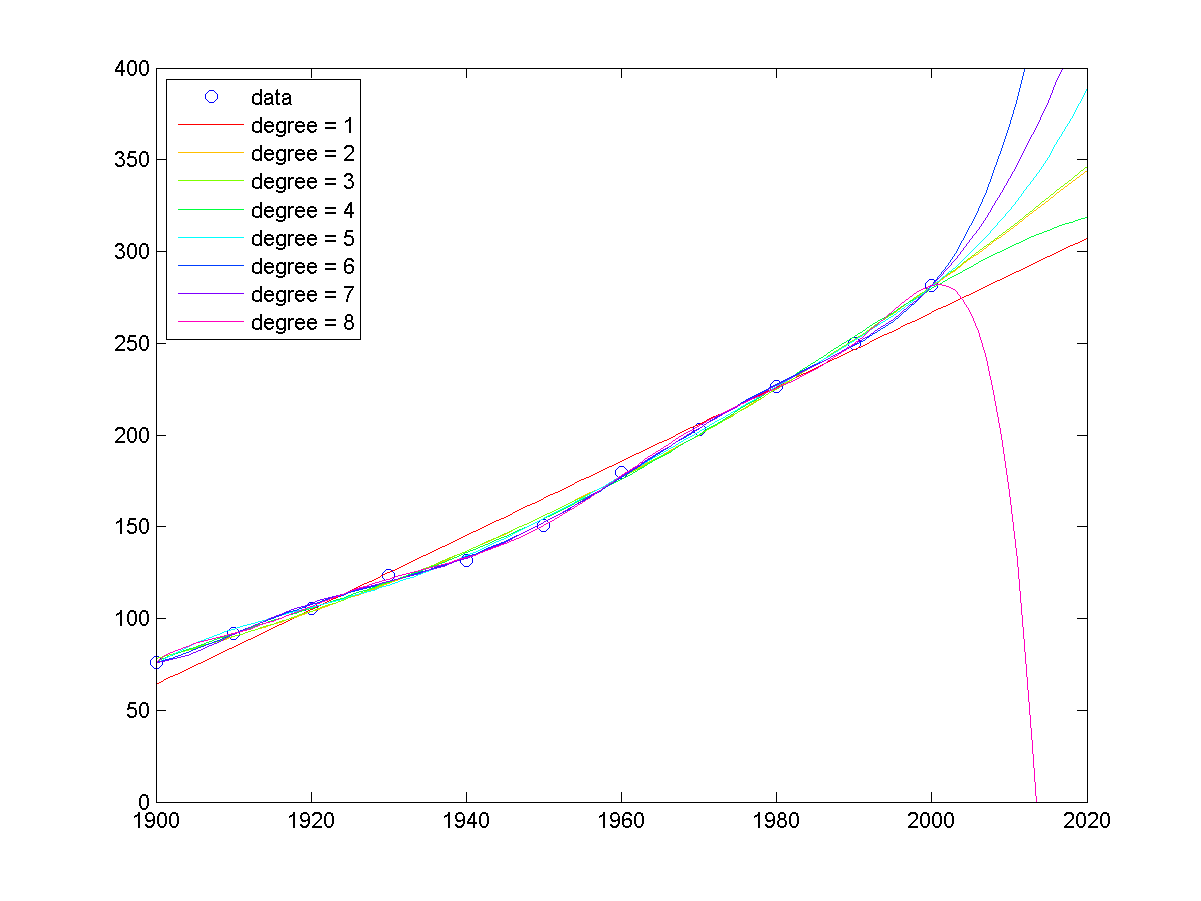
若在 MATLAB 下輸入「census」,就可以看到使用不同次數的多項式,來對 census 資料進行曲線擬合的結果,如下:
由上述圖形可以看出,當多項式的次數越來越高時,「外插」常會出現不可信的結果。例如在上圖中,使用 degree=8 的曲線來預測 2020 年的人口,反而出現不升反降的情況(難道是發生了世界大戰?),這種反常的結果,表示我們選用的模型參數太高,雖然誤差的平方和變小了,但是預測的可靠度也下降了。
MATLAB程式設計:進階篇