�@��Ө��A���u���X�]Curve Fitting�^�ҫإߪ��ƾǼҫ��O�u���J�B���X�v�]Single-input Single-output�A²��SISO�^�A�ҥH��S�ʥi�Τ@�����u�Ӫ��ܡC�Y���إߨ㦳��ӿ�J���ƾǼҫ��A�h��S�ʥi�Τ@�Ӧ����Ӫ��ܡA�������D�i�٬��������X�]Surface Fitting�^�C�ۦP�������A�i�H������@�몺�u�h��J�B���X�v�]MISO�^ �Ρu�h��J�B�h��X�v�]MIMO�^���ƾǼҫ��A�Ҧp�����g�����]Artificial Neural Networks�^���C
�L�O���u���X�άO�������X�]�άO�䥦�h��J�ҫ������X���D�^�A�b��Ƥ��R�W���٬��j�k���R�]Regression Analysis�^�A�κ٬�������X�]Data Fitting�^�A��o�A�쪺�ƾDzz�P���R�ޥ��۷��s�x�C���b�������A�ڭ̥u���дX�س̰���k�A�H�Φp��ϥ� MATLAB �ӹ�{�o�ǰ���k�C
�j�k���R�P�ҨϥΪ��ƾǼҫ����ܤj�����Y�A�p�G�ҨϥΪ��ҫ��O�u�ʼҫ��A�h�������D�٬��u�ʰj�k�]Linear Regression�^�F�Ϥ��A�Y�ϥΫD�u�ʼҫ��A�h�٬��D�u�ʰj�k�]Nonlinear Regression�^�C���`�N���нu�ʰj�k�A�U�`�h���ЫD�u�ʰj�u�C
�u�ʰj�k�O�b�j�k���R���̱`�Ϊ���k�A��зǸѪk�ά����ƾǩʽ�i����@��έp�θ�Ƥ��R���Ь�ѡA�]���������w��z�פμƾDZ��ɸԭz�AŪ�̥i�ۦ�ѦҬ������y�C�H�U�N�H²��d�Ҩӻ����p��ϥ� MATLAB �Ӷi��u�ʰj�k�C
���]�ڭ̪��[���ƬO����� 1790 �� 1990 �~�]�H 10 �~���@���^���`�H�f�A����ƥi�Ѹ��J�ɮ� census.mat �o��A�p�U�G
�䤤 cdate ���~�סApop ���H�f�`�ơA��̳��O���� 21 ���V�q�C���]�ڭ̭n�w���b�褸 2000 �~�� 2010 �~������H�f�`�ơA�ڭ̴N�����ھڤW�z��ƨӫإߤ@�ƾǼҫ��A�è̦��ҫ��Ӷi��w���C
�ѤW�ϸ���I���աA�ڭ̥i�H�[��o���A�q�L�o���I�����u�i��O�@���G�����ߪ��u�A�ҥH�ڭ̥i�H���]�һݪ��ƾǼҫ��� $$ y = f(x; a_0, a_1, a_2) = a_0+a_1x+a_2x^2 $$
�䤤 $y$�]�H�f�`�ơ^�����ҫ�����X�A$x$�]�~�ס^�����ҫ�����J�A$[a_0,a_1, a_2]$ �h�����ҫ����Ѽơ]Parameters�^�C�ѩ�o�ǰѼƬ۹���X y �O�e�u�����Y�A�ҥH���ҫ��٬��u�㦳�u�ʰѼơ]Linear-in-the-parameters�^�v���ҫ��A�ڭ̪����ȫh�O��X�̦n���ѼƭȡA�ϱo�ҫ���X�P��ڸ�ƶV����V�n�A���L�{�Y�٬��u�ʰj�k�]Linear Regression�^�C
���]�ڭ̪��[���ƥi�g�� $(x_i, y_i), i = 1 - 21$�C����J�� $x_i$ �ɡA��ڿ�X�� $y_i$�A���ҫ����w���Ȭ� $f(x_i; a_0, a_1, a_2) = a_0+a_1x_i+a_2x_i^2$�A�]������~�t�� $[y_i-f(x_i)]^2$�A���`����~�t �h�i���ܦp�U�G $$ E(a_0, a_1, a_2) = \sum_{i=1}^{21}[y_i-f(x_i)]^2 = \sum_{i=1}^{21}[y_i-(a_0+a_1x_i+a_2x_i^2)]^2 $$
�W�z����~�t $E$ �O�Ѽ� $a_0$�B$a_1$�B$a_2$ ����ơA�]���ѰL�n���o���A�Y�n�D�o $E$ ���̤p�ȡA�ڭ̥i�H�D�X $E$ �� $a_0$�B$a_1$�B$a_2$ ���ɦ��A�O�䬰�s�A�Y�i�ѥX $a_0$�B$a_1$�B$a_2$ ���̨έȡC��i�@�B�[��A�ڭ̪��D���ҫ���u�ʰѼơA�ҥH����~�t $E$ �� $a_0$�B$a_1$�B$a_2$ ���G�����A�Ӿɦ� $\frac{\partial E}{\partial a_0}$�B$\frac{\partial E}{\partial a_1}$ �� $\frac{\partial E}{\partial a_2}$ �� $a_0$�B$a_1$�B$a_2$���@�����A�]���b�O�ɦ����s����A�ڭ̥i�H�o��@�դT���@���u���p�ߤ�{���A�N�i�H�ѥX�Ѽ� $a_0$�B$a_1$�B$a_2$ ���̨έȡC
�q�t�@�譱�ӬݡA���] 21 ���[���I���q�L���ߪ��u�A�h�ڭ̥i�H�N�o 21 ���I�a�J���ߪ��u��{���A�o��U�C 21 �ӵ����G
$$ \left\{ \begin{matrix} a_0 + a_1 x_1 + a_2 x_1^2 & = & y_1\\ a_0 + a_1 x_2 + a_2 x_2^2 & = & y_1\\ \vdots & = & \vdots \\ a_0 + a_1 x_{21} + a_2 x_{21}^2 & = & y_{21}\\ \end{matrix} \right. $$��i�g��
$$ \underbrace{ \left[ \begin{matrix} 1 & x_1 & x_1^2\\ 1 & x_2 & x_2^2\\ \vdots & \vdots & \vdots\\ 1 & x_{21} & x_{21}^2\\ \end{matrix} \right] }_A \underbrace{ \left[ \begin{matrix} a_1\\ a_2\\ a_3\\ \end{matrix} \right] }_\theta = \underbrace{ \left[ \begin{matrix} y_1\\ y_2\\ \vdots\\ y_{21}\\ \end{matrix} \right] }_y $$�䤤 $A$�B$y$ ���w���A$\theta$ �������V�q�C�ܩ��㪺�A�W�z��{�էt 21 �Ӥ�{���A���o�u�� 3 �ӥ����� $\theta=\left[\theta_1, \theta_2, \theta_3 \right]^T$�A�ҥH�q�`���s�b�@�ոѨӺ����o 21 �Ӥ�{���C�b�@�뱡�p�U�A�ڭ̥u����@�� $\theta$�A�ϱo�������䪺�t�����̤p�A���t���i�g��
$$ \left\| y-A\theta \right\|^2 = (y-A\theta)^T(y-A\theta) $$���Y���e�z���`����~�t $E$�C
�ѩ������D�b�u�ʰj�k�g�`�I��A�ҥH MATLAB ���Ѥ@��²���K���u�����v�]\�^���O�A�ӸѥX�̨Ϊ� $\theta$�C�]�ڭ̦b�����̫�@�p�`�|�����p��H�x�}���ާ@�Ӻ�X $\theta$ ���̨έȡC�^�b�H�U�d�Ҥ��A�ڭ̧Q�Ρu�����v�Ӻ�X�̨Ϊ� $\theta$ �ȡA�æP�ɵe�X�㦳�̤p����~�t���G�����u�A�p�U�G
�ѤW�z�d�ҡA�ڭ̥i�H��X�̨Ϊ� $\theta=[a_0, a_1, a_2]=[21130, 23.51, 0.00654]$�A�]���㦳�̤p����~�t���ߪ��u�i�H�g���G $$ y = f(x) = a_0 + a_1 x + a_2 x^2 = 21130 + 23.51 x + 0.00654 x^2 $$
�ھڹϧΡA����{���w�g����۷��G��ҵ��� 21 ���[���I�C�ھڦ��ߪ��u�ƾǼҫ��A�ڭ̥i�H�w������b 2000 �M 2010 �~���H�f�`�Ƭ��G
�b�W�z�Ҥl���A�ڭ̪��ƾǼҫ��O�@�ӤG���ߪ��u�A�ڭ̥i�N�����s�A�o��@�� n ���h�����G
$$y = f(x) = a_0 + a_1 x + a_2 x^2 + \cdots + a_n x^n$$�Q�Φh�������ƾǼҫ��Ӷi�榱�u���X�A�q�٬��u�h�������X�]Polynomial Fitting�^�v�A�]�O�b��Ƥ��R�`�Ψ쪺�ޥ��C�w��h�������X�AMATLAB ���ѤF polyfit ���O�ӧ�X�̨ΰѼơA��ĪG�M�u�����v�]\�^�O�@�P���C�@����X�̨ΰѼƫ�A�ڭ̥i�H�ϥ� polyval ���O�ӭp��h�������ȡA�{���X��[²��A�Ш��U�C�d�ҡG
�b�W�z�d�Ҥ��A�upolyfit(cdate, pop, 2)�v���� 2 �N���ڭ̥Ψ쪺�ҫ��O 2 ���h�����C�ϥ� polyfit �M polyval�A�O���O���{���X²�u�ܦh�O�H���� polyfit�Bpolyval �Ψ䥦�������h�������O�A�i�����ѡu�h�������B�z�Τ��R�v���`�C
�u�ʰj�k�����\�P�_�A�P�ҿ�����ҫ����ܤj�����Y�C�ҫ��ҧt���ѼƶV�h�A����~�t�|�V�p�A�Y�ѼƭӼƵ������I�ӼơA�h�b�@�뱡�p�U�A����~�t�|����s�A���o�ä����ܹw���|�̷ǡA�]������I�t�����T�A�����k�X��ƪ��ҫ���N�����ҫ������T���v�T�̤j�A�w�����ǽT�פ]�|���t�C�]���A�u�ҫ������סv�]�Y�i�ܰѼƪ��Ӽơ^�M�u�w���ǽT�סv�O�ۤ��ܿŪ���Ӧ]���A�L�k��̭ݱo�A�]���ڭ̥����g�ѹ���D�������A�ѡA�ӧ��@�ӥ����I�C
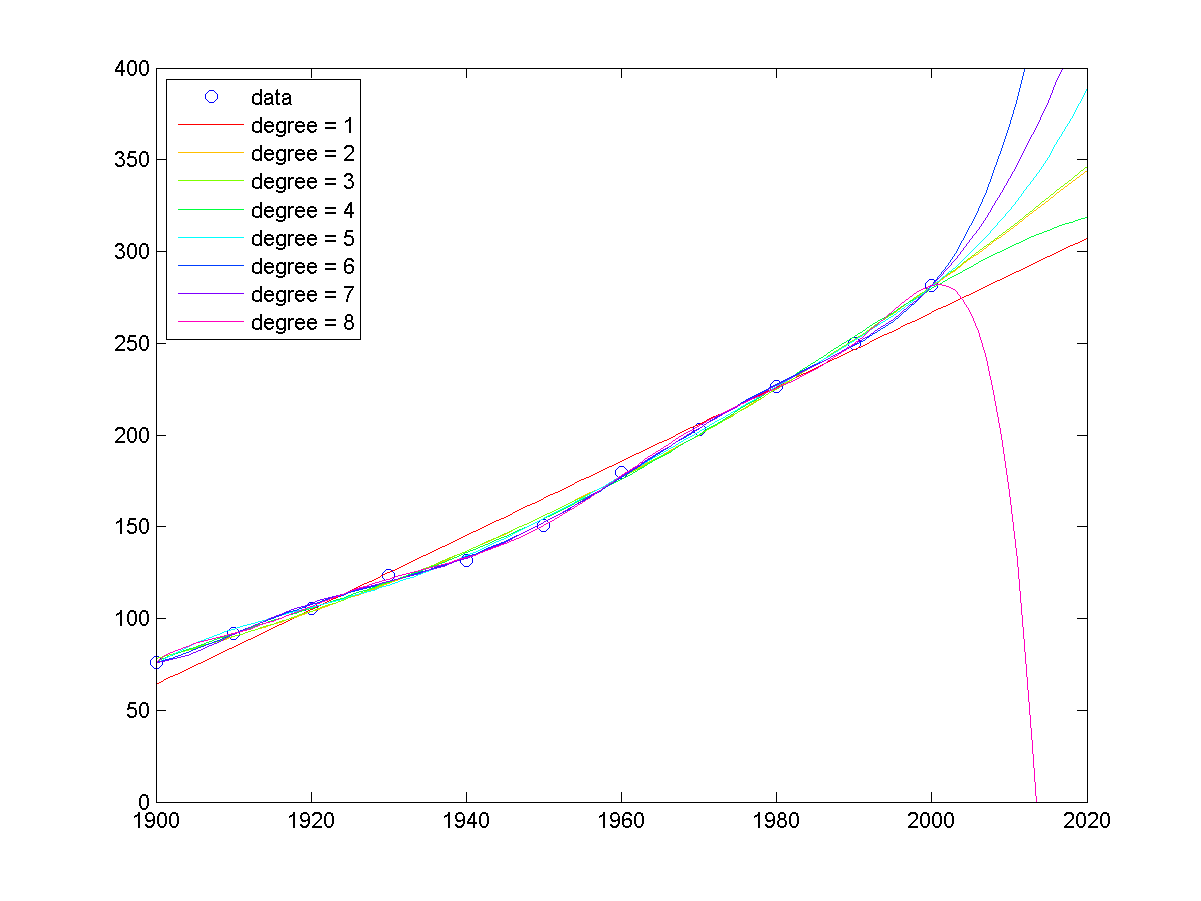
�Y�b MATLAB �U��J�ucensus�v�A�N�i�H�ݨ�ϥΤ��P���ƪ��h�����A�ӹ� census ��ƶi�榱�u���X�����G�A�p�U�G
�ѤW�z�ϧΥi�H�ݥX�A���h���������ƶV�ӶV���ɡA�u�~���v�`�|�X�{���i�H�����G�C�Ҧp�b�W�Ϥ��A�ϥ� degree=8 �����u�ӹw�� 2020 �~���H�f�A�ϦӥX�{���ɤϭ������p�]���D�O�o�ͤF�@�ɤj�ԡH�^�A�o�ؤϱ`�����G�A���ܧڭ̿�Ϊ��ҫ��ѼƤӰ��A���M�~�t������M�ܤp�F�A���O�w�����i�a�פ]�U���F�C
MATLAB�{���]�p�G�i���g