所謂「一維內插」(1-D Interpolation),就是根據一組已知的資料點(包含輸入及輸出,其中輸入是一維資料,輸出也是一維資料),來建立一個連續的函數,以便計算任意輸入資料點所對應的輸出值。一維內插的方法很多,MATLAB 提供了兩種基本方法:
- 基於多項式的內插法
- 基於FFT(Fast Fourier Transform,快速傅立葉轉換)的內插法
本節將對這兩種方法來進行說明。
MATLAB 最常用的一維內插指令是 interp1,其原理是利用多項式來進行內插運算。interp1 的使用語法為
yi = interp1(x, y, xi, method)
其中向量 x 是資料點的 x 座標(輸入值),向量 y 是資料點的 y 座標(輸出值),向量 xi 是內插點(輸入值,未知其對應輸出值),字串 method 則指定使用的內插方法,共有六種:
- 'nearest':鄰近點內插法
- 'linear':線性內插法
- 'spline':片段式的三次 Spline 內插法
- 'pchip':保持形狀的片段式三次內插
- 'cubic':和'pchip' 一樣
- 'v5cubic':MATLAB 5 所用的三次內插法
在下列範例中,我們使用上述方法中的前四種來對一維資料進行內插:
由上圖可看出,Spline 和 Cubic 所產生的曲線較平滑,但它們所需的計算時間也較久。以上這四種內插法的比較表如下:
| |
Nearest |
Linear |
Cubic |
Cubic Spline |
| 執行時間
| 1(短) |
2 |
3 |
4(長) |
| 曲線平滑度
| 1(差) |
2 |
3 |
4(好) |
| 記憶體使用量
| 1(少) |
2 |
4(多) |
3 |
在使用 interp1 時,向量 x 必須是嚴格遞增或遞減,但元素之間不必是等間隔。此外,xi 的範圍也必須落在 x 的範圍之內,才能進行內插的運算。
在上述範例的圖形,可能不容易看出每一種方法的效果,筆者特別另外寫了一個程式,可以讓使用者拖放取樣點,內插曲線就會跟著改變,檔案名稱是 interpAnim01.m,執行後的圖形如下:
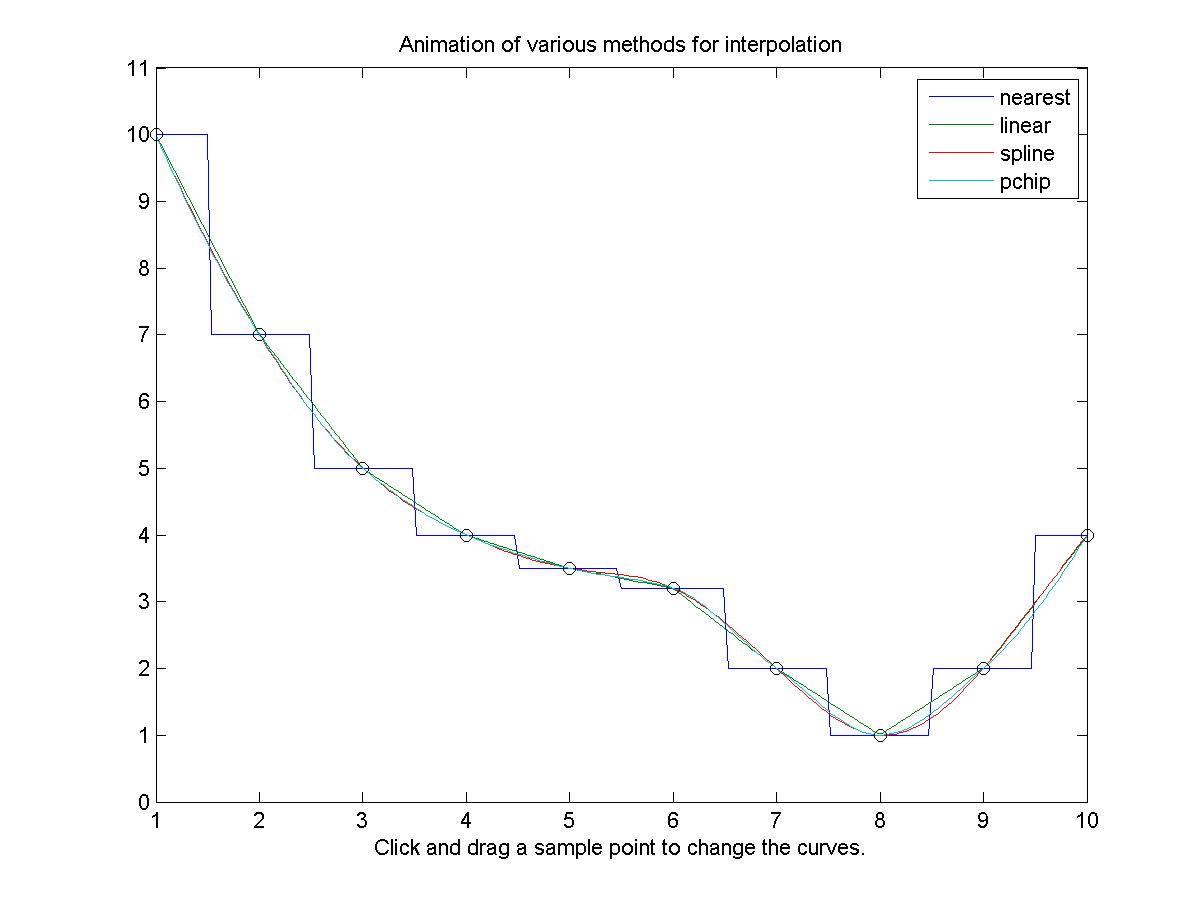
使用者可以在上述圖形視窗中,拖放每一個取樣點,就可以立刻看到內插曲線的變化,也同時可以知道各種內插方法的特性。
除了 interp1 之外,另一個較少用的 MATLAB 的指令 interpft 可進行基於 FFT(Fast Fourier Transform,快速傅立葉轉換)的內插法。此方法先計算資料點的傅立葉轉換,再用更密集的內插點來進行反傅立葉轉換。interft 的使用語法為
y = interpft(yi, n)
其中向量 yi 是一個經由等距取點的函數值,n 則是等距取點的內插點數。例如:
如果我們要根據平面上的有限資料點,來描繪初一個物體的外型,也可以使用一維內插,但是此時內插資料點會變成兩組,分別是
- X座標對其索引(Index,或稱指標)的內插
- Y座標對其索引(Index,或稱指標)的內插
在下列範例中,我們共有七個資料點,散佈在二度空間,我們可以使用 interp1 的 spline 方法,來畫出連續平滑的圖形,如下:
在上述範例中,原有的資料只有七點,但是使用一維內插,我們就可以產生平滑連續的圖形,這也是在電腦圖學(Computer Graphics)最常見的做法,也就是以少數控制點(Control Points)來代表一個物件,然後再使用內插來產生整個物件的細緻圖形。
當然,如果我們選用不同的方法,得到的平滑效果也會不同,下列範例使用 interp1 的四種方法,來對上一個範例的資料點進行內插,如下:
同樣地,在上述範例的圖形,可能不容易看出每一種方法的效果,筆者特別另外寫了一個程式,可以讓使用者拖放取樣點,內插曲線就會跟著改變,檔案名稱是 interpAnim02.m,執行後的圖形如下:
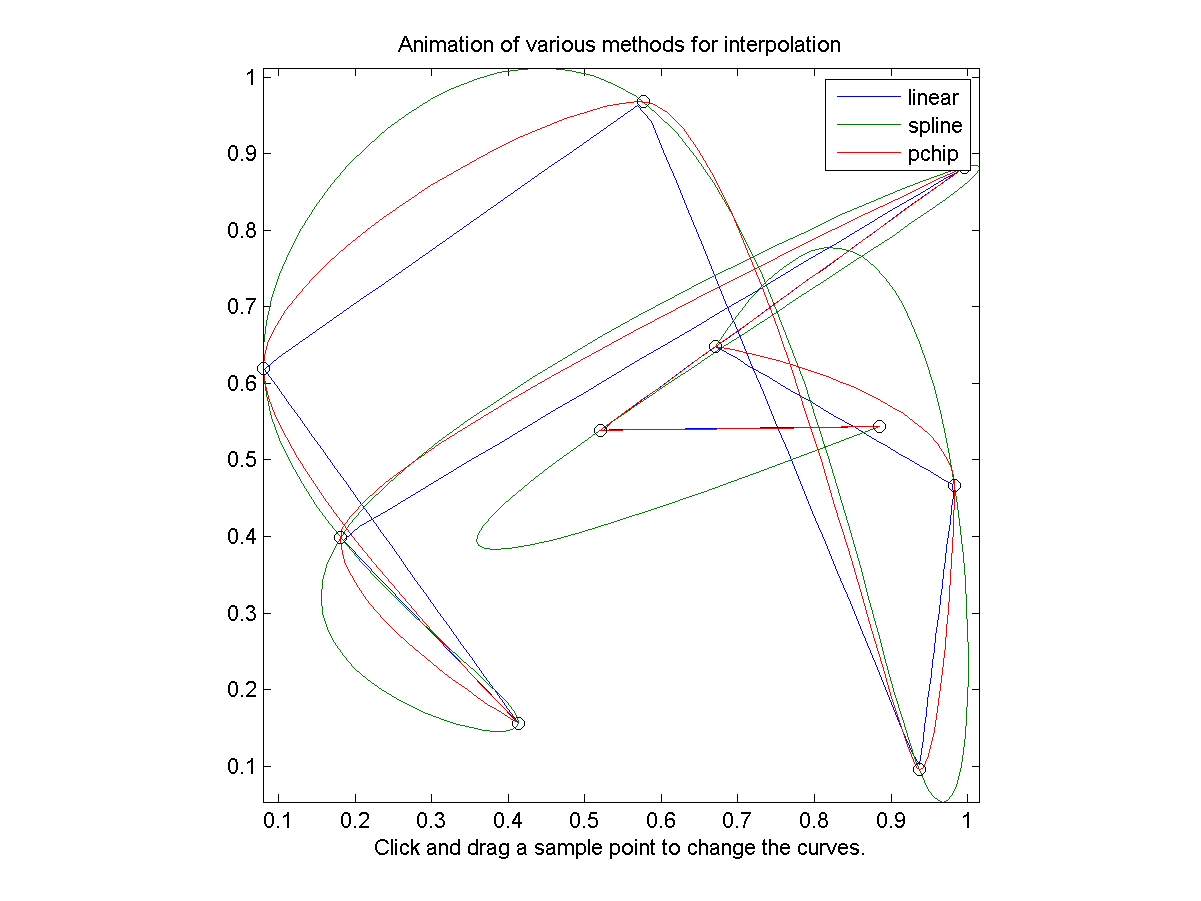
這個展示程式很有趣,請讀者務必自己試看看,拖放幾個控制點,看看會產生什麼不同效果的內插曲線。
MATLAB程式設計:進階篇



