- 下列聯立方程式有無窮多組交點:
$$
\left\{
\begin{array}{l}
y = 1/x\\
y = sin(x)
\end{array}
\right.
$$
- 假設這些交點可以表示成 $(x_1, y_1), (x_2, y_2), (x_3, y_3), \cdots$, 而且 $x_1 < x_2 < x_3 < \cdots$。請用 fzero 指令,找出 $x_1, x_2, x_3$。
- 請畫出代表上述兩個方程式的曲線,並用小圓圈標示出 $(x_1, y_1), (x_2, y_2), (x_3, y_3)$ 的位置,以驗證你在前一小題的答案。
- Find a point to minimize distance difference:
Given two set of points A and B on a 2D space, find a point (x,0) on the X-axis such that the sum of distance to all points in A is equal to to sum of distance to all points in B. In other words, you need to write a function equalDistance.m with the following usage:
x = equalDistance(A, B); where- A is a matrix of 2 by m, representing m points in a 2D plane
- B is a matrix of 2 by n, representing n points in a 2D plane
- x is the returned output
Here is a test example:
- Find a line to minimize distance difference:
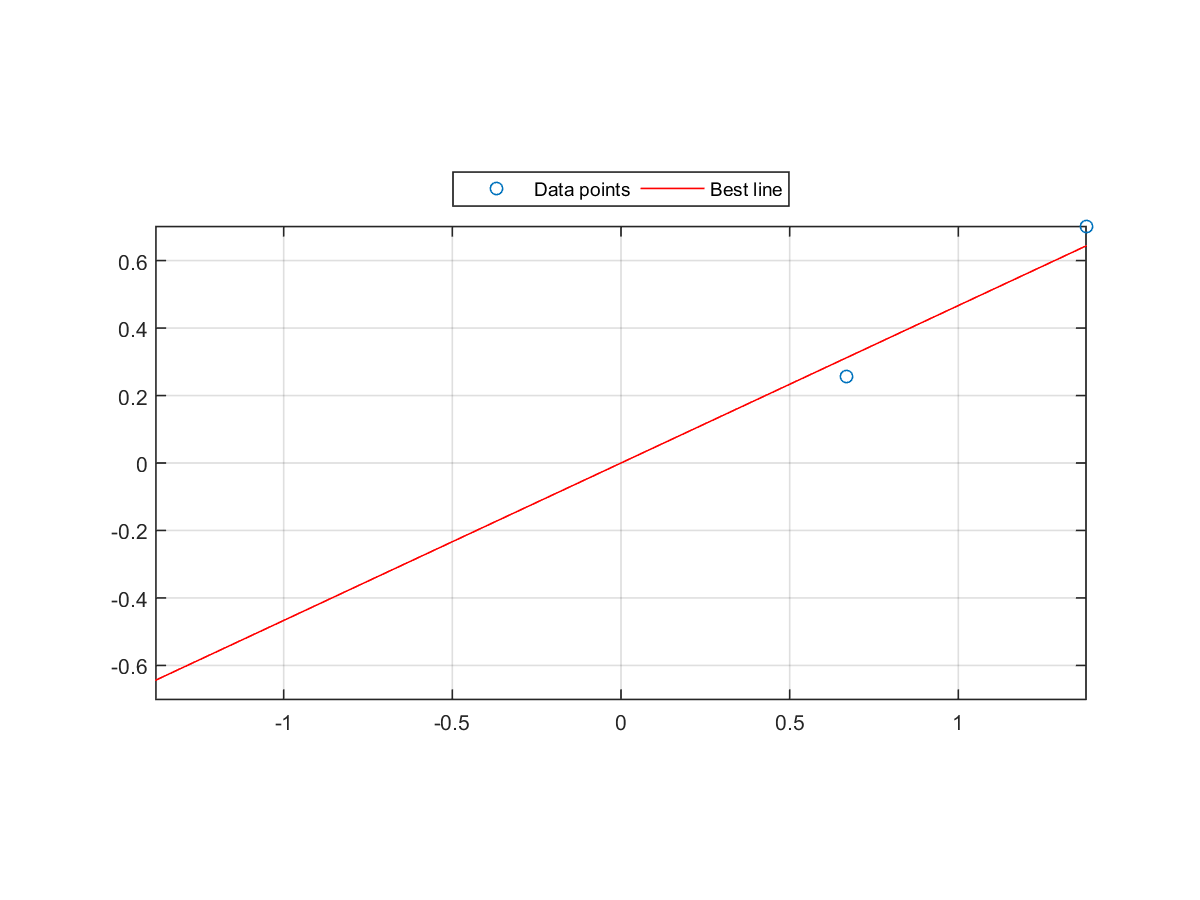
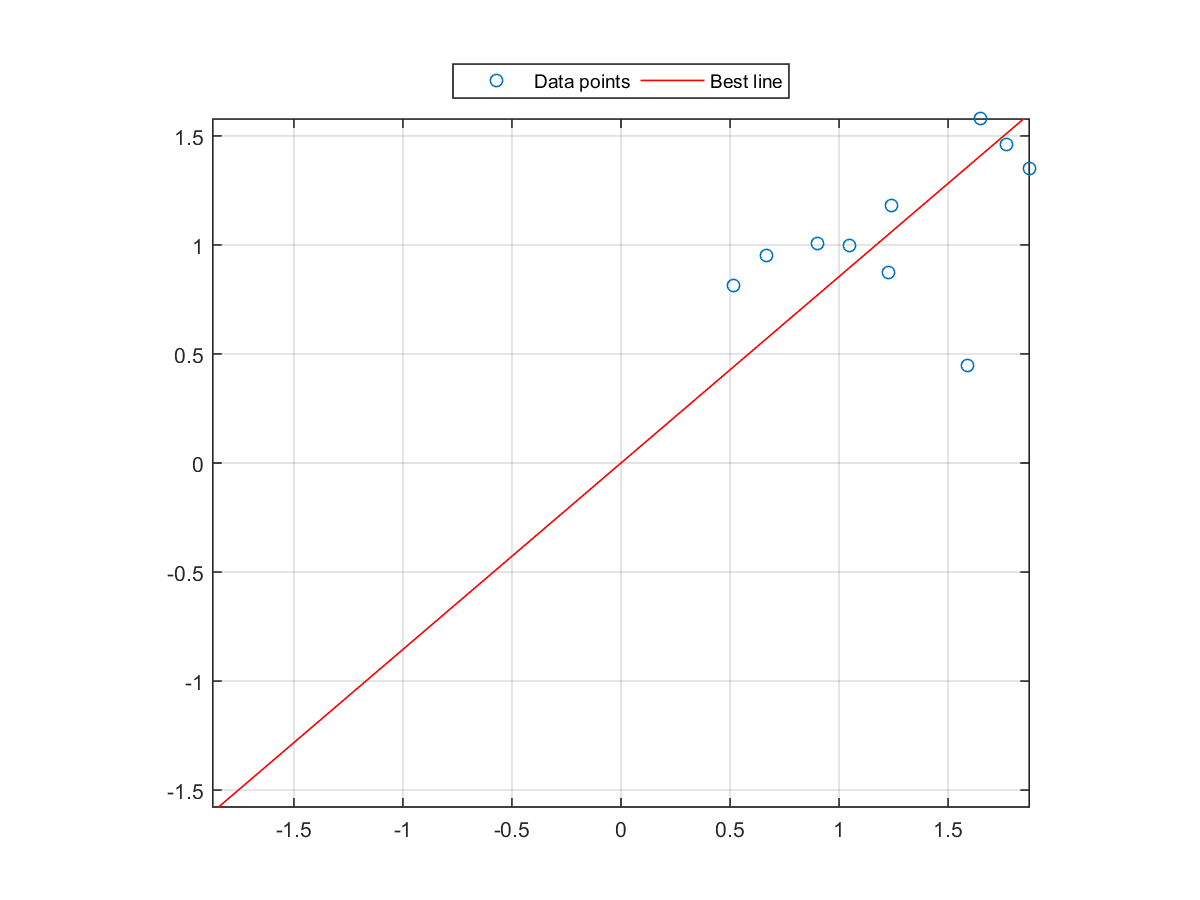
Given a set of points A on a 2D space, find a line y=alpha*x such that the sum of distance to all points above the line is equal to to sum of distance to all points below the line. In other words, you need to write a function equalDistanceFromLine.m with the following usage:
alpha = equalDistanceFromLine(A); where- A is a matrix of 2 by m, representing m points in a 2D plane
- alpha is the slope of the separating line
Test cases
- A = [0.669615828536535 1.37831002494;0.255156313573849 0.700802957390634] ==> alpha = 0.46679388774826
- A = [1.0459613413713 1.64836240385754 0.668148281107254 1.24009361110736 1.76736994372824 0.514183249250956 1.22696476792286 1.87222221905272 1.58712322506665 0.899136620392806;0.995918733217741 1.57784235228208 0.949856035477784 1.1820334094137 1.46127638101438 0.816264168546478 0.872065204595773 1.35287364461043 0.445267025957944 1.00539440958911] ==> alpha = 0.854784493132274
- 在 XY 平面上給定三點 A、B、C,找出另外一點 X,使得 X 到 A、B、C 三點的距離和為最小。請寫一個函式 mindist.m 解決上述問題,此函式的輸出入格式如下:
x = mindist(a, b, c) 其中 a、b、c 為三點的座標,x 則是輸出點的座標,你必須使用 fminsearch 指令來進行最佳化。- 當 a = [4 0]、b = [0 3]、c = [0 0] 時,mindist.m 所傳回的 x 值為何?對應的最短距離和為何?
- 在上小題中,當最短距離和發生時,角度 $\angle AXB$、$\angle BXC$、$\angle CXA$ 各是多少?
- 在 XY 平面上給定三點 A、B、C,找出另外一點 X,使得 X 到 A、B、C 三點的距離平方和為最小。請寫一個函式 mindist2.m 解決上述問題,此函式的輸出入格式如下:
x = mindist2(a, b, c) 其中 a、b、c 為三點的座標,x 則是輸出點的座標,你必須使用 fminsearch 指令來進行最佳化。- 當 a = [4 0]、b = [0 3]、c = [0 0] 時,mindist2.m 所傳回的 x 值為何?對應的最短距離平方和為何?
- 在上小題中,當最短距離平方和發生時,x-(a+b+c)/3 的長度是多少?
- 在 XY 平面上給定一組行向量 x1, x2, ... xn,請找出一個單位向量 u,使得這一組向量在 u 方向的投影量平方和為最小。請寫一個函式 minProj.m 解決上述問題,此函式的輸出入格式如下:
u = minproj(X) 其中 X 的每一個直行即是行向量 xi, i = 1, ..., n,而 u 是一個長度為一的向量,代表最佳的投影方向。你必須使用 fminsearch 指令來進行最佳化。 - Function for min. total distance to a set of points:
Write a function minDist2points(A) that returns a point in a d-dimensional space such that the total distance between this point and all the other $n$ points is minimized, where these $n$ points can be packed into a d-by-n matrix A, with A(:,i) being the i-th point. The initial guess of the solution should be set to the mean of these $n$ points.
Test cases
- minDist2points([1 4 2;8 6 1]) returns [3.2438; 5.7910].
- minDist2points([1 4 2 3; 8 6 1 7; 5 9 0 1]) returns [ 2.2855; 6.3539; 3.6291].
- Function for min. total distance to a set of hyperplanes:
Write a function minDist2hyperplanes(A) that returns a point in a d-dimensional space such that the total distance between this point and all the other $n$ hyperplanes is minimized, where these $n$ hyperlines can be packed into a (d+1)-by-n matrix A, with A(:,i) being the coefficients of the i-th hyperplane: $A(1,i)*x_1+A(2,i)*x_2+\cdots+A(d,i)*x_d+A(d+1,1)=0$.
- Circle fitting via DSS:
A circle in 2D can be described by the following equation
$$(x-a)^2+(y-b)^2=r^2,$$
where $(a, b)$ is the center and $r$ is the radius of the circle. Given a dataset $\{(x_i, y_i)|i=1, 2, ..., n\}$, the sum of distances of these points to the circle can be formulated as follows:
$$
f(a, b, r)=\sum_{i=1}^{n}\left|\sqrt{(x_i-a)^2+(y_i-b)^2}-r\right|
$$
Write a function circleFitByDss.m that can find the best values of $[a, b, r]^T$ such that $f(a, b, r)$ can be minimized. The usage of the function is:
output = circleFitByDss(data) where- data: an 2-by-n dataset matrix, with each column being a sample data point.
- output: a column vector of the derived $[a, b, r]^T$ using Downhill Simplex Search (which is implemented as the function "fminsearch" in MATLAB).
Note that the initial guess of $[a, b, r]^T$ should be as close as possible to the minimizing point. One good choice is to set the center ($[a, b]^T$) as the mean of all the data points, and set $r$ as the average distance of the center to each data point.
Here is a test example:
- Rectangle fitting via DSS:
A rectangle in 2D can be described by 4 parameters $[x, y, \alpha, \beta]$, where $[x, y]$ is the center coordinate of the rectangle, $\alpha$ is the half width, and $\beta$ is the half height. (Thus the 4 corners of the rectangle can be represented by 4 points at $[x-\alpha, y-\beta]$, $[x-\alpha, y+\beta]$, $[x+\alpha, y+\beta]$, and $[x+\alpha, y-\beta]$.)
Given a point in 2D, the distance of this point to the rectangle is defined as the shortest distance of this point to all possible data points on the rectangle.
Write a function rectangleFit.m that can find the best values of $[x, y, \alpha, \beta]^T$ such that the total distance of a dataset to the rectangle can be minimized. The usage of the function is:
output = rectangleFit(data) where- data: an 2-by-n dataset matrix, with each column being a sample data point.
- output: a column vector of the derived $[x, y, \alpha, \beta]^T$ using Downhill Simplex Search (which is implemented as the function "fminsearch" in MATLAB).
Note that the initial guess of $[x, y, \alpha, \beta]^T$ should create a bounding box for the dataset.
Here is a test example:
MATLAB程式設計:進階篇