9-1 x}

在一個矩陣 A 中，位於第 i 橫列、第 j 直行的元素可表示為 A(i, j)，其中 i 與 j 即是此元素的下標（Subscript）或索引（Index）。但在 MATLAB 中，所有矩陣的內部表示法都是以直行為主的一維向量，所以 A(i, j) 和 A(i+(j-1)*m) 是完全一樣的，其中 m 代表矩陣A的列數。換句話說，我們可以使用一維或二維下標來存取矩陣，完全看程式設計者的需求。

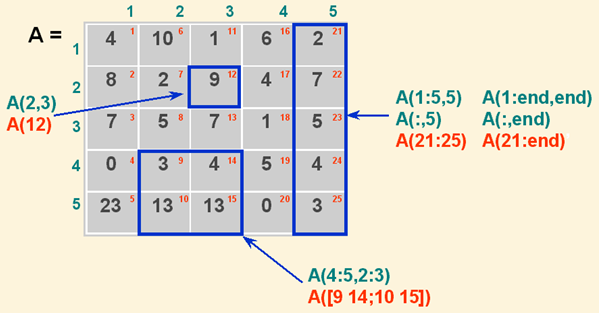
以上圖為例，置於矩陣內部的右上角的小數字代表一維下標，因此 A(2,3)和 A(12) 所指到的元素都是 9，可驗證如下：

Example 1: 09-矩陣的處理與運算/matrix01.m

A = [4 10 1 6 2; 8 2 9 4 7; 7 5 7 1 5; 0 3 4 5 4; 23 13 13 0 3]; A(2,3) - A(12) ans = 0

請特別注意：在本章各節中，會常用到「向量」、「矩陣」及「陣列」，為了避免造成混淆，特別說明如下：

• 向量（Vector）：一維的矩陣，可分為行向量（Column Vectors）及列向量（Row Vectors）。
• 矩陣（Matrices）：二維的陣列，一維向量為其特例。
• 陣列（Arrays）：為矩陣的延伸，可含有 n 維，一般二維矩陣及一維向量均為其特例。

我們可以使用矩陣下標來進行矩陣的索引（Indexing），例如：可以取出矩陣 A 的 第四、五 橫列與 二、三 直行所形成的部份矩陣如下：

Example 2: 09-矩陣的處理與運算/matrix02.m

A = [4 10 1 6 2; 8 2 9 4 7; 7 5 7 1 5; 0 3 4 5 4; 23 13 13 0 3]; B = A(4:5, 2:3) B = 3 4 13 13

我們也可以使用一維下標的方式來達到同樣目的：

Example 3: 09-矩陣的處理與運算/matrix03.m

A = [4 10 1 6 2; 8 2 9 4 7; 7 5 7 1 5; 0 3 4 5 4; 23 13 13 0 3]; B = A([9 14; 10 15]) B = 3 4 13 13

若要取出一整列或一整行，可用冒號（:）來代表所有的列數或行數，例如：欲取出矩陣 A 的第五個直行，可輸入如下：

Example 4: 09-矩陣的處理與運算/matrix04.m

A = [4 10 1 6 2; 8 2 9 4 7; 7 5 7 1 5; 0 3 4 5 4; 23 13 13 0 3]; B = A(:, 5) B = 2 7 5 4 3

亦可使用 end 這個保留字來代表某一維度的最大值，例如：矩陣 A 的第五個直行也可寫成 A(:, end)，例如：

Example 5: 09-矩陣的處理與運算/matrix05.m

A = [4 10 1 6 2; 8 2 9 4 7; 7 5 7 1 5; 0 3 4 5 4; 23 13 13 0 3]; B = A(:, end) B = 2 7 5 4 3

請注意 end 這個保留字的意義是隨位置而變，在上例中，end 代表 5，可是在 A(21:end) 中，end 代表 25，這是因為在矩陣 A 的一維下標中，最大值就是 25。

此外，我們可以直接刪除矩陣的某一整個橫列或直行，例如：

Example 6: 09-矩陣的處理與運算/matrix06.m

A = [4 10 1 6 2; 8 2 9 4 7; 7 5 7 1 5; 0 3 4 5 4; 23 13 13 0 3]; A(2, :) = [] % 刪除 A 矩陣的第二列 A = 4 10 1 6 2 7 5 7 1 5 0 3 4 5 4 23 13 13 0 3

也可以一次刪除矩陣內第二、四、五行的各元素，例如：

Example 7: 09-矩陣的處理與運算/matrix07.m

A = [4 10 1 6 2; 7 5 7 1 5; 0 3 4 5 4; 23 13 13 0 3]; A(:, [2 4 5]) = [] % 刪除 A 矩陣的第二、四、五直行 A = 4 1 7 7 0 4 23 13

也可依次把矩陣 A 和其倒數「並排」起來，得到新矩陣 B，例如：

Example 8: 09-矩陣的處理與運算/matrix08.m

A = [4 1; 7 7; 0 4; 23 13]; B = [A 1./A] % 1./A 是矩陣 A 每個元素的倒數 B = 4.0000 1.0000 0.2500 1.0000 7.0000 7.0000 0.1429 0.1429 0 4.0000 Inf 0.2500 23.0000 13.0000 0.0435 0.0769

Hint

在上例中，由於矩陣 A 含有值為 0 的元素，故對其倒數 1./A 的運算，MATLAB會產生一個「除以零」的回傳警告訊息（即 "Warning: Divide by zero."），但其不影響程式或指令的正常執行。

最後，可用 diag 指令取出矩陣的對角線各元素，例如：

Example 9: 09-矩陣的處理與運算/matrix09.m

B = [0 1 2 3; 2 3 4 5; 5 6 7 8; 7 8 9 0]; d = diag(B) % 取出矩陣 B 的對角線元素 d = 0 3 7 0

也可以用 reshape 指令來改變一個矩陣的維度，例如：

Example 10: 09-矩陣的處理與運算/matrix10.m

B = [0 1 2 3; 2 3 4 5; 5 6 7 8; 7 8 9 0]; C = reshape(B, 2, 8) % 將矩陣 B 排成 2×8 的新矩陣 C C = 0 5 1 6 2 7 3 8 2 7 3 8 4 9 5 0

在上述範例中，MATLAB 會先將矩陣 B 排成一個行向量（即 MATLAB 內部的矩陣表示法），再將此行向量塞成 2×8 的新矩陣。

矩陣索引的技巧可說是千變萬化，若能善用這些技巧，不但能縮短撰寫的程式碼，還能提高程式執行的效能。尤其當您想使用向量化的運算來提高程式效能時，就一定要用到各種矩陣索引技巧。其他矩陣索引技巧，可參見本書姊妹作「MATLAB程式設計：進階篇」的第二章「程式碼與記憶體之最佳化」。

---

MATLAB程式設計：入門篇