Chapter 6: Exercises

Part 1

  1. 以電影方式產生包含 21 個畫面的動畫，代表 peaks 曲面乘上 a，其中 a 的值由 -1 至 1 等分切成 21 點。
  2. 以物件方式產生動畫，呈現一個小圓（半徑為 1）在一個大圓（半徑為 3）的圓周外部滾動的動畫。

    06-動畫製作/myMovie02.mclose all theta = linspace(0, 2*pi); r1 = 3; x1 = r1*cos(theta); y1 = r1*sin(theta); plot(x1, y1), axis image % 大圓 r2 = 1; center = (r1+r2)*[1, 0]; x2 = r2*cos(theta); y2 = r2*sin(theta); h = line(center(1)+x2, center(2)+y2, 'EraseMode', 'xor', 'color', 'r'); % 小圓 axis([-5 5 -5 5]); % 設定圖軸的範圍 n = 5; % 轉5圈 theta1 = linspace(0, n*2*pi, n*2000); for i = 1:length(theta1); center = (r1+r2)*[cos(theta1(i)), sin(theta1(i))]; set(h, 'xdata', center(1)+x2, 'ydata', center(2)+y2); % 設定小圓的 x, y 座標 drawnow % 立即作圖 end

    若以極座標（複數）來進行資料處理，程式碼會比較簡單一些，如下。

    06-動畫製作/myMovie02_2.mclose all theta = linspace(0, 2*pi); r1 = 3; circle1 = r1*exp(sqrt(-1)*theta); % 大圓 plot(circle1), axis image r2 = 1; circle2 = r2*exp(sqrt(-1)*theta); % 小圓 center = r1+r2; h = line(real(center+circle2), imag(center+circle2), 'EraseMode', 'xor', 'color', 'r'); axis([-5 5 -5 5]); % 設定圖軸的範圍 n = 5; % 轉5圈 theta1 = linspace(0, n*2*pi, n*2000); for i = 1:length(theta1); center = (r1+r2)*exp(sqrt(-1)*(theta1(i))); set(h, 'xdata', real(center+circle2), 'ydata', imag(center+circle2)); % 設定小圓的 x, y 座標 drawnow % 立即作圖 end

  3. 以物件方式產生動畫，呈現一個小圓（半徑為 1）在一個大圓（半徑為 3）的圓周內部滾動的動畫。
  4. 以物件方式產生動畫，呈現一個小圓（半徑為 1）在一個中圓（半徑為 3）的圓周內部滾動，且此中圓又在一個大圓（半徑為 5）的圓周內部滾動的動畫。
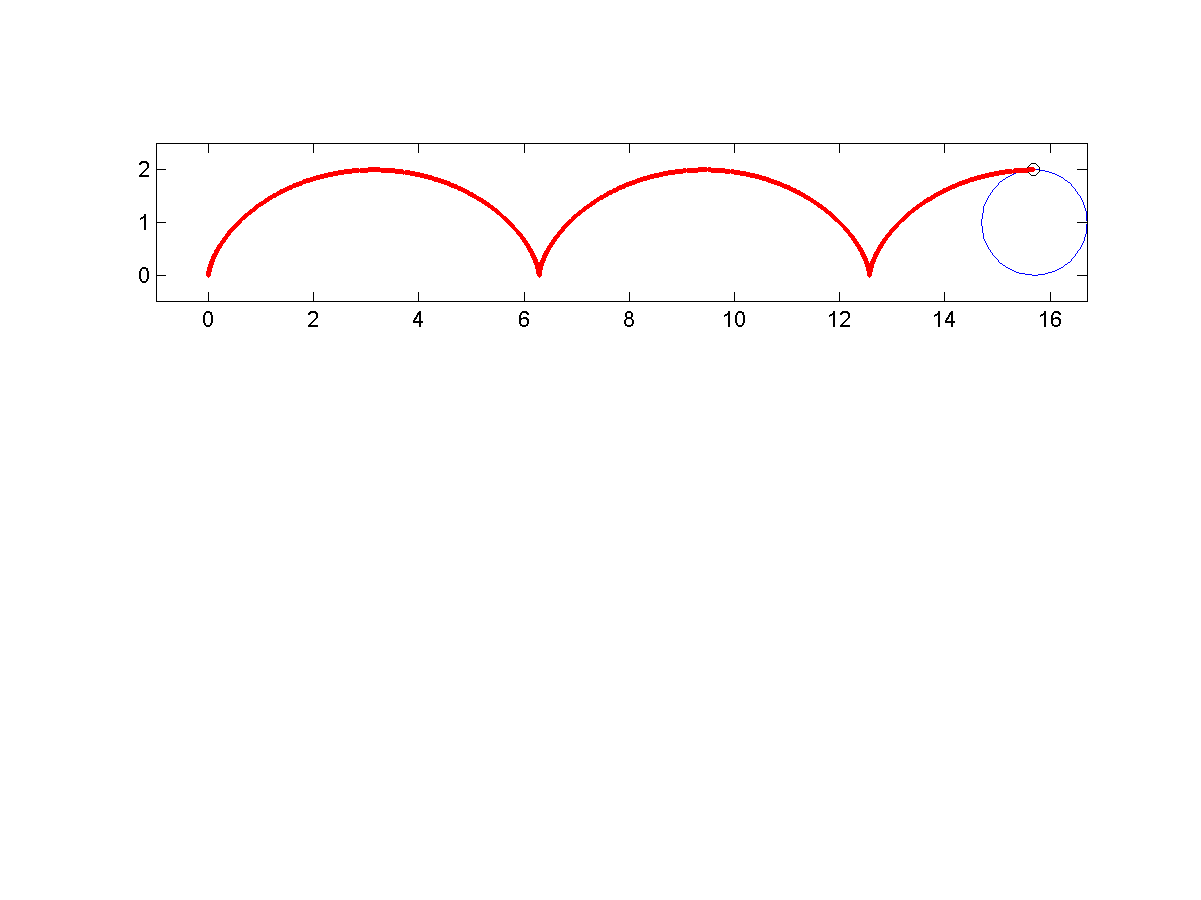
  5. 以物件方式產生動畫，呈現一個圓圈（半徑為 1）由畫面左邊滾到右邊，圓周上的任一點所拉出的一條擺線。

    06-動畫製作/cycloid02.m% 擺線的動畫, Roger Jang, 20050208 x = linspace(0, 5*pi, 2000); theta = linspace(0, 2*pi); r = 1; circle = j+r*exp(sqrt(-1)*theta); subplot(2,1,1); circleH=plot(circle); axis image set(circleH, 'erase', 'xor'); axis([min(x)-r, max(x)+r, -0.5, 2*r+0.5]); dot1H=line(0, 0, 'marker', 'o', 'color', 'k', 'erase', 'xor'); dot2H=line(0, 0, 'marker', '.', 'color', 'r', 'erase', 'none'); for i=1:length(x) set(circleH, 'xdata', x(i)+real(circle)); angle=-pi/2-x(i); set(dot1H, 'xdata', x(i)+cos(angle), 'ydata', r+sin(angle)); set(dot2H, 'xdata', x(i)+cos(angle), 'ydata', r+sin(angle)); % line('xdata', x(i)+cos(angle), 'ydata', r+sin(angle), 'color', 'r', 'marker', '.'); drawnow end

    產生圖形如下：

  6. 以物件的方式產生動畫，呈現下列方程式： $$ y=cos^2(x+k)e^{-x/5} $$ 讓 k 隨時間而變大，來顯示此方程式的動畫。

    06-動畫製作/myMovie06.mx = 0:0.1:8*pi; k = 0; h = plot(x, cos(x+k).*cos(x+k).*exp(-x/5), 'EraseMode', 'xor'); axis([-inf inf -1 1]); % 設定圖軸的範圍 grid on % 畫出格線 for k = 1:0.01:50 y = cos(x+k).*cos(x+k).*exp(-x/5); set(h, 'ydata', y); % 設定新的 y 座標 drawnow % 立即作圖 end

    Part 2

    1. XOR identity: For any logical variables x and y, prove the following identities:
      1. x ♁ y ♁ y = x
      2. ((x ♁ y)' ♁ y)' = x
    2. 外部花瓣線: 以物件方式產生動畫，呈現一個小圓（半徑為 1）在一個大圓（半徑為 5）的圓周外部滾動的動畫，並畫出小圓圓周任一點所形成的「外部花瓣線」。
    3. 內部花瓣線: 以物件方式產生動畫，呈現一個小圓（半徑為 1）在一個大圓（半徑為 5）的圓周內部滾動的動畫，並畫出小圓圓周任一點所形成的「內部花瓣線」。
      提示：Hypocycloid on Wiki、Spirograph
    4. 花瓣線之花瓣個數: 小圓在大圓的內部或外部滾動，會形成花瓣線。若大圓和小圓的半徑分別是 m 公分及 n 公分（其中 m 和 n 都是整數），請問
      1. 小圓必須在大圓內至少繞大圓圓心幾周，才會形成封閉的花瓣線？
      2. 這個封閉的花瓣線有幾個花瓣？
    5. 粒子碰撞動畫: 三個圓圈（半徑為1）在一個邊長為 10 的方形內進行碰撞，假設這三個圓圈的速度一樣（都是每秒10單位），質量也一樣，但運動方向及開始位置都是由亂數產生，請以MATLAB呈現此動畫。
      提示：在發生碰撞時，兩球沿著切向量的速度不變，沿著法向量的速度變化則依循一維彈性碰撞的原則而定，相關方程式可見此說明（local copy、公式推導）。
    MATLAB程式設計：入門篇