Chapter 3: Exercises

Part 1

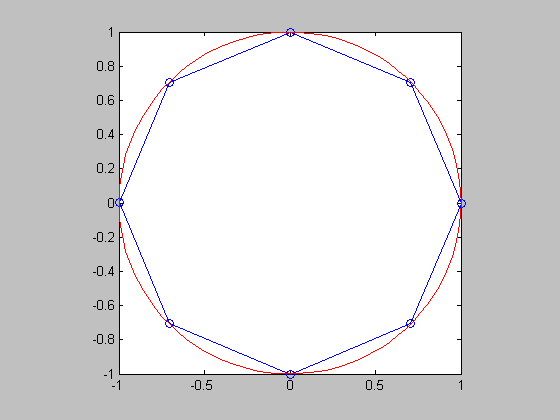
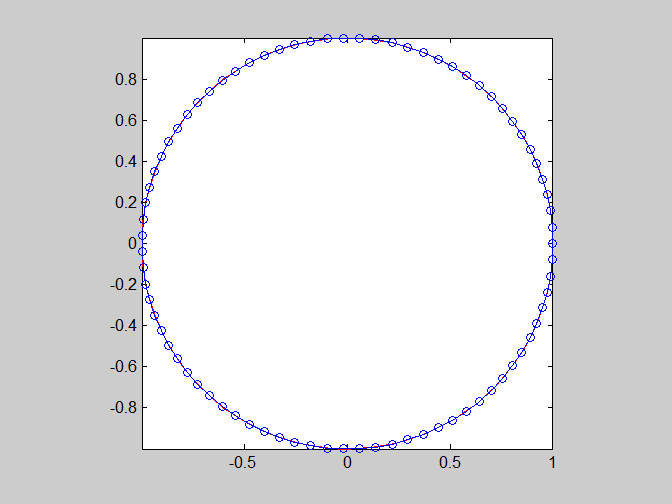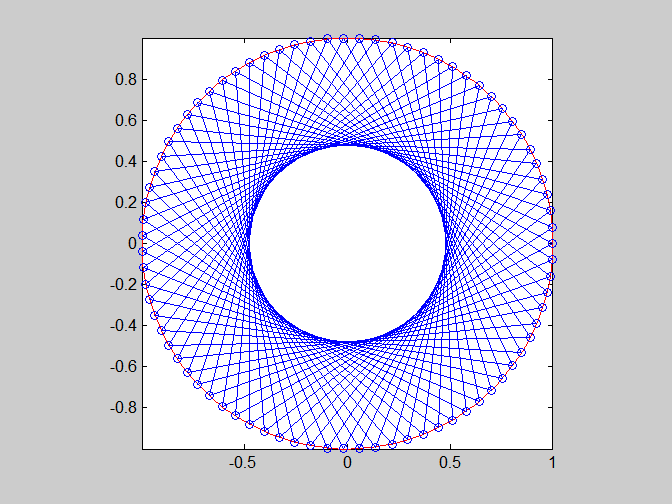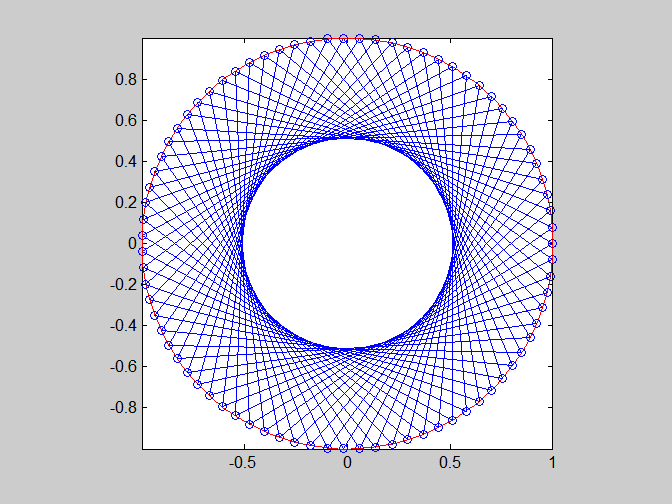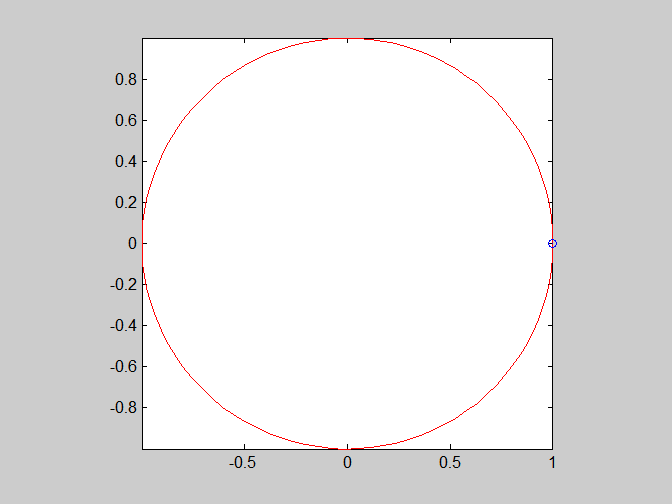
  1. 試寫一函數 regPolygon(n)，其功能為畫出一個圓心在 (0, 0)、半徑為 1 的圓，並在圓內畫出一個內接正 n 邊形，其中一頂點位於 (1, 0)。例如 regPolygon(8) 可以畫出如下之正八邊型：

    Example 1: 03-二維平面繪圖/regPolygon.mfunction regPolygon(n) % regPolygon: 畫正多邊型及其外接圓 if nargin<1, n=8; end % ====== 畫正多邊型 vertices=exp((0:n)*j*2*pi/n); plot(vertices, '-o'); % ====== 畫外接圓 hold on theta=linspace(0, 2*pi); plot(exp(j*theta), '-r'); hold off axis image

  2. 一條參數式的曲線可由下列方程式表示：
    x = sin(t), y = 1 - cos(t) + t/10
    當 t 由 0 變化到 4*pi 時，請寫一個 MATLAB 的腳本 plotParam.m，畫出此曲線在 XY 平面的軌跡。

    Example 2: 03-二維平面繪圖/plotParam.mt = linspace(0, 4*pi); x = sin(t); y = 1-cos(t)+t/10; plot(x, y, '-o');

  3. 試寫一函數 regStar(n)，其功能為畫出一個圓心在 (0, 0)、半徑為 1 的圓，並在圓內畫出一個內接正 n 星形，其中一頂點位於 (1, 0)。例如 regStar(7) 可以畫出如下之正 7 星型：

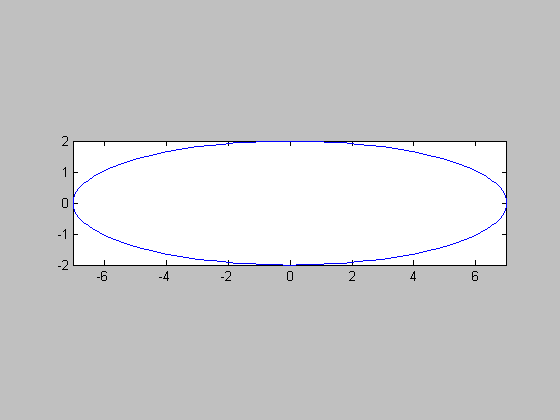
    Example 3: 03-二維平面繪圖/regStar.mfunction regStar(n) if nargin<1, n=7; end vertices=[1]; for i=1:n step=2*pi*floor(n/2)/n; vertices=[vertices, exp(i*step*sqrt(-1))]; end plot(vertices, '-o'); % 畫外接圓 hold on theta=linspace(0, 2*pi); plot(cos(theta), sin(theta), '-r'); hold off axis image

  4. 一個平面上的橢圓可以表示成下列方程式：
    (x/a)2+(y/b)2=1
    我們也可以用參數式將橢圓表示成：
    x = a*cos(t)
    y = a*sin(t)
    請利用上述參數式，寫一個函數 ellipse(a, b)，其功能是畫出一個橢圓，而且橢圓上共有100個點。例如，ellipse(7, 2) 可以產生下列圖形：

    Example 4: 03-二維平面繪圖/ellipse.mfunction ellipse(a, b) if nargin<1, a=7; end if nargin<2, b=2; end % 畫橢圓 theta=linspace(0, 2*pi, 101); plot(a*cos(theta), b*sin(theta)); axis image

  5. 請用寫一個 MATLAB 腳本 figSolve.m，利用圖解法，說明下列聯立方程式有無窮多組解：
    y = x
    y = sin(1/x)
    （請務必畫出上述兩條曲線來加以說明之。）

    Example 5: 03-二維平面繪圖/figSolve.mbound=[eps, 0.1]; fplot('sin(1/x)', bound, 1e-4); hold on fplot('x', bound); hold off

  6. 利薩如圖形（Lissajous Figure，又稱為 Bowditch Curve）可用下列參數式來表示：
    x = cos(m*t)
    y = sin(n*t)
    試畫出在不同 m、n 值的利薩如圖形：
    1. m = n = 1
    2. m = 3, n = 2
    3. m = 2, n = 7
    4. m = 10, n = 11

    Example 6: 03-二維平面繪圖/lissajousFigure.mt=linspace(0, 2*pi, 1000); subplot(2,2,1); m=1; n=1; x=cos(m*t); y=sin(n*t); plot(x, y); title('m=1, n=1'); axis image subplot(2,2,2); m=3; n=2; x=cos(m*t); y=sin(n*t); plot(x, y); title('m=3, n=2'); axis image subplot(2,2,3); m=2; n=7; x=cos(m*t); y=sin(n*t); plot(x, y); title('m=2, n=7'); axis image subplot(2,2,4); m=10; n=11; x=cos(m*t); y=sin(n*t); plot(x, y); title('m=10, n=11'); axis image

  7. Chebyshev 多項式的定義如下：
    y = cos(m*cos-1x)
    其中 x 的值介於 [-1, 1]。當 m 的值由 1 變化到 5，我們可得到五條曲線。請將這五條曲線畫在同一張圖上面，記得要使用 legend 指令來標明每一條曲線。

    Example 7: 03-二維平面繪圖/chebyshevPlot.mx=linspace(-1, 1)'; y=[]; for m=1:5 y=[y, cos(m*acos(x))]; end plot(x, y); legend('m=1', 'm=2', 'm=3', 'm=4', 'm=5'); axis image

  8. 使用 MATLAB 畫一個圓心在原點、半徑等於 10 的圓，並在圓周上依逆時鐘方向取 任意四點 A、B、C、D，將線段 AB、AC、AD、BC、BD、CD 用直線畫出。
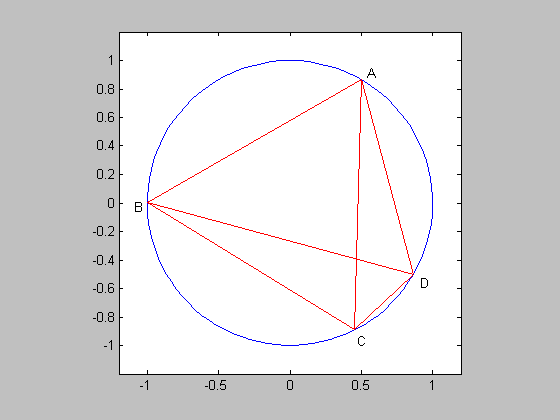
    1. 計算線段 AB、AC、AD、BC、BD、CD 的長度。
    2. 計算 AB*CD+AD*BC 和 AC*BD。兩者的差距有多少？是否可視為相等？
    （上述定理稱為 Ptolemy 定理，你若能用國中所學的古典幾何方式來證明此定理，將有加分。）

    Example 8: 03-二維平面繪圖/ptolemy2.mclear all; t=linspace(0, 2*pi); r=10; x=r*cos(t); y=r*sin(t); a=r*[cos(0.50*pi), sin(0.50*pi)]; b=r*[cos(0.90*pi), sin(0.90*pi)]; c=r*[cos(1.25*pi), sin(1.25*pi)]; d=r*[cos(1.80*pi), sin(1.80*pi)]; plot(x, y, 'b', a(1), a(2), '.k', b(1), b(2), '.k', c(1), c(2), '.k', d(1), d(2), '.k'); axis image text(a(1), a(2), ' A'); text(b(1), b(2), ' B'); text(c(1), c(2), ' C'); text(d(1), d(2), ' D'); line([a(1), b(1)], [a(2), b(2)], 'color', 'r'); t=(a+b)/2; text(t(1), t(2), 'AB'); line([b(1), c(1)], [b(2), c(2)], 'color', 'r'); t=(b+c)/2; text(t(1), t(2), 'BC'); line([c(1), d(1)], [c(2), d(2)], 'color', 'r'); t=(c+d)/2; text(t(1), t(2), 'CD'); line([d(1), a(1)], [d(2), a(2)], 'color', 'r'); t=(d+a)/2; text(t(1), t(2), 'DA'); line([a(1), c(1)], [a(2), c(2)], 'color', 'r'); t=(a+c)/2; text(t(1), t(2), 'AC'); line([b(1), d(1)], [b(2), d(2)], 'color', 'r'); t=(b+d)/2; text(t(1), t(2), 'BD'); ab=norm(a-b); bc=norm(b-c); cd=norm(c-d); ad=norm(a-d); ac=norm(a-c); bd=norm(b-d); fprintf('ab = %f\n', ab); fprintf('bc = %f\n', bc); fprintf('cd = %f\n', cd); fprintf('ad = %f\n', ad); fprintf('ac = %f\n', ac); fprintf('bd = %f\n', bd); fprintf('ab*cd = %f\n', ab*cd); fprintf('ad*bc = %f\n', ad*bc); fprintf('ac*bd = %f\n', ac*bd); fprintf('ab*cd+ad*bc-ac*bd = %f\n', ab*cd+ad*bc-ac*bd);ab = 11.755705 bc = 10.449971 cd = 15.208119 ad = 17.820130 ac = 18.477591 bd = 19.753767 ab*cd = 178.782165 ad*bc = 186.219852 ac*bd = 365.002017 ab*cd+ad*bc-ac*bd = 0.000000

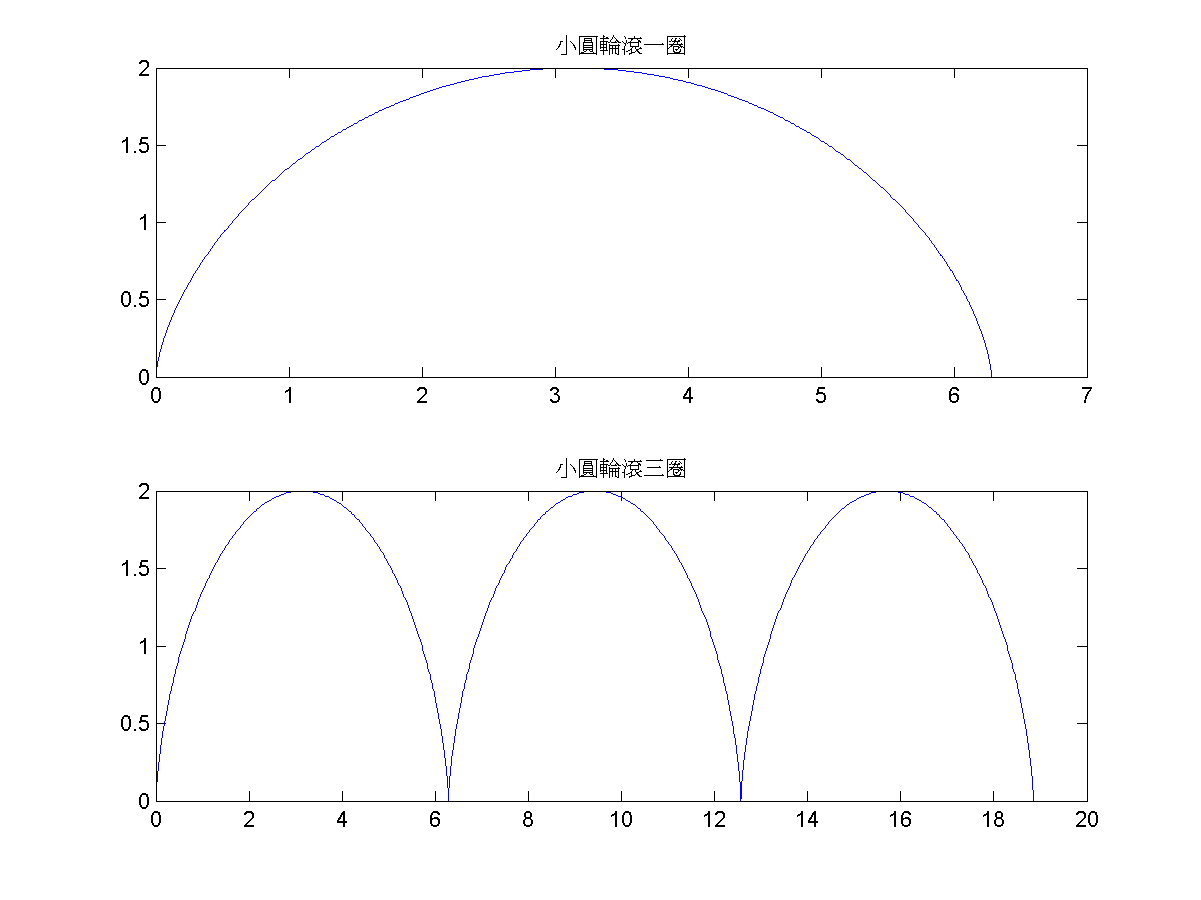
  9. 當一個小圓輪在平面上滾動時，輪緣的一點在滾動時所形成的軌跡稱為「擺線」（Cycloid）。請用 MATLAB 畫出一個典型的擺線，其中小圓輪的半徑為 1，而且至少要滾三圈。產生圖形如下：

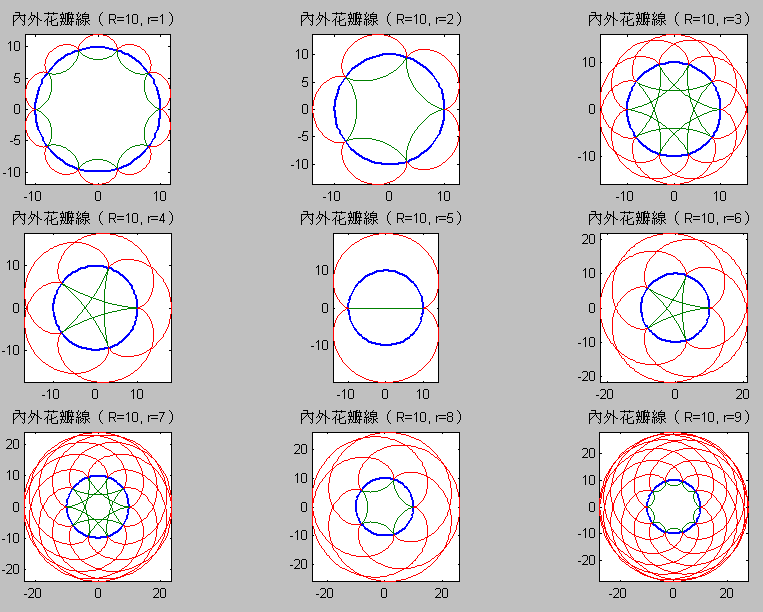
    Example 9: 03-二維平面繪圖/cycloid01.mclear all; r=1; t1=linspace(0,2*pi,1000); t2=linspace(0,6*pi,1000); x1=r*(t1-sin(t1)); y1=r*(1-cos(t1)); x2=r*(t2-sin(t2)); y2=r*(1-cos(t2)); subplot(2,1,1);plot(x1,y1); title('小圓輪滾一圈'); subplot(2,1,2);plot(x2,y2); title('小圓輪滾三圈');

  10. 此題和上題類似。當一個小圓輪沿著一條曲線行進時，輪緣任一點的軌跡就會產生變化豐富的擺線。假設小圓輪的半徑 r=2。
    1. 當小圓輪繞著一個大圓（半徑 R=5）的外部滾動時，請畫此「圓輪擺線」或「外花瓣線」。
    2. 重複上小題，但改成在大圓的內部滾動，請畫出此「內花瓣線」。

    Hint
    下圖顯示在不同的 R 和 r 值，所產生的圓輪擺線。

    Example 10: 03-二維平面繪圖/petalPlot01.mR=5; % 大圓半徑 r=2; % 小圓半徑 n=r/gcd(r, R); % 圈數 t=linspace(0, n*2*pi, 1000); c=R*exp(i*t); % 內花瓣線 c1=(R-r)*exp(i*t)+r*exp(i*(-R*t/r+t)); % 外花瓣線 c2=(R+r)*exp(i*t)+r*exp(i*(pi+R*t/r+t)); plot(real(c), imag(c), real(c1), imag(c1), real(c2), imag(c2)); axis image title('內花瓣線（綠色）和外花瓣線（紅色）');

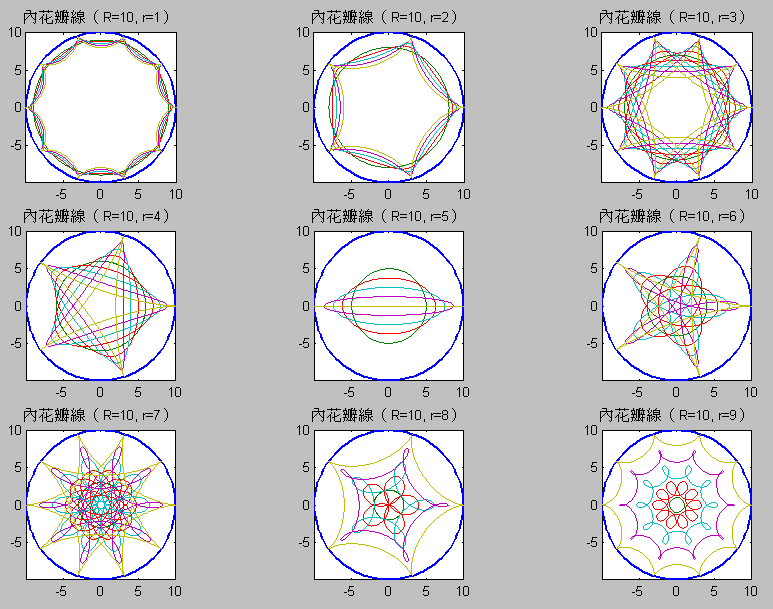
  11. 若大圓和小圓的半徑成整數比，當小圓在大圓的內部滾動時，小圓內的任一點 A 的軌跡就會形成一個漂亮無缺的花瓣線。當大圓半徑 R 為 10，小圓半徑 r 為 3，且 A 點離小圓圓心距離 r1 為 2 時，請畫出此完整的花瓣線。

    Hint
    下圖顯示在不同 r1 值所產生的內花瓣線。

    Hint
    下圖顯示在不同 r1 值所產生的外花瓣線。

    Example 11: 03-二維平面繪圖/petalPlot02.mr=3; % 小圓半徑 R=10; % 大圓半徑 d=2; % 筆心離小圓圓心距離 n=r/gcd(r, R); % 圈數 t=linspace(0, n*2*pi, 1000); c=R*exp(i*t); % 內花瓣線 c1=(R-r)*exp(i*t)+d*exp(i*(-R*t/r+t)); % 外花瓣線 c2=(R+r)*exp(i*t)+d*exp(i*(pi+R*t/r+t)); plot(real(c), imag(c), real(c1), imag(c1), real(c2), imag(c2)); axis image title('內花瓣線（綠色）和外花瓣線（紅色）');

Part 2

  1. Simple plots by hands: Please presume you are MATLAB to plot the result of the following commands using a pen. Here we have a = [1 2; 3 4]. (Please remember to write down the coordinates of the endpoints of each line.)
    1. plot(a);
    2. plot(a');
    3. plot(a, a');
    4. plot(a, a', a', a);
  2. Ellipse plots by hands: Please presume you are MATLAB to plot the result of the following commands using a pen. Here we have t = linspace(0, 2*pi).
    1. x=cos(t); y=sin(t); plot(x, y);
    2. x=cos(t); y=2*sin(t); plot(x, y);
    3. x=2*cos(t); y=sin(t); plot(x, y);
  3. Lissajous figures by hands: Please presume you are MATLAB to plot the result of the following commands using a pen. Here we have t = linspace(0, 2*pi).
    1. x=cos(t); y=sin(t); plot(x, y);
    2. x=cos(t); y=sin(2*t); plot(x, y);
    3. x=cos(2*t); y=sin(t); plot(x, y);
  4. Histogram plots: Determine which one of the following plot is most likely to be generated by each of the following commands:
    1. x=rand(10000, 1); hist(x, 100);
    2. x=randn(10000, 1); hist(x, 100);
    3. x=rand(10000, 1); hist(x.^3, 100);
    4. x=randn(10000, 1); hist(x.^3, 100);
    5. x=rand(10000, 1); hist(nthroot(x, 3), 100);
    6. x=randn(10000, 1); hist(nthroot(x, 3), 100);

  5. Euler's formula:
    1. What is Euler's formula?
    2. How can you prove it? (Hint: Use Taylor series expansion.)
    3. Use the formula to prove that $e^{i\pi}+1=0$.
    4. Use the formula to prove that $\cos(3\theta)=4 \cos(3\theta)-3 \cos \theta$.
  6. Equivalence between polar and plot: Explain why the following two commands will generate same plot (on different coordinate systems), assuming θ is a vector and r(θ) is a function of θ.
    1. polar(θ, r(θ));
    2. plot(r(θ).*exp(j*θ));
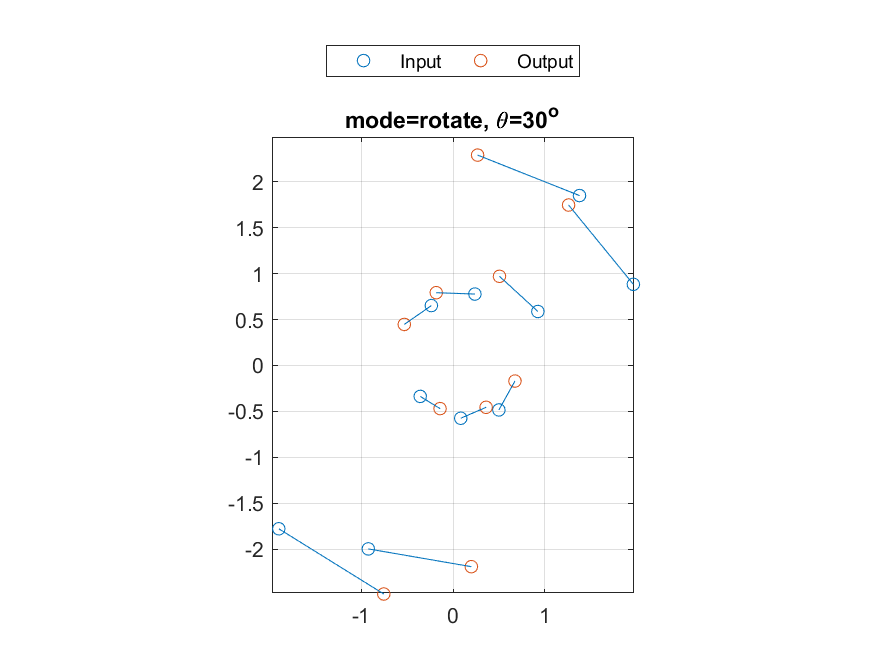
  7. Rotation and reflection: Write a MATLAB function myTransform.m to rotate or reflect a set of 2D points. The usage of the function is
    output=myTransform(vec, theta, mode)
    where
    • vec: a 2-by-n vector representing n points in 2D space
    • theta: angle (counter-clockwise, in radian) for rotation or reflection. For rotation, theta is the rotation angle. For reflection, it is the angle of the reflection axis.
    • mode: 'rotate' for rotation, 'reflect' for reflection
    • output: a 2-by-n vector representing the given n points after rotation or reflection

    Hint
    • For string comparison, you can use "strcmp".
    • It'll be easier to use complex numbers in MATLAB.

    Here is a test case for 'rotate':

    • Inputs:
      • vec=[-0.235892197136722 1.96453251156114 0.0845369570761526 0.499750630743405 0.238445635648528 0.924272931895896 1.3779342772046 -1.89766476744468 -0.922641236606734 -0.357100057722689;0.652821094952841 0.884584173475766 -0.574514061258489 -0.484104482611851 0.778248191474934 0.588137914293571 1.85120493279698 -1.77868417910781 -1.99792708362756 -0.336400759888822];
      • theta=pi/6;
      • mode='rotate';
    • Output:
      • output=[-0.530699182751349 1.25904297483451 0.360468183015827 0.674848983087011 -0.182624117844313 0.506374881905385 0.267723622406047 -0.754083806919876 0.19993279233326 -0.141057341736327;0.447413553787173 1.74833862179625 -0.455275293343144 -0.169371464656083 0.793205522090853 0.971478840654975 2.29215763801555 -2.48921806813918 -2.19157622763379 -0.469881632777453].

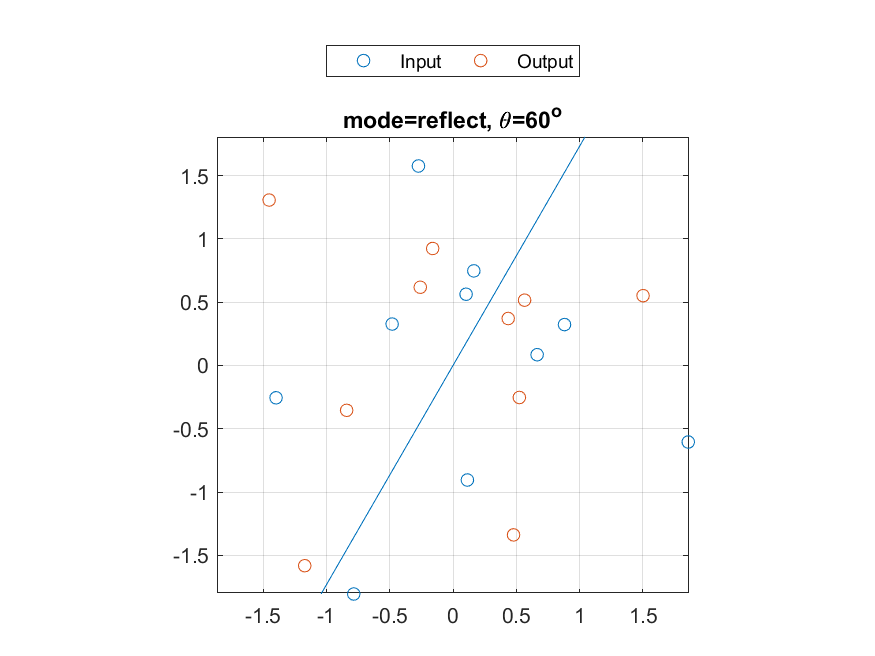
    And here is a test case for 'reflect':

    • Inputs:
      • vec=[-1.39813787581107 0.164404073318729 -0.273046949402907 -0.480937151778845 0.664734120627595 0.880952785381048 -0.784146183664088 1.85859294855571 0.103359722310648 0.113596996734002;-0.255055179880806 0.747734028808123 1.57630014654608 0.327512120829686 0.0851885927211602 0.323213137847597 -1.80537335138609 -0.604530088774459 0.563166955145978 -0.904726212798032];
      • theta=pi/3;
      • mode='reflect';
    • Output:
      • output=[0.478184672761947 0.565354627562556 1.50163944559949 0.524102392575249 -0.258591574904627 -0.160565604477623 -1.17142609378376 -1.4528348885086 0.436037028573025 -0.840314382119783;-1.338350508386 0.51624511838372 0.551684478664278 -0.252747730649369 0.618270931586387 0.924534060598447 -1.58177719102676 1.30732366435664 0.371095622822115 -0.353985221433752].

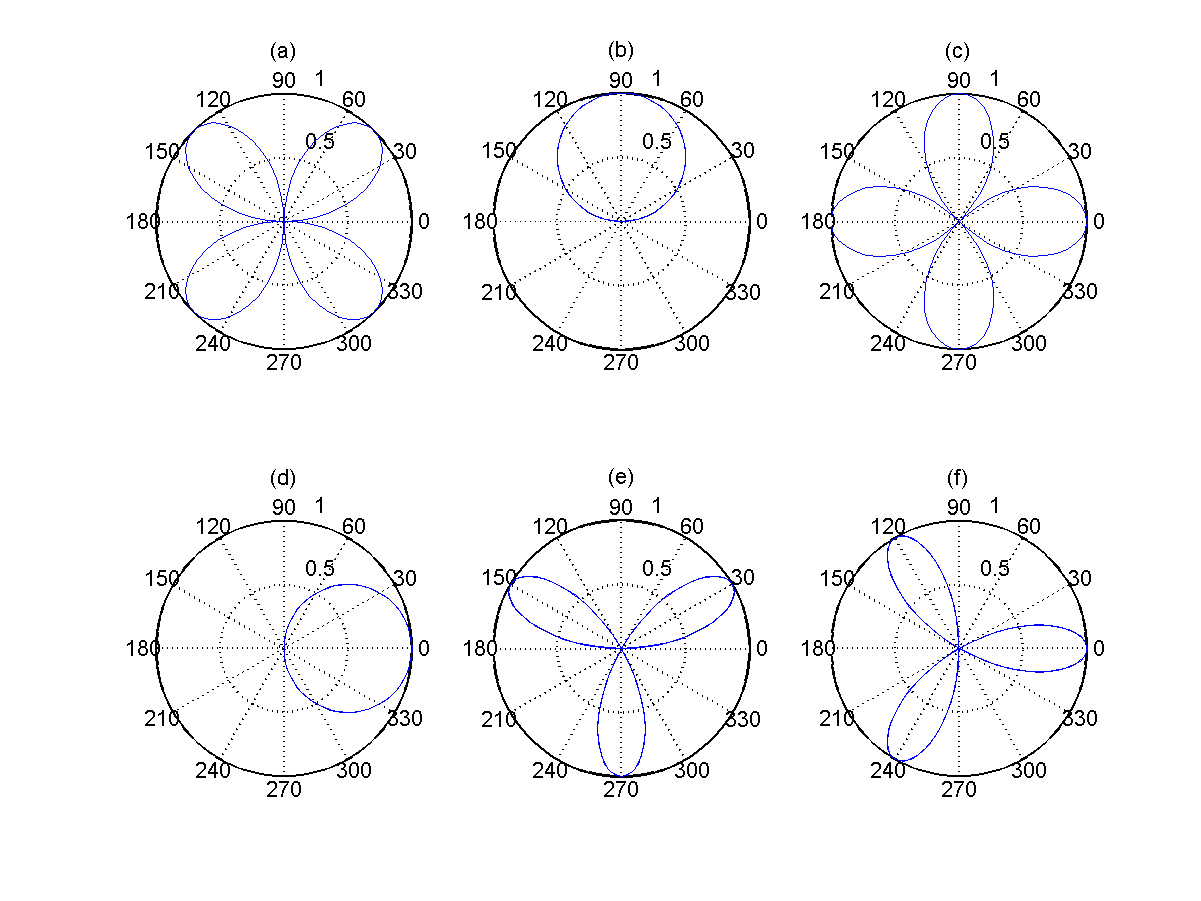
    (Note that the plots are only for reference. You don't need to generate the plots.)
  8. Plots of rose curves: Determine which one of the following plot is most likely to be generated by each of the following commands:
    1. theta=linspace(0, 2*pi); polar(theta, cos(theta));
    2. theta=linspace(0, 2*pi); polar(theta, sin(theta));
    3. theta=linspace(0, 2*pi); polar(theta, cos(2*theta));
    4. theta=linspace(0, 2*pi); polar(theta, sin(2*theta));
    5. theta=linspace(0, 2*pi); polar(theta, cos(3*theta));
    6. theta=linspace(0, 2*pi); polar(theta, sin(3*theta));

  9. Sketch of rose curves: Please use the method of "描點作圖" to sketch the following rose curves in the polar coordinate system, assuming the range of θ is between 0 and 2*pi.
    1. r = cos(θ)
    2. r = cos(2θ)
    3. r = cos(3θ)
    4. r = sin(θ)
    5. r = sin(2θ)
    6. r = sin(3θ)

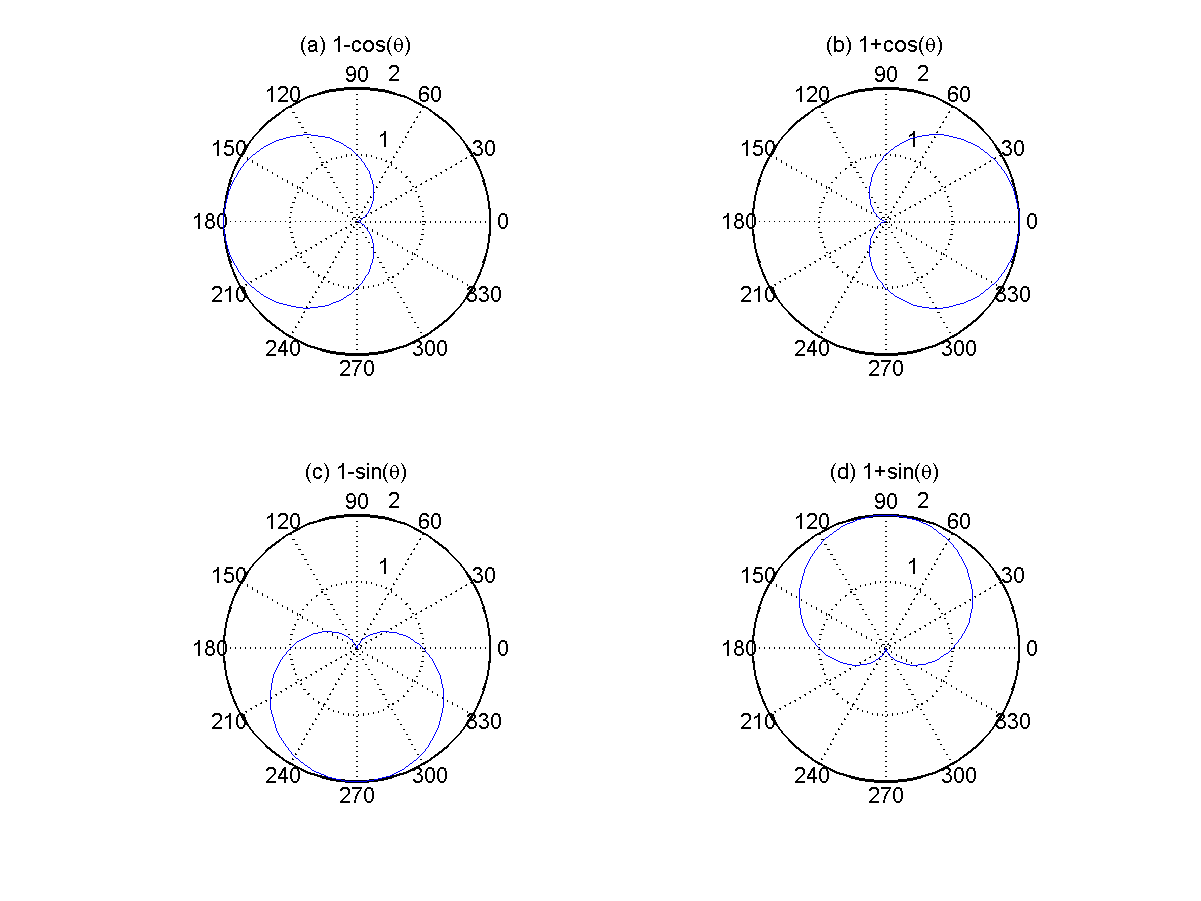
  10. Sketch of cardioids: Please use the method of "描點作圖" to sketch the following cardioids (心臟線) in the polar coordinate system, assuming the range of θ is between 0 and 2*pi.
    1. r = 1 - cos(θ)
    2. r = 1 + cos(θ)
    3. r = 1 - sin(θ)
    4. r = 1 + sin(θ)

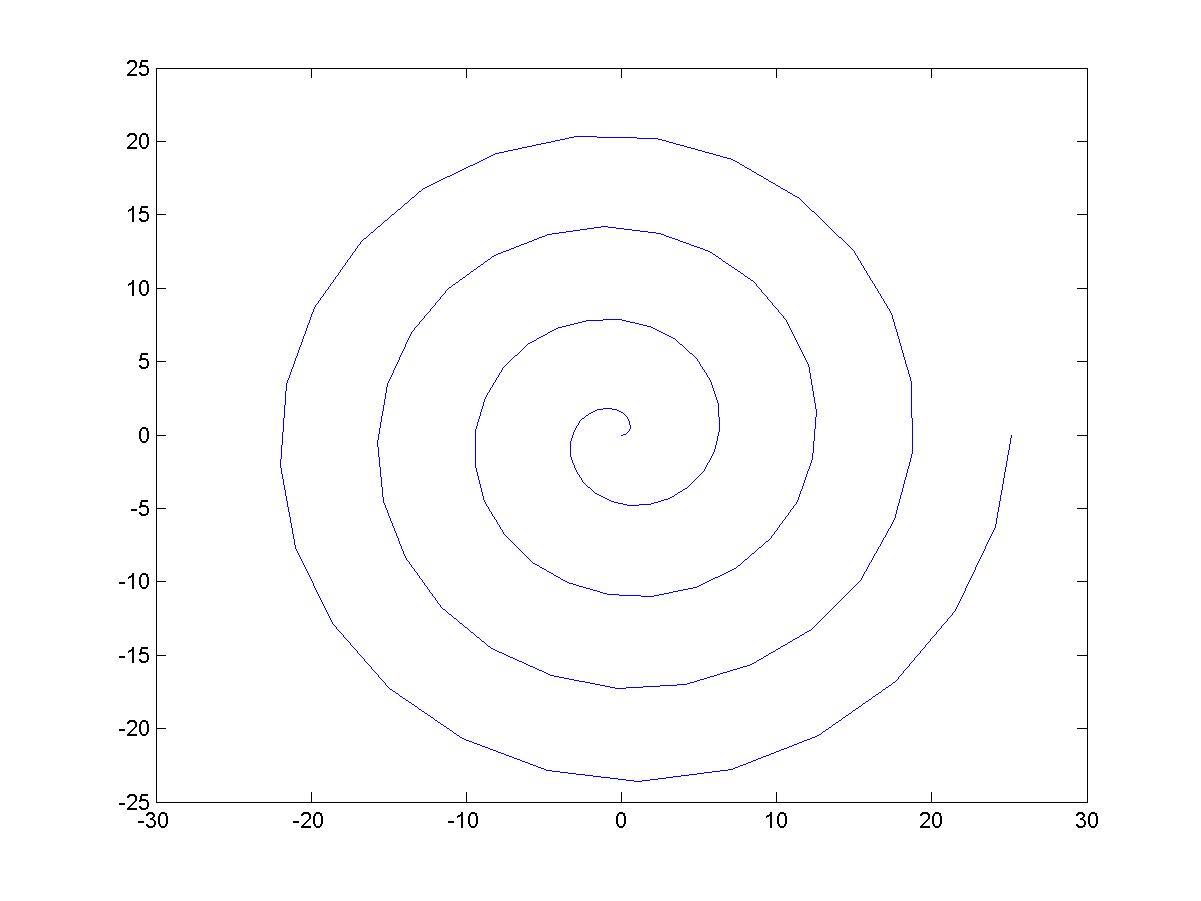
  11. Plot of a simple spiral: 請使用 MATLAB 的兩個指令，分別在平面上畫出螺旋圖，從原點開始，逐漸向外繞圈擴散，圖形如下。（提示：若以極座標來想像，則 r 和 θ 都是必須是隨時間而遞增的函數。）
    1. 使用 plot 指令，畫出圖形如下：

    2. 使用 polar 指令，畫出圖形如下：

    Which command do you think is easier to generate such a plot?
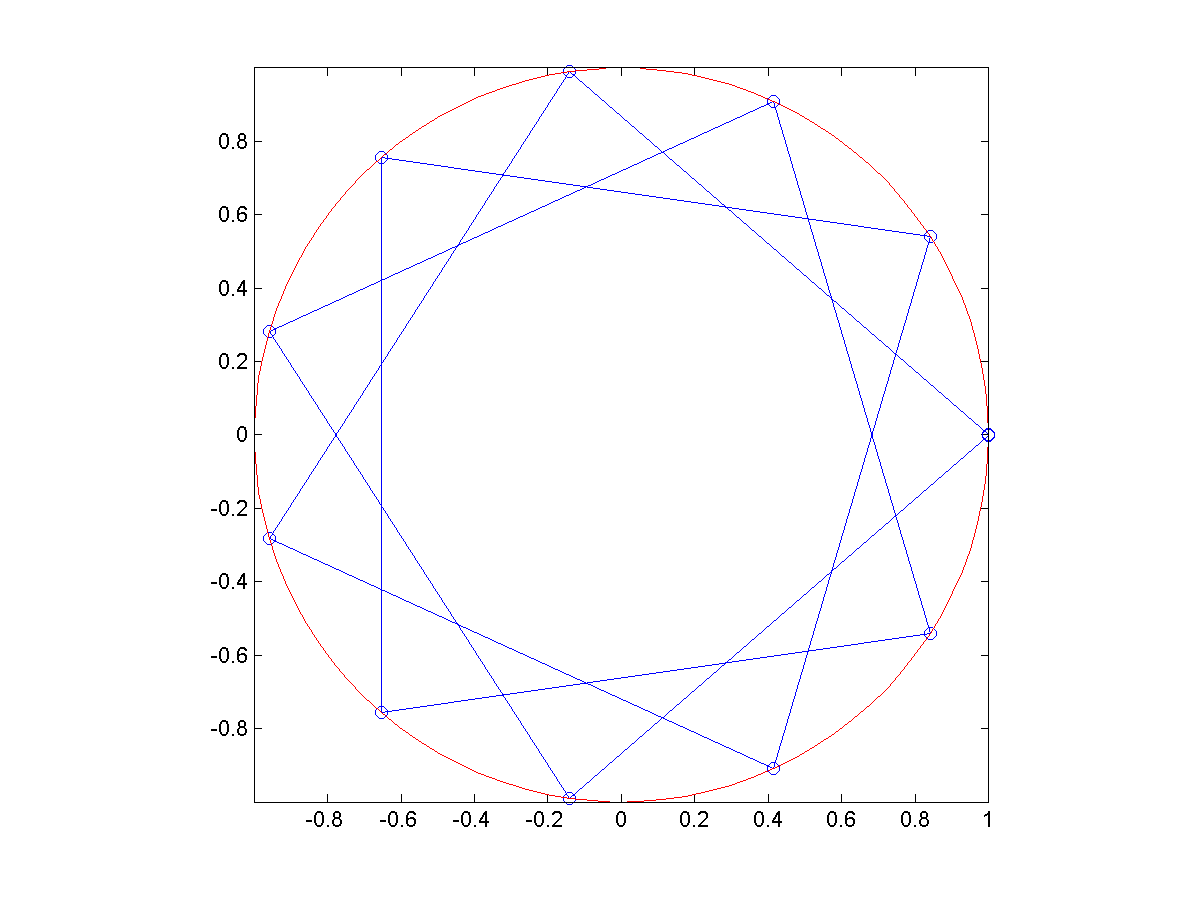
  12. Plot general regular stars:
    1. 試寫一函數 regGeneralStar(n, k)，其功能為畫出一個圓心在 (0, 0)、半徑為 1 的圓，並在圓內畫出一個內接星形，其中一頂點位於 1+0*i（複數表示法），下一頂點則位於 exp(i*2*pi*k/n)，依此類推。例如 regGeneralStar(11, 3) 可以畫出如下之圖形：

    2. Please try the following code to show some animation: 
      for i=1:1000
	regGeneralStar(79, i);
	drawnow
end
      Please convert the animation into an animated gif file, using any resources you can find over the internet. You gif file should look like this:

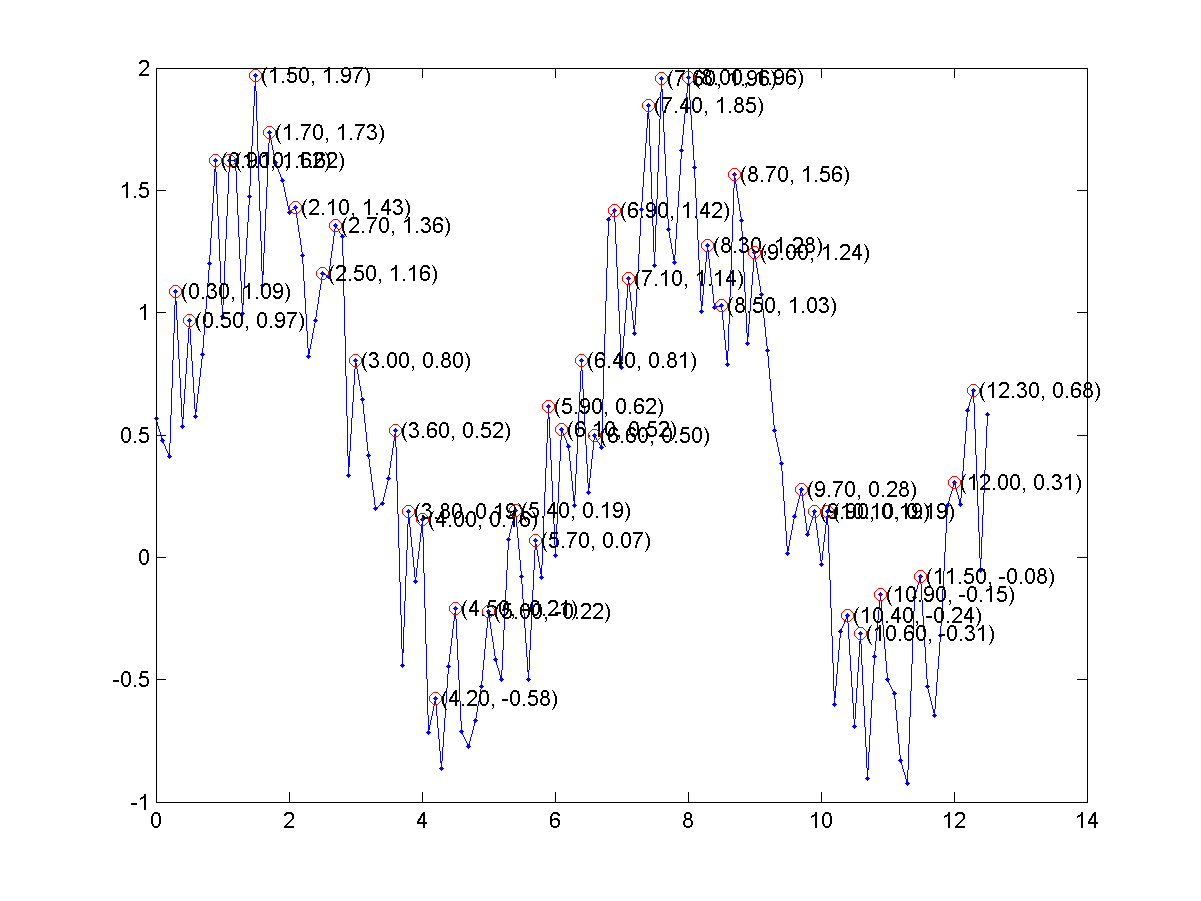
  13. Plot and annotate local maxima: In this exercise, you are going to identify and annotate local maxima.
    1. Plot a sine wave as follows: 
      t=0:0.1:4*pi;
y=sin(t)+rand(1, length(t));
plot(t, y, '.-');
    2. Put a circle at each local maximum.
    3. Use the command "text" to annotate each local maximum, as follows:

  14. Plot Bezier curves: The concept of the Bezier curve is described in the wikipedia.
    1. Plot 5 randomly generated data points on the x-y plane and connect them with straight lines. Be sure to label the data points as p1, p2, p3, p4, and p5.
    2. Draw a 4th-order Bezier curve on top of the above 5 data points.
MATLAB程式設計：入門篇