

| MATLAB Function Reference |   |
Sparse reverse Cuthill-McKee ordering
Syntax
r = symrcm(S)
Description
r = symrcm(S)
回傳 S 的 symmetric reverse Cuthill-McKee ordering。而產生的 r
可使得 S(r,r) 在對角線附近有非零值的元素。對於???(long, skinny problems)來說,在做 LU 或 Cholesky
分解前最好先用symrcm 來排列。這個函式對於對稱或非對稱矩陣都能使用。
對於實數的對稱稀疏矩陣 S 來說, S(r,r) 和 S
的特徵值是一樣的,但是執行 eig(S(r,r)) 所花的時間很可能比 eig(S)還少。
Algorithm
The algorithm first finds a pseudoperipheral vertex of the graph of the matrix. It then generates a level structure by breadth-first search and orders the vertices by decreasing distance from the pseudoperipheral vertex. The implementation is based closely on the SPARSPAK implementation described by George and Liu.
Examples
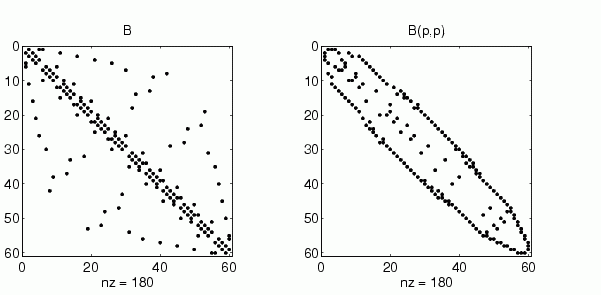
B = bucky
uses an M-file in the demos toolbox to generate the adjacency graph of a truncated icosahedron. This is better known as a soccer ball, a Buckminster Fuller geodesic dome (hence the name bucky), or, more recently, as a 60-atom carbon molecule. There are 60 vertices. The vertices have been ordered by numbering half of them from one hemisphere, pentagon by pentagon; then reflecting into the other hemisphere and gluing the two halves together. With this numbering, the matrix does not have a particularly narrow bandwidth, as the first spy plot shows
subplot(1,2,1), spy(B), title('B')
reverse Cuthill-McKee ordering 可由下列指令求得:
p = symrcm(B); R = B(p,p);
執行 spy 函式可看出非零結構圍成的圖形頻寬(bandwidth)變窄:
subplot(1,2,2), spy(R), title('B(p,p)')
[i,j] = find(B); bw = max(i-j) + 1
See Also
colamd, colmmd, colperm, symamd, symmmd
References
[1] George, Alan and Joseph Liu, Computer Solution of Large Sparse Positive Definite Systems, Prentice-Hall, 1981.
[2] Gilbert, John R., Cleve Moler, and Robert Schreiber, "Sparse Matrices in MATLAB: Design and Implementation," to appear in SIAM Journal on Matrix Analysis, 1992. A slightly expanded version is also available as a technical report from the Xerox Palo Alto Research Center.
 | symmmd | symvar |  |