

| MATLAB Function Reference |   |
Syntax
R = sprandsym(S) R = sprandsym(n,density) R = sprandsym(n,density,rc) R = sprandsym(n,density,rc,kind)
Description
R = sprandsym(S)
回傳一個下三角及對角線和 S 結構相同的對稱亂數矩陣。其元素為平均值 0 及變異數 1 的正規分布(normally distributed)。
R = sprandsym(n,density)
回傳一個 n x n 的對稱亂數稀疏矩陣,其非零元素約有 density*n*n 個 (0 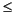
density 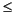
1)。每個非零元素為一個或多個正規分布亂數樣本的總和。
R = sprandsym(n,density,rc)
回傳一個倒數條件數字(reciprocal condition number)為 rc 的矩陣。其元素為非均勻(nonuniform)分布;其為相對於 0 的對稱;其範圍為 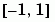 .
.
若 rc 為長度 n 的向量,則 R 的固有值(eigenvalues) 為 rc。因此,如果 rc 是正數向量,則 R 為正定矩陣(positive definite matrix)。在另一種情況,R 是根據所給的固有值或條件數字對一個對角矩陣作 random Jacobi rotations 所產生的。其在拓撲與代數結構的數量非常龐大。
R = sprandsym(n,density,rc,kind)
回傳一個正定矩陣(positive definite matrix)。參數 kind 可為:
1, R 由正定對角矩陣(positive definite diagonal matrix)作 random Jacobi rotation 而產生。 R 正確地擁有其所要的條件數字。2, R 為外積(outer products)的轉移和(shifted sum)。R 只擁有近似的條件數字,但其結構較小。3, R 擁有和矩陣 S 相同的結構及近似條件數字 1/rc。而密度 density 可忽略。See Also
sprand 產生均勻分布(normally distributed)的亂數稀疏矩陣
sprandn 產生正規分布(normally distributed)的亂數稀疏矩陣
 | sprandn | sprintf |  |