rat, rats (MATLAB Function Reference)

Rational fraction approximation

Syntax

[N,D] = rat(X)
[N,D] = rat(X,tol)
rat(...)
S = rats(X,strlen)
S = rats(X)

Description

Even though all floating-point numbers are rational numbers, it is sometimes desirable to approximate them by simple rational numbers, which are fractions whose numerator and denominator are small integers. The rat function attempts to do this. Rational approximations are generated by truncating continued fraction expansions. The rats function calls rat, and returns strings.

[N,D] = rat(X) returns arrays N and D so that N./D approximates X to within the default tolerance, 1.e-6*norm(X(:),1).

[N,D] = rat(X,tol) returns N./D approximating X to within tol.

rat(X), with no output arguments, simply displays the continued fraction.

S = rats(X,strlen) returns a string containing simple rational approximations to the elements of X. Asterisks are used for elements that cannot be printed in the allotted space, but are not negligible compared to the other elements in X. strlen is the length of each string element returned by the rats function. The default is strlen = 13, which allows 6 elements in 78 spaces.

S = rats(X) returns the same results as those printed by MATLAB with format rat.

Examples

Ordinarily, the statement

 s = 1 - 1/2 + 1/3 - 1/4 + 1/5 - 1/6 + 1/7

produces

 s =
    0.7595

However, with

 format rat

or with

 rats(s)

the printed result is

 s = 
    319/420

This is a simple rational number. Its denominator is 420, the least common multiple of the denominators of the terms involved in the original expression. Even though the quantity s is stored internally as a binary floating-point number, the desired rational form can be reconstructed.

To see how the rational approximation is generated, the statement rat(s)

produces

 1 + 1/(-4 + 1/(-6 + 1/(-3 + 1/(-5))))

And the statement

 [n,d] = rat(s)

produces

n = 319, d = 420

The mathematical quantity 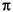is certainly not a rational number, but the MATLAB quantity pi that approximates it is a rational number. pi is the ratio of a large integer and 2⁵²:

 14148475504056880/4503599627370496

However, this is not a simple rational number. The value printed for pi with format rat, or with rats(pi), is

 355/113

This approximation was known in Euclid's time. Its decimal representation is

 3.14159292035398

and so it agrees with pi to seven significant figures. The statement

 rat(pi)

produces

 3 + 1/(7 + 1/(16))

This shows how the 355/113 was obtained. The less accurate, but more familiar approximation 22/7 is obtained from the first two terms of this continued fraction.

Algorithm

The rat(X) function approximates each element of X by a continued fraction of the form:

The d's are obtained by repeatedly picking off the integer part and then taking the reciprocal of the fractional part. The accuracy of the approximation increases exponentially with the number of terms and is worst when
X = sqrt(2). For x = sqrt(2), the error with k terms is about 2.68*(.173)^k, so each additional term increases the accuracy by less than one decimal digit. It takes 21 terms to get full floating-point accuracy.

See Also

format

rank rbbox