

| MATLAB Function Reference |   |
Syntax
[N,D] = rat(X) [N,D] = rat(X,tol) rat(...) S = rats(X,strlen) S = rats(X)
Description
雖然所有的浮點數都是有理數,不過有時候我們會想以更簡單的有理數表達它們,分子和分母都是小整數的分數。rat 函式就是試著做這件事。有理的近似值經由連續的化簡分數產生出來。rats 函數會呼叫 rat 函數,然後回傳一個字串。
[N,D] = rat(X)
N 陣列和 D 陣列使得 N./D 逼近 X 且誤差小於預設值, 1.e-6*norm(X(:),1) 。
[N,D] = rat(X,tol)
N./D 逼近 X 且誤差在 tol 以下。
S = rats(X,strlen)
X 的簡單有理近似值之字串。當配置的空間不夠時,會以星號(*)來表示相較於 X 其他元素不可忽略的元素。 strlen 是每個 rats 函數傳回字串元素的長度。預設值是 strlen = 13 ,在空間是 78 時允許存 6 個元素。
S = rats(X)
format rat 一樣的結果。
Examples
s = 1 - 1/2 + 1/3 - 1/4 + 1/5 - 1/6 + 1/7
s =
0.7595
format rat
rats(s)
s =
319/420
這是一個簡單的有理數。分母是 420 ,原先式子分母的最小公倍數。
即使 s 是以一個二元浮點數存在電腦內部,不過有理式可以被重建。
1 + 1/(-4 + 1/(-6 + 1/(-3 + 1/(-5))))
[n,d] = rat(s)
n = 319, d = 420
數學上的 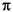 不是一個有理數,但是在 MATLAB 裡,
不是一個有理數,但是在 MATLAB 裡, pi 是一個有理數的近似值。 pi 是一個大整數和 252 的比值:
14148475504056880/4503599627370496
然而,上式不是一個簡單的有理數。以 format rat 或 rats(pi) 計算出來的 pi 是
355/113
這個近似值在歐幾里得的時代就已經被知道了。它的十進位表示法是
3.14159292035398
而這個 pi 值和之前七個字元表示的 pi (355/113)相同。陳述式
rat(pi)
3 + 1/(7 + 1/(16))
它顯示 355/113 是如何得到的,更簡單的近似值 22/7 是從此連續分數的前兩項得到的。
Algorithm
rat(X) 函數經由下面形式的連續分數逼近 X 的每一個元素:

d's 是經由不斷地拿掉整數部份,和取分數部份的倒數得到的。近似值的正確度與分數項的個數成次方增加,而當X = sqrt(2) 時會最差。對於 x = sqrt(2), k 項的誤差大約是 2.68*(.173)^k ,所以每一個增加的項會增加不到十分之一的正確度。它需要 21 項來得到全部的浮點正確度。
See Also
 | rank | rbbox |  |