MATLAB Function Reference

nnls

Nonnegative least squares

Note    The nnls function was replaced by lsqnonneg in Release 11 (MATLAB 5.3). In Release 12 (MATLAB 6.0), nnls displays a warning message and calls lsqnonneg.

Syntax

x = nnls(A,b)
x = nnls(A,b,tol)
[x,w] = nnls(A,b)
[x,w] = nnls(A,b,tol)

Description

x = nnls(A,b) solves the system of equations Ax = b in a least squares sense, subject to the constraint that the solution vector x has nonnegative elements: x_j > 0, j = 1, 2, ... n . The solution x minimizes 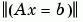subject to x 0.

x = nnls(A,b,tol) solves the system of equations, and specifies a tolerance tol. By default, tol is: max(size(A))*norm(A,1)*eps.

[x,w] = nnls(A,b) also returns the dual vector w, where w_i 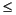0 when x_i = 0 and w_i 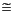0 when x_i > 0.

[x,w] = nnls(A,b,tol) solves the system of equations, returns the dual vector w, and specifies a tolerance tol.

Examples

Compare the unconstrained least squares solution to the nnls solution for a 4-by-2 problem:

A =
    0.0372    0.2869
    0.6861    0.7071
    0.6233    0.6245
    0.6344    0.6170
b =
    0.8587
    0.1781
    0.0747
    0.8405
[A\b nnls(A,b)] =
    -2.5627         0
     3.1108   0.6929

[norm(A*(a\b)-b) norm(A*nnls(a,b)-b)] =
     0.6674 0.9118

The solution from nnls does not fit as well, but has no negative components.

Algorithm

The nnls function uses the algorithm described in [1], Chapter 23. The algorithm starts with a set of possible basis vectors, computes the associated dual vector w, and selects the basis vector corresponding to the maximum value in w to swap out of the basis in exchange for another possible candidate, until w 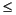0.

See Also

\ Matrix left division (backslash)

References

[1] Lawson, C. L. and R. J. Hanson, Solving Least Squares Problems, Prentice-Hall, 1974, Chapter 23.

nextpow2

nnz