MATLAB Function Reference

del2

離散拉普拉斯(Discrete Laplacian)

Syntax

L = del2(U)
L = del2(U,h)
L = del2(U,hx,hy)
L = del2(U,hx,hy,hz,...)

Definition

如果把矩陣 U 當作一個函數 u(x,y) 在方格點上求得的值， 則 4*del2(U) 是 u 拉普拉斯微分(Laplace's differential)的有限差值近似值，就是：

其中：

在邊緣，同樣的公式應用在三次估計值。

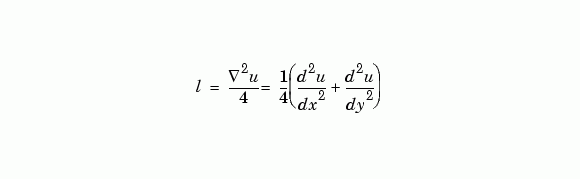
對較多變數的函數 u(x,y,z,...)，del2(U) 是一個近似值，

其中 N 是 u 中變數的數量。

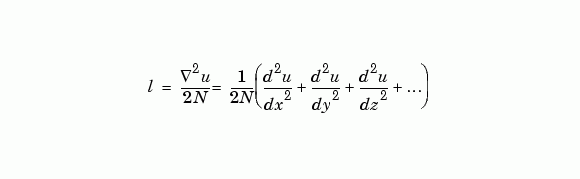
Description

L = del2(U) 是下式的近似值，其中 U 是一個矩形的陣列。

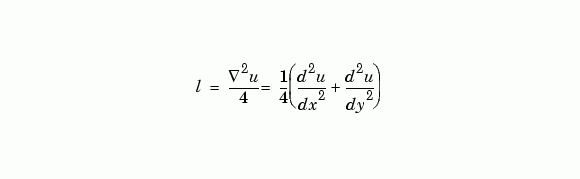
矩陣 L 是和 U 相同大小，而每個元素等於 U 元素間的差值且是它鄰近四個值平均的矩陣。

L = del2(U) 當 U 是一個多維陣列時，傳回下式的近似值

其中 N 是 ndims(u)。

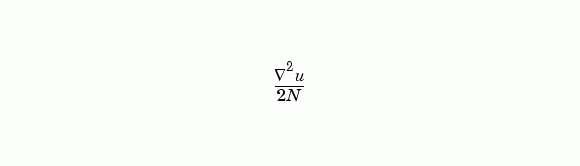
L = del2(U,h) 其中 H 是一個純量，把 H 當作每個維度間距的空間(預設 h=1)。

L = del2(U,hx,hy) 當 U 是一個矩形陣列時，以 hx 和 hy 定義的空間。如果 hx 是純量，那它是代表x-方向的間距。如果 hx 是一個向量，它必須有長度 size(u,2) 且定義點的x-座標。相同地，如果 hy 是一個純量，那它是代表y-方向的間距。如果 hy 是一個向量，它必須有長度 size(u,1) 且定義點的y-座標。

L = del2(U,hx,hy,hz,...) 其中 U 是多維度的，使用以 hx, hy, hz, ... 定義的空間。

Examples

函數

有

對這個函數 4*del2(U) 也是 4 。

[x,y] = meshgrid(-4:4,-3:3);
U = x.*x+y.*y  
U =
    25     18     13     10      9     10     13     18     25
    20     13      8      5      4      5      8     13     20
    17     10      5      2      1      2      5     10     17
    16      9      4      1      0      1      4      9     16
    17     10      5      2      1      2      5     10     17
    20     13      8      5      4      5      8     13     20
    25     18     13     10      9     10     13     18     25

V = 4*del2(U)
V =
     4      4      4      4      4      4      4      4      4
     4      4      4      4      4      4      4      4      4
     4      4      4      4      4      4      4      4      4
     4      4      4      4      4      4      4      4      4
     4      4      4      4      4      4      4      4      4
     4      4      4      4      4      4      4      4      4
     4      4      4      4      4      4      4      4      4

See Also

diff, gradient

default4

delaunay