MATLAB Function Reference

besselj, bessely

Bessel 函數

Syntax

J = besselj(nu,Z)    Bessel function of the 1st kind
Y = bessely(nu,Z)    Bessel function of the 2nd kind
J = besselj(nu,Z,1)
Y = bessely(nu,Z,1)
[J,ierr] = besselj(nu,Z)
[Y,ierr] = bessely(nu,Z)

Definition

微分的等式

被稱為 Bessel's equation，其中 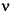是一個實數的常數，而它的解就是 Bessel 函數。

和 對非整數 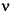形成一個 Bessel's equation 解的基礎集合(fundamental set)。 定義如下：

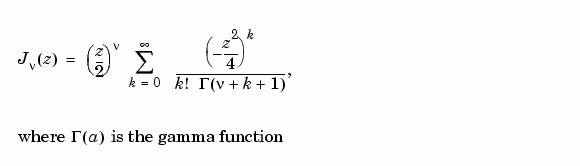
是 Bessel's equation 的第二種解，它跟 是線性獨立(linearly independent)的，定義如下：

Description

J = besselj(nu,Z) 對每個複數陣列 Z 計算第一種 Bessel 函數值 ,。等級 nu 必須不是整數，但必須是整數。參數 Z 可以是複數。當 Z 是正數時結果是實數。

如果 nu 和 Z 是一樣維度的陣列，則結果也是一樣的維度。如果其中之一是單一數值，結果會是另外一個輸入的維度。如果一個輸入參數是一個列(row)向量且另外一個是行(column)向量，結果會是一個二維的函數值表。

Y = bessely(nu,Z) 對非負實數的等級 nu 和參數 Z，計算 第二種 Bessel 函數值。

J = besselj(nu,Z,1) 計算 besselj(nu,Z).*exp(-abs(imag(Z)))。

Y = bessely(nu,Z,1) 計算 bessely(nu,Z).*exp(-abs(imag(Z)))。

[J,ierr] = besselj(nu,Z) 和 [Y,ierr] = bessely(nu,Z) 也傳回錯誤旗標(error flags)的陣列。

ierr = 1	不合法的參數。
ierr = 2	溢位(overflow)。回傳 Inf。
ierr = 3	因化簡而有準確度上的損失。
ierr = 4	不可接受的準確度損失，Z 或 nu 太大。
ierr = 5	沒有收斂(convergence)。 回傳 NaN.

Remarks

Bessel 函數與 Hankel 函數，又稱第三種 Bessel 函數，相關：

其中 是 besselj，而 是 bessely。 Hankel 函數也形成 Bessel's equation 解的基礎集合(fundamental set)(請看 besselh)。

Examples

format long
z = (0:0.2:1)';

besselj(1,z)

ans =
                  0
   0.09950083263924
   0.19602657795532
   0.28670098806392
   0.36884204609417
   0.44005058574493

bessely(1,z)

ans =
               -Inf
  -3.32382498811185
  -1.78087204427005
  -1.26039134717739
  -0.97814417668336
  -0.78121282130029

besselj(3:9,(0:.2:10)') 產生 Abramowitz and Stegun, Handbook of Mathematical Functions 第398頁的整個表。

bessely(3:9,(0:.2:10)') 產生 Abramowitz and Stegun, Handbook of Mathematical Functions 第399頁的表。

Algorithm

besselj 和 bessely 函數用一個 Fortran MEX-file 去呼叫一個由 D. E. Amos [3] [4] 寫的library。

See Also

airy, besseli, besselk

References

[1] Abramowitz, M. and I.A. Stegun, Handbook of Mathematical Functions, National Bureau of Standards, Applied Math. Series #55, Dover Publications, 1965, sections 9.1.1, 9.1.89 and 9.12, formulas 9.1.10 and 9.2.5.

[2] Carrier, Krook, and Pearson, Functions of a Complex Variable: Theory and Technique, Hod Books, 1983, section 5.5.

[3] Amos, D. E., "A Subroutine Package for Bessel Functions of a Complex Argument and Nonnegative Order," Sandia National Laboratory Report, SAND85-1018, May, 1985.

[4] Amos, D. E., "A Portable Package for Bessel Functions of a Complex Argument and Nonnegative Order," Trans. Math. Software, 1986.

besseli, besselk

beta, betainc, betaln