

| 回張智星首頁 │ 回四方書網 │ 至MATLAB專業討論區 │ 至MATLAB專區 |

|

|
| by 張智星 |
| 章節 | 習題數目 |
|---|---|
| 0 | |
| 第01章 MATLAB小傳與外觀 | 4 |
| 第02章 初探MATLAB | 9 |
| 第03章 二維平面繪圖 | 12 |
| 第04章 三維立體繪圖 | 6 |
| 第05章 特殊圖形 | 4 |
| 第06章 影像顯示與讀寫 | 3 |
| 第07章 動畫製作 | 4 |
| 第08章 握把式圖形與GUI設計 | 5 |
| 第09章 GUIDE:GUI設計環境 | 1 |
| 第10章 矩陣的處理與運算 | 5 |
| 第11章 字元與字串 | 3 |
| 第12章 多維陣列 | 2 |
| 第13章 異質陣列 | 8 |
| 第14章 結構陣列 | 3 |
| 第15章 稀疏矩陣 | 1 |
| 第16章 MATLAB的運算元 | 5 |
| 第17章 M檔案 | 5 |
| 第18章 程式流程控制 | 1 |
| 第19章 程式除錯 | 2 |
| 第20章 檔案輸出及輸入 | 2 |
| 第21章 程式計時 | 3 |
| 第22章 程式碼與記憶體之最佳化 | 8 |
| 第23章 應用程式介面 | 4 |
| 第24章 線性代數 | 6 |
| 第25章 多項式的處理與分析 | 4 |
| 第26章 一般數學函數的處理與分析 | 4 |
| 第27章 內插法 | 2 |
| 第28章 曲線擬合與迴歸分析 | 1 |
| 第29章 常微分方程式 | 2 |
| 總數:119 |

 第01章 MATLAB小傳與外觀
第01章 MATLAB小傳與外觀  第02章 初探MATLAB
第02章 初探MATLABy = 0.5*exp(x/3)-x*x*sin(x)其中 x 是函式的輸入,y 是函式的輸出。你的函式必須能夠處理當 x 是純量或是向量的兩種情況。此外,請利用下述兩列程式碼來畫出此函數的圖形:
f(n) = 4*(1 - 1/3 + 1/5 - 1/7 + 1/9 - 1/11 + ...)其中 n 為函式的輸入,級數和 f(n) 則是函式的輸出。
fibo(n+2) = fibo(n+1)+fibo(n)此數列的啟始條件如下:
fibo(1) = 0, fibo(2) = 1.
fibo(n)={[(1+a)/2]^(n-1)-[(1-a)/2]^(n-1)}/a其中 a 是 5 的平方根。寫利用上式一個 MATLAB 的非遞迴函式 fibo2.m 來計算 Fibonacci 數列。
 第03章 二維平面繪圖
第03章 二維平面繪圖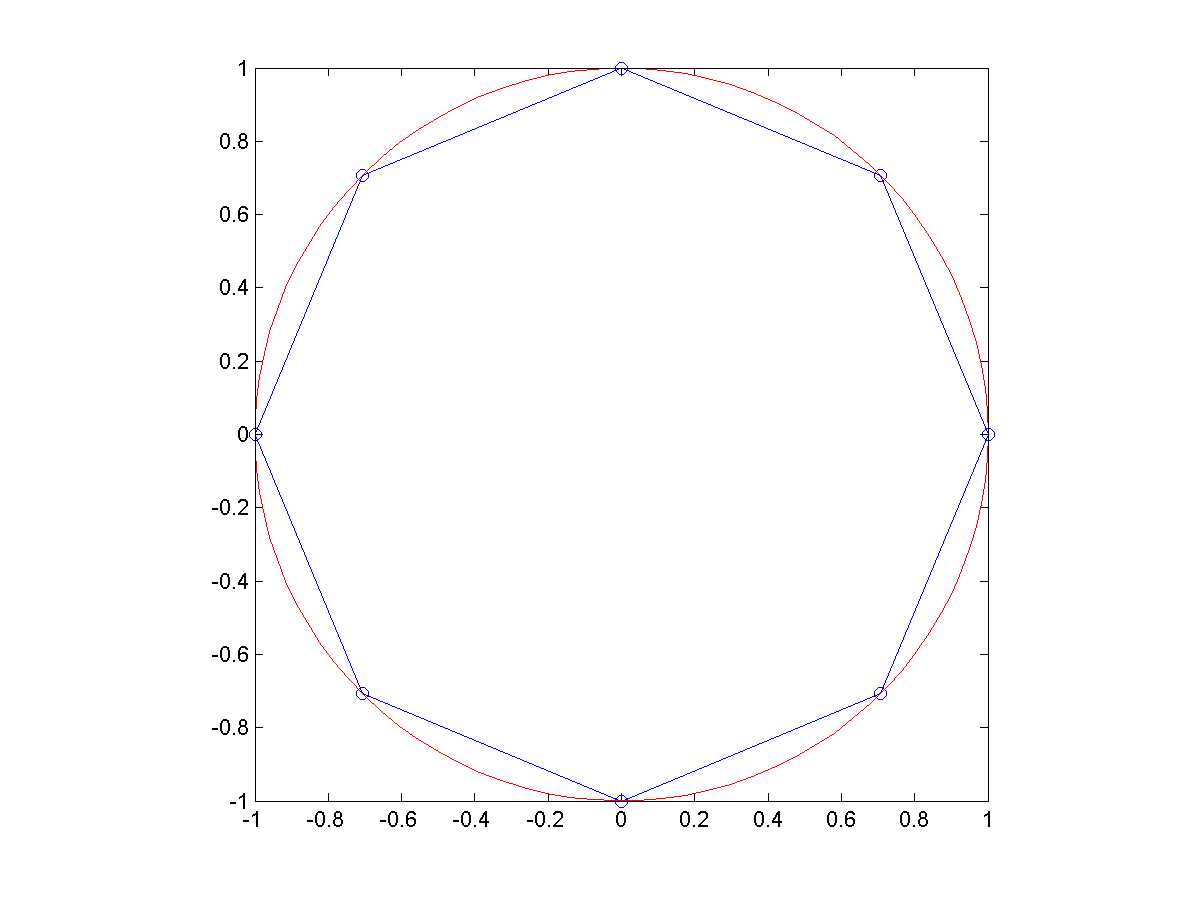
x = sin(t), y = 1 - cos(t) + t/10當 t 由 0 變化到 4*pi 時,請寫一個 MATLAB 的腳本 plotParam.m,畫出此曲線在 XY 平面的軌跡。
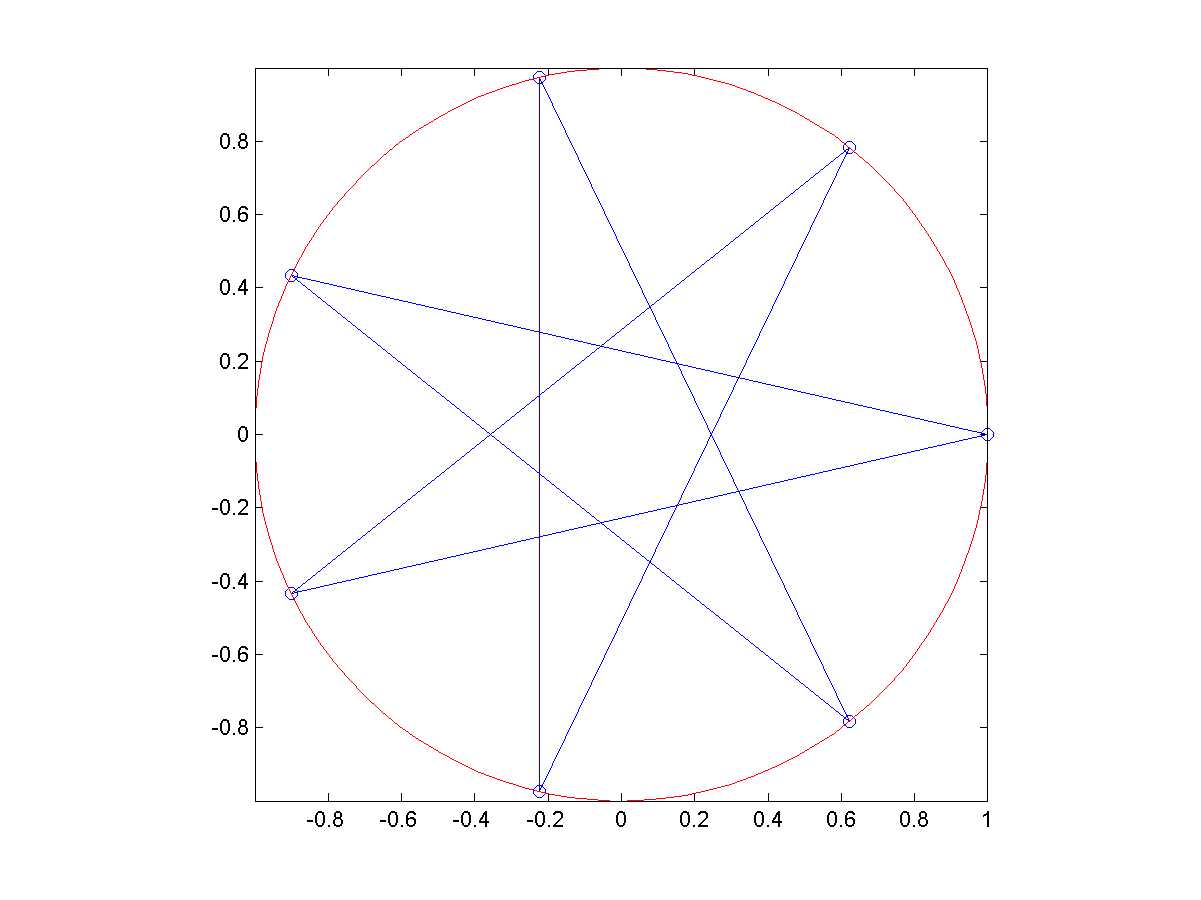
y=cos(m*cos-1(x))其中 x 的值介於 [-1, 1]。當 m 的值由 1 變化到 5,我們可得到五條曲線。請將這五條曲線畫在同一張圖上面,記得要使用 legend 指令來標明每一條曲線。
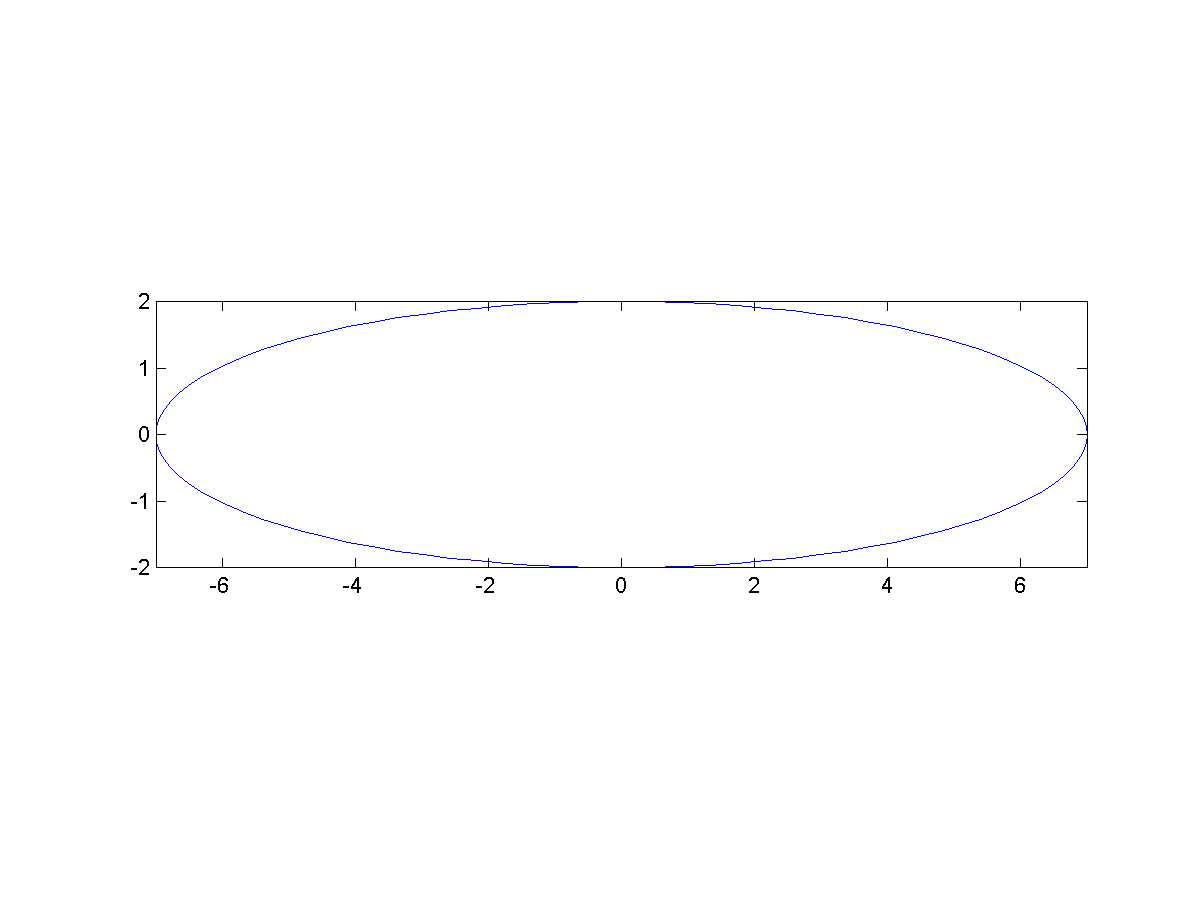
x2+y2=25
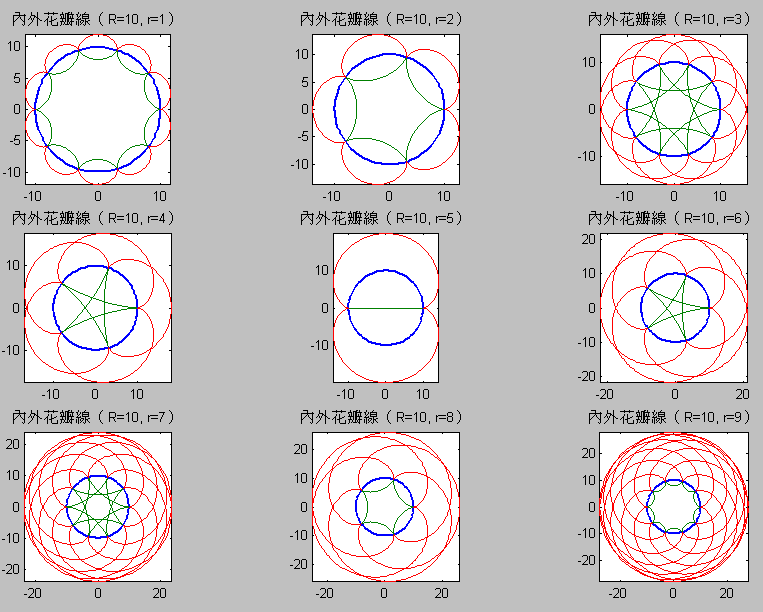
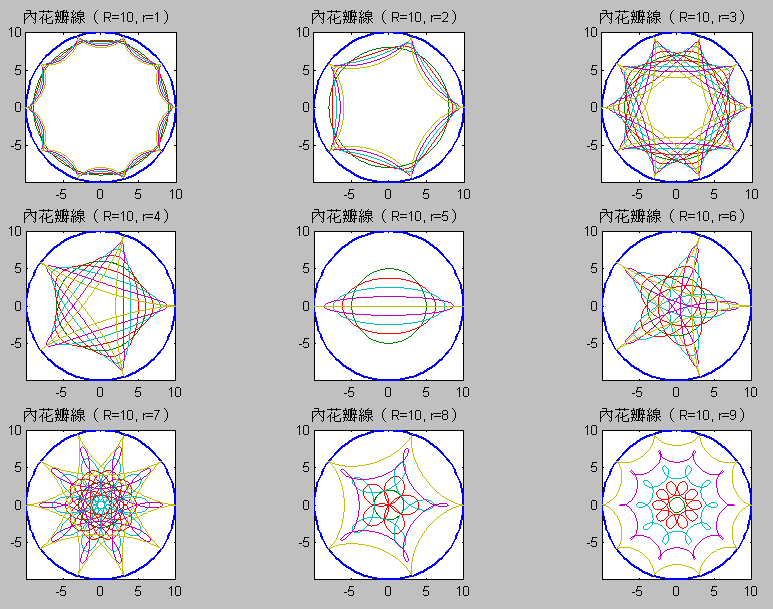
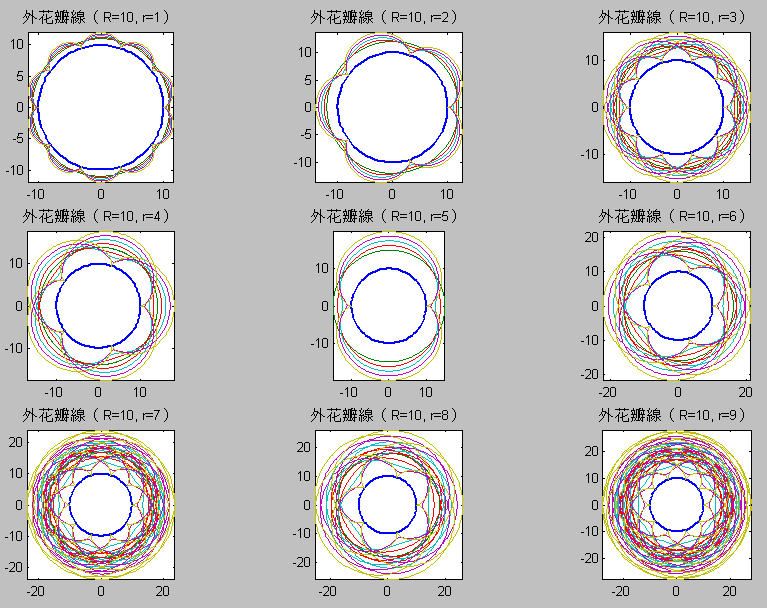
 第04章 三維立體繪圖
第04章 三維立體繪圖 z = sin(x/2)*cos(y)其中,x 的 21 個值均勻分佈在 [-2*pi, 2*pi] 範圍,y 的 31 值均勻分佈在 [-1.5*pi, 1.5*pi]。請使用 subplot(2,1,1) 和 subplot(2,1,2) 將產生的曲面圖和等高線圖秀在同一個視窗上,產生的圖形應類似下圖:
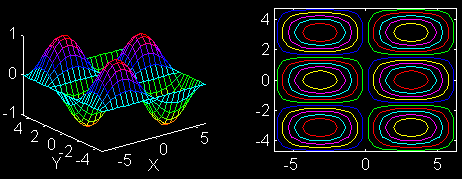
 第05章 特殊圖形
第05章 特殊圖形
| 類別 | |||||||||
| 大一 | 大二 | 大三 | 大四 | 碩一 | 碩二 | 博士班 | 教職員 | ||
| 年份 | 2001 | 10 | 21 | 23 | 14 | 35 | 26 | 47 | 48 |
| 2002 | 21 | 32 | 33 | 24 | 35 | 26 | 17 | 48 | |
| 2003 | 15 | 23 | 23 | 44 | 25 | 34 | 27 | 38 | |
 第06章 影像顯示與讀寫
第06章 影像顯示與讀寫 第07章 動畫製作
第07章 動畫製作 第08章 握把式圖形與GUI設計
第08章 握把式圖形與GUI設計 第09章 GUIDE:GUI設計環境
第09章 GUIDE:GUI設計環境 第10章 矩陣的處理與運算
第10章 矩陣的處理與運算 第11章 字元與字串
第11章 字元與字串以下是Big5的範圍 :
algorithm pseudo-code:
 第12章 多維陣列
第12章 多維陣列資訊系:
| 類別 | ||||||
| 大一新生 | 學士畢業生 | 碩士畢業生 | 博士畢業生 | |||
| 年份 | 2001 | 98 | 94 | 80 | 5 | |
| 2002 | 105 | 97 | 87 | 6 | ||
| 2003 | 121 | 110 | 89 | 8 | ||
電機系:
| 類別 | ||||||
| 大一新生 | 學士畢業生 | 碩士畢業生 | 博士畢業生 | |||
| 年份 | 2001 | 99 | 98 | 85 | 10 | |
| 2002 | 113 | 101 | 87 | 12 | ||
| 2003 | 120 | 115 | 80 | 15 | ||
試用一個 3 維矩陣 A 來表示上述資料。
 第13章 異質陣列
第13章 異質陣列| 張惠妹 | 聽海 | 1998 |
| 周華健 | 花心 | 1992 |
| 王傑 | 一場遊戲一場夢 | 1988 |
| 孫燕姿 | 超快感 | 2000 |
 第14章 結構陣列
第14章 結構陣列| 張惠妹 | 聽海 | 1998 |
| 周華健 | 花心 | 1992 |
| 王傑 | 一場遊戲一場夢 | 1988 |
| 孫燕姿 | 超快感 | 2000 |
試將此異質陣列 A 轉成結構陣列 song,其中:
 第15章 稀疏矩陣
第15章 稀疏矩陣 第16章 MATLAB的運算元
第16章 MATLAB的運算元| 0.3 | 0.1 | 0.2 |
| 0.2 | 0.7 | 0.4 |
| 0.5 | 0.2 | 0.4 |
試找出最小的 n 值使得 An+1=An。此時 An值為何?
 第17章 M檔案
第17章 M檔案 ab ac ad bc bd cd此字串矩陣的每一列代表從輸入字串任取兩個字元時,所有可能的組合。(你的排列順序不見得要和上例完全一樣。)為求簡單起見,我們可假設輸入字串並沒有重複的字元。
abc acb bca bac cab cba此字串矩陣的每一列代表輸入字串所有可能的排列。(你的排列順序不見得要和上例完全一樣。)為求簡單起見,我們可假設輸入字串並沒有重複的字元。
 第18章 程式流程控制
第18章 程式流程控制 第19章 程式除錯
第19章 程式除錯 第20章 檔案輸出及輸入
第20章 檔案輸出及輸入| 1 | 2 | 3 | 4 |
| 5 | 6 | 7 | 8 |
 第21章 程式計時
第21章 程式計時 第22章 程式碼與記憶體之最佳化
第22章 程式碼與記憶體之最佳化[nan 5 3 5 6 3 nan nan 3 4 5 nan 2 nan nan 1 2 3 6]cutshort.m傳回的向量為
[nan 5 3 5 6 3 nan nan nan nan nan nan nan nan nan 1 2 3 6]其中 [3 4 5] 和 [2] 被代換成 [nan nan nan] 及 [nan],因為它們都是「個數小於4、連續的非 nan元素」。如果你的程式碼是完全向量化的(Fully vectorized),將有加分。
 第23章 應用程式介面
第23章 應用程式介面 第24章 線性代數
第24章 線性代數 第25章 多項式的處理與分析
第25章 多項式的處理與分析| 3s2+5s+2 |
| ----------------------- |
| (s+1)3(s2+1) |
 第26章 一般數學函數的處理與分析
第26章 一般數學函數的處理與分析 第27章 內插法
第27章 內插法 第28章 曲線擬合與迴歸分析
第28章 曲線擬合與迴歸分析| x 值 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| y 值 | 2 | 14 | 43 | 90 | 160 | 255 | 378 | 530 | 715 | 930 |
試用下述兩種方法求出參數 a1、a2、b1、b2 的最佳值,並算出最小平方誤差總和。
 第29章 常微分方程式
第29章 常微分方程式| dx1/dt | = | -x2(x3-1) |
| dx2/dt | = | x1(x3-3) |
| dx3/dt | = | x1x2 |
|
您是來自 10.1.40.23 的貴賓,您已光臨本站1次。
(Total page hits: 47,299since August 7, 2000.)
|
|||
|
