[chinese ][all ]
Once we grasp the principle of DP, we can modify DTW for our needs. In this section, we shall introduce another version of DTW with the following characteristics:
Query input: This is a frame-based pitch vector. (For our previous task on pitch labeling, the corresponding time unit for each pitch point is 256/8000 = 1/31.25 = 0.032 s = 32 ms.)
Reference song: This is a note-based pitch vector in which the note duration is discarded for simplicity.
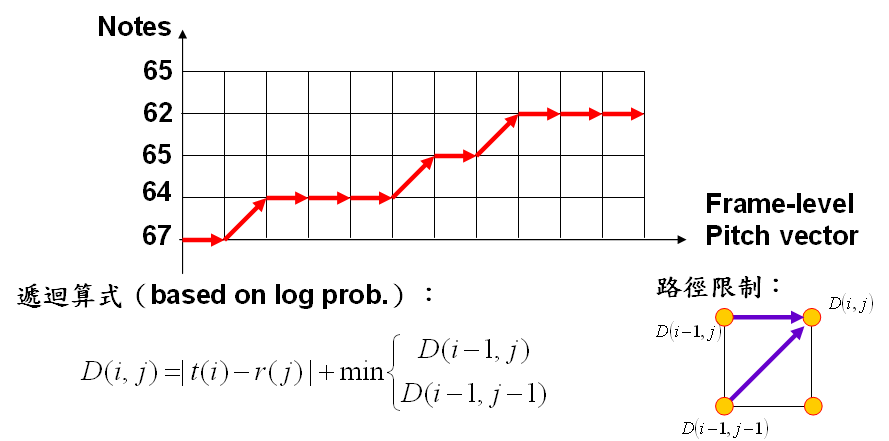
Let t be the input query vector and r be the reference vector. The optimum-value function D(i, j), defined as the minimum distance between t (1:i) and r (1:j), can be expressed in the following recursion:
D(i, j) = min(D(i-1,j), D(i-1, j-1))+|t (i)-r (j)|
Please refer to the following figure:
For simplicity, we shall refer to DTW of this type as type-3 DTW, with the following characteristics:
Type-3 DTW computes the distance between a frame-based pitch vector and a note-based pitch vector. Therefore the computational complexity is lower than those of type-1 and type-2 DTW>
The note duration is not used in the note-based pitch vector for comparison. Hence the recognition rate should not be as good as type-1 and type-2 DTW.
There is no method for one-shot key transposition for type-3 DTW. So we have to rely on trial-and-error method for key transposition.
The following is a typical example of using type-3 DTW for melody alignment:
Example 1: dtw3path01.m pv=[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 47.485736 48.330408 48.917323 49.836778 50.478049 50.807818 50.478049 50.807818 50.478049 49.836778 50.154445 49.836778 50.154445 50.478049 49.524836 0 0 52.930351 52.930351 52.930351 52.558029 52.193545 51.836577 51.836577 51.836577 52.558029 52.558029 52.930351 52.558029 52.193545 51.836577 51.486821 49.218415 48.330408 48.621378 48.917323 49.836778 50.478049 50.478049 50.154445 50.478049 50.807818 50.807818 50.154445 50.154445 50.154445 0 0 0 54.505286 55.349958 55.349958 55.788268 55.788268 55.788268 55.788268 55.788268 55.788268 55.788268 55.788268 55.349958 55.349958 54.505286 54.505286 54.922471 55.788268 55.788268 56.237965 55.788268 55.349958 55.349958 55.349958 55.349958 55.349958 55.349958 55.349958 55.349958 55.349958 55.349958 54.922471 54.922471 54.097918 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 49.218415 49.218415 48.917323 49.218415 49.836778 50.478049 50.478049 50.154445 49.836778 50.154445 49.524836 49.836778 49.524836 0 0 55.788268 53.699915 53.699915 53.310858 53.310858 53.310858 53.310858 52.930351 52.930351 52.930351 52.930351 52.930351 52.558029 52.193545 51.486821 50.154445 49.836778 49.836778 50.154445 50.478049 50.478049 50.154445 49.836778 49.836778 49.524836 49.524836 49.524836 0 0 0 0 56.699654 57.661699 58.163541 58.163541 57.661699 57.661699 57.661699 57.661699 57.661699 57.661699 57.661699 57.661699 58.163541 57.173995 56.699654 56.237965 55.788268 56.237965 56.699654 56.699654 56.237965 55.788268 56.237965 56.237965 56.237965 56.237965 56.237965 56.237965 56.237965 55.788268 54.097918 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 50.154445 50.154445 50.478049 51.143991 51.143991 50.807818 50.154445 51.143991 50.154445 50.478049 50.807818 50.478049 0 0 0 60.330408 61.524836 62.154445 62.807818 62.807818 62.807818 62.807818 62.807818 63.486821 63.486821 63.486821 63.486821 62.807818 62.807818 61.524836 59.213095 58.163541 58.680365 59.213095 59.762739 59.762739 59.762739 59.762739 59.762739 59.762739];
pv(pv==0)=[]; % Delete rests (刪除休止符)
% Note representation, where the time unit of note duration is 1/64 seconds
note=[60 29 60 10 62 38 60 38 65 38 64 77 60 29 60 10 62 38 60 38 67 38 65 77 60 29 60 10 72 38 69 38 65 38 64 38 62 77 0 77 70 29 70 10 69 38 65 38 67 38 65 38];
frameSize=256; overlap=0; fs=8000;
frameRate=fs/(frameSize-overlap);
pv2=note2pv(note, frameRate);
noteMean=mean(pv2(1:length(pv))); % Take the mean of pv2 with the length of pv
pv=pv-mean(pv)+noteMean; % Key transposition
notePitch=note(1:2:end); % Use pitch only (只取音高)
notePitch(notePitch==0)=[]; % Delete rests (刪除休止符)
[minDistance, dtwPath] = dtw3(pv, notePitch, 1, 0);
dtwPathPlot(pv, notePitch, dtwPath);
In the above example, before using type-3 DTW, we have performed the following preprocessing:
Key transposition: We assume the tempo of the query input is the same as the reference song. Therefore we convert the note into frame-based pitch vector for computing the mean value based on the length of the input query. We then shift the input query to have the same mean of the reference song. We can replace this simplified operation by a more precise method for key transposition.
Rest handling: We simply delete all rests in both the input query and the reference song. Again, this is a simplified operation which can be replaced by a more delicate procedure for rest handling.
After the alignment of type-3 DTW in the above example, we can plot the original input PV, shifted PV, and the induced PV, as follows:
Example 2: dtw3inducedPitch01.m pv=[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 47.485736 48.330408 48.917323 49.836778 50.478049 50.807818 50.478049 50.807818 50.478049 49.836778 50.154445 49.836778 50.154445 50.478049 49.524836 0 0 52.930351 52.930351 52.930351 52.558029 52.193545 51.836577 51.836577 51.836577 52.558029 52.558029 52.930351 52.558029 52.193545 51.836577 51.486821 49.218415 48.330408 48.621378 48.917323 49.836778 50.478049 50.478049 50.154445 50.478049 50.807818 50.807818 50.154445 50.154445 50.154445 0 0 0 54.505286 55.349958 55.349958 55.788268 55.788268 55.788268 55.788268 55.788268 55.788268 55.788268 55.788268 55.349958 55.349958 54.505286 54.505286 54.922471 55.788268 55.788268 56.237965 55.788268 55.349958 55.349958 55.349958 55.349958 55.349958 55.349958 55.349958 55.349958 55.349958 55.349958 54.922471 54.922471 54.097918 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 49.218415 49.218415 48.917323 49.218415 49.836778 50.478049 50.478049 50.154445 49.836778 50.154445 49.524836 49.836778 49.524836 0 0 55.788268 53.699915 53.699915 53.310858 53.310858 53.310858 53.310858 52.930351 52.930351 52.930351 52.930351 52.930351 52.558029 52.193545 51.486821 50.154445 49.836778 49.836778 50.154445 50.478049 50.478049 50.154445 49.836778 49.836778 49.524836 49.524836 49.524836 0 0 0 0 56.699654 57.661699 58.163541 58.163541 57.661699 57.661699 57.661699 57.661699 57.661699 57.661699 57.661699 57.661699 58.163541 57.173995 56.699654 56.237965 55.788268 56.237965 56.699654 56.699654 56.237965 55.788268 56.237965 56.237965 56.237965 56.237965 56.237965 56.237965 56.237965 55.788268 54.097918 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 50.154445 50.154445 50.478049 51.143991 51.143991 50.807818 50.154445 51.143991 50.154445 50.478049 50.807818 50.478049 0 0 0 60.330408 61.524836 62.154445 62.807818 62.807818 62.807818 62.807818 62.807818 63.486821 63.486821 63.486821 63.486821 62.807818 62.807818 61.524836 59.213095 58.163541 58.680365 59.213095 59.762739 59.762739 59.762739 59.762739 59.762739 59.762739];
fs=8000; frameRate=fs/256;
%fprintf('Hit return to hear the original pitch vector...\n'); pause; pvPlay(pv, frameRate);
wavwrite(pv2wave(pv, frameRate), fs, 8, 'queryPitchWithRest.wav');
pv(pv==0)=[]; % Delete rests (刪除休止符)
%fprintf('Hit return to hear the pitch vector without rest...\n'); pause; pvPlay(pv, frameRate);
wavwrite(pv2wave(pv, frameRate), fs, 8, 'queryPitchWithoutRest.wav');
origPv=pv;
pvLen=length(origPv);
% Note representation, where the time unit of note duration is 1/64 seconds
note=[60 29 60 10 62 38 60 38 65 38 64 77 60 29 60 10 62 38 60 38 67 38 65 77 60 29 60 10 72 38 69 38 65 38 64 38 62 77 0 77 70 29 70 10 69 38 65 38 67 38 65 38];
pv2=note2pv(note, frameRate);
noteMean=mean(pv2(1:length(pv)));
shiftedPv=pv-mean(pv)+noteMean; % Key transposition
%fprintf('Hit return to hear the shifted pitch vector...\n'); pause; pvPlay(shiftedPv, frameRate);
wavwrite(pv2wave(shiftedPv, frameRate), fs, 8, 'shiftedQueryPitchWithoutRest.wav');
notePitch=note(1:2:end); % Use pitch only (只取音高)
notePitch(notePitch==0)=[]; % Delete rests (刪除休止符)
[minDistance, dtwPath] = dtw3(shiftedPv, notePitch, 1, 0);
inducedPv=notePitch(dtwPath(2,:));
plot(1:pvLen, origPv, '.-', 1:pvLen, shiftedPv, '.-', 1:pvLen, inducedPv, '.-');
legend('Original PV', 'Best shifted PV', 'Induced PV', 4);
fprintf('Min. distance = %f\n', minDistance);
inducedNote=pv2noteStrict(inducedPv, frameRate);
%fprintf('Hit return to hear the induced pitch vector...\n'); pause; notePlay(inducedNote);
wavwrite(note2wave(inducedNote, 1, fs), fs, 8, 'inducedNote.wav'); [�Warning: WAVWRITE will be removed in a future release. Use AUDIOWRITE
instead.]�
[�> In <a href="matlab:matlab.internal.language.introspective.errorDocCallback('wavwrite', 'E:\MATLAB\R2015a\toolbox\matlab\audiovideo\wavwrite.m', 48)" style="font-weight:bold">wavwrite</a> (<a href="matlab: opentoline('E:\MATLAB\R2015a\toolbox\matlab\audiovideo\wavwrite.m',48,0)">line 48</a>)
In <a href="matlab:matlab.internal.language.introspective.errorDocCallback('dtw3inducedPitch01', 'D:\users\jang\books\audioSignalProcessing\example\dtw3inducedPitch01.m', 4)" style="font-weight:bold">dtw3inducedPitch01</a> (<a href="matlab: opentoline('D:\users\jang\books\audioSignalProcessing\example\dtw3inducedPitch01.m',4,0)">line 4</a>)
In <a href="matlab:matlab.internal.language.introspective.errorDocCallback('goWriteOutputFile>dummyFunction', 'D:\users\jang\books\goWriteOutputFile.m', 85)" style="font-weight:bold">goWriteOutputFile>dummyFunction</a> (<a href="matlab: opentoline('D:\users\jang\books\goWriteOutputFile.m',85,0)">line 85</a>)
In <a href="matlab:matlab.internal.language.introspective.errorDocCallback('goWriteOutputFile', 'D:\users\jang\books\goWriteOutputFile.m', 55)" style="font-weight:bold">goWriteOutputFile</a> (<a href="matlab: opentoline('D:\users\jang\books\goWriteOutputFile.m',55,0)">line 55</a>)]�
[�Warning: WAVWRITE will be removed in a future release. Use AUDIOWRITE
instead.]�
[�> In <a href="matlab:matlab.internal.language.introspective.errorDocCallback('wavwrite', 'E:\MATLAB\R2015a\toolbox\matlab\audiovideo\wavwrite.m', 48)" style="font-weight:bold">wavwrite</a> (<a href="matlab: opentoline('E:\MATLAB\R2015a\toolbox\matlab\audiovideo\wavwrite.m',48,0)">line 48</a>)
In <a href="matlab:matlab.internal.language.introspective.errorDocCallback('dtw3inducedPitch01', 'D:\users\jang\books\audioSignalProcessing\example\dtw3inducedPitch01.m', 7)" style="font-weight:bold">dtw3inducedPitch01</a> (<a href="matlab: opentoline('D:\users\jang\books\audioSignalProcessing\example\dtw3inducedPitch01.m',7,0)">line 7</a>)
In <a href="matlab:matlab.internal.language.introspective.errorDocCallback('goWriteOutputFile>dummyFunction', 'D:\users\jang\books\goWriteOutputFile.m', 85)" style="font-weight:bold">goWriteOutputFile>dummyFunction</a> (<a href="matlab: opentoline('D:\users\jang\books\goWriteOutputFile.m',85,0)">line 85</a>)
In <a href="matlab:matlab.internal.language.introspective.errorDocCallback('goWriteOutputFile', 'D:\users\jang\books\goWriteOutputFile.m', 55)" style="font-weight:bold">goWriteOutputFile</a> (<a href="matlab: opentoline('D:\users\jang\books\goWriteOutputFile.m',55,0)">line 55</a>)]�
[�Warning: WAVWRITE will be removed in a future release. Use AUDIOWRITE
instead.]�
[�> In <a href="matlab:matlab.internal.language.introspective.errorDocCallback('wavwrite', 'E:\MATLAB\R2015a\toolbox\matlab\audiovideo\wavwrite.m', 48)" style="font-weight:bold">wavwrite</a> (<a href="matlab: opentoline('E:\MATLAB\R2015a\toolbox\matlab\audiovideo\wavwrite.m',48,0)">line 48</a>)
In <a href="matlab:matlab.internal.language.introspective.errorDocCallback('dtw3inducedPitch01', 'D:\users\jang\books\audioSignalProcessing\example\dtw3inducedPitch01.m', 16)" style="font-weight:bold">dtw3inducedPitch01</a> (<a href="matlab: opentoline('D:\users\jang\books\audioSignalProcessing\example\dtw3inducedPitch01.m',16,0)">line 16</a>)
In <a href="matlab:matlab.internal.language.introspective.errorDocCallback('goWriteOutputFile>dummyFunction', 'D:\users\jang\books\goWriteOutputFile.m', 85)" style="font-weight:bold">goWriteOutputFile>dummyFunction</a> (<a href="matlab: opentoline('D:\users\jang\books\goWriteOutputFile.m',85,0)">line 85</a>)
In <a href="matlab:matlab.internal.language.introspective.errorDocCallback('goWriteOutputFile', 'D:\users\jang\books\goWriteOutputFile.m', 55)" style="font-weight:bold">goWriteOutputFile</a> (<a href="matlab: opentoline('D:\users\jang\books\goWriteOutputFile.m',55,0)">line 55</a>)]�
Min. distance = 204.876547
[�Warning: WAVWRITE will be removed in a future release. Use AUDIOWRITE
instead.]�
[�> In <a href="matlab:matlab.internal.language.introspective.errorDocCallback('wavwrite', 'E:\MATLAB\R2015a\toolbox\matlab\audiovideo\wavwrite.m', 48)" style="font-weight:bold">wavwrite</a> (<a href="matlab: opentoline('E:\MATLAB\R2015a\toolbox\matlab\audiovideo\wavwrite.m',48,0)">line 48</a>)
In <a href="matlab:matlab.internal.language.introspective.errorDocCallback('dtw3inducedPitch01', 'D:\users\jang\books\audioSignalProcessing\example\dtw3inducedPitch01.m', 26)" style="font-weight:bold">dtw3inducedPitch01</a> (<a href="matlab: opentoline('D:\users\jang\books\audioSignalProcessing\example\dtw3inducedPitch01.m',26,0)">line 26</a>)
In <a href="matlab:matlab.internal.language.introspective.errorDocCallback('goWriteOutputFile>dummyFunction', 'D:\users\jang\books\goWriteOutputFile.m', 85)" style="font-weight:bold">goWriteOutputFile>dummyFunction</a> (<a href="matlab: opentoline('D:\users\jang\books\goWriteOutputFile.m',85,0)">line 85</a>)
In <a href="matlab:matlab.internal.language.introspective.errorDocCallback('goWriteOutputFile', 'D:\users\jang\books\goWriteOutputFile.m', 55)" style="font-weight:bold">goWriteOutputFile</a> (<a href="matlab: opentoline('D:\users\jang\books\goWriteOutputFile.m',55,0)">line 55</a>)]�
In the above example, the green line is the original input PV, the green line is the shifted PV, and the red line is the induced PV. Since the discrepancy between the shifted and induced PVs is still too big, we can conclude that the key transposition is satisfactory. It is likely that the tempo of the query input is not close to that of the reference song. The reference song is "Happy Birthday" and we can hear the related files:
If we want to do a better job in the alignment, we need to improve key transposition. A straightforward method is to do a linear (exhaustive) search of 81 comparisons with the range [-2, 2], as shown in the following example:
Example 3: dtw3inducedPitch02.m pv=[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 47.485736 48.330408 48.917323 49.836778 50.478049 50.807818 50.478049 50.807818 50.478049 49.836778 50.154445 49.836778 50.154445 50.478049 49.524836 0 0 52.930351 52.930351 52.930351 52.558029 52.193545 51.836577 51.836577 51.836577 52.558029 52.558029 52.930351 52.558029 52.193545 51.836577 51.486821 49.218415 48.330408 48.621378 48.917323 49.836778 50.478049 50.478049 50.154445 50.478049 50.807818 50.807818 50.154445 50.154445 50.154445 0 0 0 54.505286 55.349958 55.349958 55.788268 55.788268 55.788268 55.788268 55.788268 55.788268 55.788268 55.788268 55.349958 55.349958 54.505286 54.505286 54.922471 55.788268 55.788268 56.237965 55.788268 55.349958 55.349958 55.349958 55.349958 55.349958 55.349958 55.349958 55.349958 55.349958 55.349958 54.922471 54.922471 54.097918 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 49.218415 49.218415 48.917323 49.218415 49.836778 50.478049 50.478049 50.154445 49.836778 50.154445 49.524836 49.836778 49.524836 0 0 55.788268 53.699915 53.699915 53.310858 53.310858 53.310858 53.310858 52.930351 52.930351 52.930351 52.930351 52.930351 52.558029 52.193545 51.486821 50.154445 49.836778 49.836778 50.154445 50.478049 50.478049 50.154445 49.836778 49.836778 49.524836 49.524836 49.524836 0 0 0 0 56.699654 57.661699 58.163541 58.163541 57.661699 57.661699 57.661699 57.661699 57.661699 57.661699 57.661699 57.661699 58.163541 57.173995 56.699654 56.237965 55.788268 56.237965 56.699654 56.699654 56.237965 55.788268 56.237965 56.237965 56.237965 56.237965 56.237965 56.237965 56.237965 55.788268 54.097918 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 50.154445 50.154445 50.478049 51.143991 51.143991 50.807818 50.154445 51.143991 50.154445 50.478049 50.807818 50.478049 0 0 0 60.330408 61.524836 62.154445 62.807818 62.807818 62.807818 62.807818 62.807818 63.486821 63.486821 63.486821 63.486821 62.807818 62.807818 61.524836 59.213095 58.163541 58.680365 59.213095 59.762739 59.762739 59.762739 59.762739 59.762739 59.762739];
pv(pv==0)=[]; % Delete rests (刪除休止符)
origPv=pv;
pvLen=length(origPv);
% Note representation, where the time unit of note duration is 1/64 seconds
note=[60 29 60 10 62 38 60 38 65 38 64 77 60 29 60 10 62 38 60 38 67 38 65 77 60 29 60 10 72 38 69 38 65 38 64 38 62 77 0 77 70 29 70 10 69 38 65 38 67 38 65 38];
frameRate=8000/256;
pv2=note2pv(note, frameRate);
noteMean=mean(pv2(1:length(pv)));
shiftedPv=pv-mean(pv)+noteMean; % Key transposition
notePitch=note(1:2:end); % Use pitch only (只取音高)
notePitch(notePitch==0)=[]; % Delete rests (刪除休止符)
% Linear search of 81 times within [-2 2] (上下平移 81 次,得到最短距離)
clear minDist dtwPath
shift=linspace(-2, 2, 81);
for i=1:length(shift)
newPv=shiftedPv+shift(i);
[minDist(i), dtwPath{i}] = dtw3(newPv, notePitch, 1, 0);
end
[minValue, minIndex]=min(minDist);
bestShift=shift(minIndex);
bestShiftedPv=shiftedPv+bestShift;
inducedPv=notePitch(dtwPath{minIndex}(2,:));
plot(1:pvLen, origPv, '.-', 1:pvLen, bestShiftedPv, '.-', 1:pvLen, inducedPv, '.-');
legend('Original PV', 'Best shifted PV', 'Induced PV', 4);
fprintf('Best shift = %f\n', bestShift);
fprintf('Min. distance = %f\n', minValue);
%fprintf('Hit return to hear the original pitch vector...\n'); pause; pvPlay(origPv, frameRate);
%fprintf('Hit return to hear the shifted pitch vector...\n'); pause; pvPlay(bestShiftedPv, frameRate);
inducedNote=pv2noteStrict(inducedPv, frameRate);
%fprintf('Hit return to hear the induced pitch vector...\n'); pause; notePlay(inducedNote);
fs=16000;
wavwrite(note2wave(inducedNote, 1, fs), fs, 8, 'inducedNote2.wav'); Best shift = 1.300000
Min. distance = 103.332368
[�Warning: WAVWRITE will be removed in a future release. Use AUDIOWRITE
instead.]�
[�> In <a href="matlab:matlab.internal.language.introspective.errorDocCallback('wavwrite', 'E:\MATLAB\R2015a\toolbox\matlab\audiovideo\wavwrite.m', 48)" style="font-weight:bold">wavwrite</a> (<a href="matlab: opentoline('E:\MATLAB\R2015a\toolbox\matlab\audiovideo\wavwrite.m',48,0)">line 48</a>)
In <a href="matlab:matlab.internal.language.introspective.errorDocCallback('dtw3inducedPitch02', 'D:\users\jang\books\audioSignalProcessing\example\dtw3inducedPitch02.m', 34)" style="font-weight:bold">dtw3inducedPitch02</a> (<a href="matlab: opentoline('D:\users\jang\books\audioSignalProcessing\example\dtw3inducedPitch02.m',34,0)">line 34</a>)
In <a href="matlab:matlab.internal.language.introspective.errorDocCallback('goWriteOutputFile>dummyFunction', 'D:\users\jang\books\goWriteOutputFile.m', 85)" style="font-weight:bold">goWriteOutputFile>dummyFunction</a> (<a href="matlab: opentoline('D:\users\jang\books\goWriteOutputFile.m',85,0)">line 85</a>)
In <a href="matlab:matlab.internal.language.introspective.errorDocCallback('goWriteOutputFile', 'D:\users\jang\books\goWriteOutputFile.m', 55)" style="font-weight:bold">goWriteOutputFile</a> (<a href="matlab: opentoline('D:\users\jang\books\goWriteOutputFile.m',55,0)">line 55</a>)]�
Due to a better key transposition, the alignment of type-3 DTW is improved significantly with a much less DTW distance. The related files are shown next:
Hint In general, if we want to perform melody recognition, the exhaustive search for key transposition is impractical due to its excessive computational load. Some heuristic search, such as the binary-like search mentioned in section 2 of this chapter, should be employed instead for such purpose.
In the above example, we can still find some obvious mistake for the alignment. For instance, the fifth induced is too short since it only covers 3 frames. To solve this problem and to improve type-3 DTW in general, we have the following strategies:
Set the range of frame numbers being mapped to each note: For instance, the duration of the frames being mapped to a note should between the range [0.5, 2] of the duration of the note. This can enhance the performance since the duration of each note is used.
Use rests: Except for the leading and trailing rests, any rest in the query input indicates the end of the previous note and the beginning of the next note. We can use this cue for better alignment and query by singing/humming.
We can simply modify our type-3 DTW to meet the above two requirement in order to increase the precision of alignment and the recognition rates of query by singing/humming.
We can employ a modifed version of type-3 DTW which take rests into consideration, as follows:
Example 4: dtw3inducedPitch03.m % ====== Read db
songDb=songDbRead('childSong');
for i=1:length(songDb)
terms=split(songDb(i).songName, '_');
songDb(i).songName=terms{1};
end
% ====== Find the right track
index=find(strcmp('生日快樂', {songDb.songName}));
note=double(songDb(index).track)';
% ====== Pitch tracking
waveFile='happyBirthday.wav';
%waveFile='twinkle_twinkle_little_star.wav';
au=myAudioRead(waveFile);
pfType=1; % 0 for AMDF, 1 for ACF
ptOpt=ptOptSet(au.fs, au.nbits, pfType);
ptOpt.mainFun='maxPickingOverPf';
showPlot=0;
[pv, clarity]=pitchTrack(au, ptOpt, showPlot);
% ====== Compute pv from the given note sequence
index=find(pv~=0); pv=pv(index(1):end); leadingZeroNum=index(1)-1; % Cut off leading zeros
pvNoRest=pv; pvNoRest(pvNoRest==0)=[];
pvLen=length(pv);
pvMean=mean(pvNoRest);
zeroIndex=find(pv==0);
pv(zeroIndex)=nan;
frameRate=au.fs/(ptOpt.frameSize-ptOpt.overlap);
pv2=note2pv(note, frameRate);
noteMean=mean(pv2(1:length(pv)));
shiftedPv=pv-pvMean+noteMean; % Key transposition
notePitch=note(1:2:end); % Use pitch only (只取音高)
notePitch(notePitch==0)=[]; % Delete rests (刪除休止符)
% ====== Linear search of 101 times within [-2 2] (上下平移 101 次,得到最短距離)
clear minDist dtwPath
dtwOpt=dtw3withRestM('defaultOpt');
dtwOpt.endCorner=0;
shift=linspace(-2, 2, 101);
for i=1:length(shift)
newPv=shiftedPv+shift(i);
[minDist(i), dtwPath{i}] = dtw3withRestM(newPv, notePitch, dtwOpt);
end
[minValue, minIndex]=min(minDist);
bestShift=shift(minIndex);
bestShiftedPv=shiftedPv+bestShift;
inducedPv=notePitch(dtwPath{minIndex}(2,:));
inducedPv(zeroIndex)=nan;
% ====== Add back the leading zeros
pv=[nan*ones(1,leadingZeroNum), pv];
bestShiftedPv=[nan*ones(1,leadingZeroNum), bestShiftedPv];
inducedPv=[nan*ones(1,leadingZeroNum), inducedPv];
pvLen=length(pv);
% ====== Plotting and playback
% === Plot the pitch without rest
plot(1:pvLen, pv, '.-', 1:pvLen, bestShiftedPv, '.-', 1:pvLen, inducedPv, '.-');
legend('Original PV', 'Best shifted PV', 'Induced PV', 'location', 'NorthEast');
fprintf('Best shift = %f\n', bestShift);
fprintf('Min. distance = %f\n', minValue);
fprintf('Hit return to hear the original pitch vector...\n'); pause; pvPlay(pv, frameRate);
fprintf('Hit return to hear the shifted pitch vector...\n'); pause; pvPlay(bestShiftedPv, frameRate);
inducedNote=pv2noteStrict(inducedPv, frameRate);
fprintf('Hit return to hear the induced pitch vector...\n'); pause; notePlay(inducedNote, 1);
fs=16000;
%wavwrite(note2wave(inducedNote, 1, fs), fs, 8, 'inducedNote2.wav'); Best shift = 0.880000
Min. distance = 87.066652
Hit return to hear the original pitch vector...
Hit return to hear the shifted pitch vector...
Hit return to hear the induced pitch vector...
Audio Signal Processing and Recognition (音訊處理與辨識)