14-3 Key Transposition (梐)

[english][all]

(請注意：中文版本並未隨英文版本同步更新！)

無論是使用什麼比對方法，我們都必須先進行音調移位（key transposition），例如，男生的歌聲具有較低的key，而女生的歌聲具有較高的key，但歌曲資料庫的音樂卻具有固定的key。因此，對於一段使用者輸入的音高向量（或是進行音符切割後的音符資訊），我們都必須先進行音高的上下平移，以便和資料庫中的歌曲得到最佳的比對。

根據比對方法的不同，音調移位也有不同的作法，可以區分如下：

• 一次到位法：若使用線性伸縮的方法，我們可以使用 median 或是 mean 來直接找出最佳的平移值，因此在計算量較低。（請見後續各小節說明。）
• 試誤法：若使用 type-1 或是 type-2 DTW 等方法，由於無法事先得知最佳的平移值，因此只有採用試誤法（trial and error）來逐次逼近，計算量較大。

若採取試誤法，則我們可以採用任何一種一維函數的最佳化方法，常用的方法有線性搜尋（暴力搜尋）及二元搜尋等兩種方法，可用簡單範例說明如下：

• 
  線性搜尋（暴力搜尋）：
  1. 將輸入音高向量 t 的平均值平移到和標準向量 r（資料庫的歌曲）一樣。（若輸入向量的長度是 m，則標準向量的平均值也是取前 m 個元素來計算。）
  2. 將 t 分別平移到 [-2.0, -1.8, -1.6, ... 1.6, 1.8, 2.0]，並和 r 比對，算出距離的最小值或是相似度的最大值。
• 
  二元搜尋：
  1. 將輸入音高向量 t 的平均值平移到和標準向量 r（資料庫的歌曲）一樣。（若輸入向量的長度是 m，則標準向量的平均值也是取前 m 個元素來計算。）
  2. 設定平移量 s = 2。
  3. 將 t 分別平移到 [-s, 0, s]，和 r 比對，算出距離的最小值或是相似度的最大值，並進行 t 的平移。
  4. 設定 s = s/2，回到前一個步驟，直到收斂。二元搜尋法的示意圖如下：

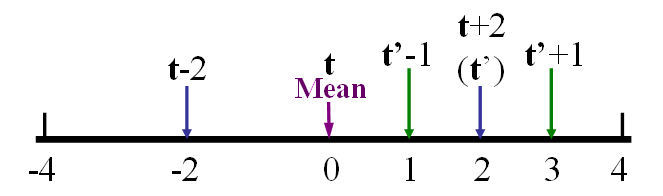
  我們可以使用 Utility Toolbox 裡面的 binSearch4optim 函式來進行上述的二元搜尋。例如，若要搜尋 humps 函數在 [0, 1] 之間的最小值，並限制函數求值（Function Evaluation）的次數是11次，可見下列範例：

  Example 1: binarySearch4min01.m
  objFunction='humps'; % Objective function optimPrm.searchRange=[0.0, 1.0]; optimPrm.evalCount=9; optimPrm.plotOpt=1; [minPair, allPairs]=binarySearch4min(objFunction, optimPrm); fprintf('minX=%f, minY=%f\n', minPair(1), minPair(2)); x=linspace(optimPrm.searchRange(1), optimPrm.searchRange(2), 101); y=humps(x); line(x, y, 'color', 'r'); grid on set(gca, 'ylim', [min(y), max(y)]);minX=0.625000, minY=11.297297
  
  

  在上述範例中，每個紅點代表一次函數求值，紅點旁的數字則是函數求值的順序。

  當然，上述說明只是簡單的範例，讀者可以根據實際需要來調整參數，例如搜尋的範圍以及搜尋的次數等。

  ---

  Audio Signal Processing and Recognition (音訊處理與辨識)