14-3 Key Transposition (梐)

[chinese][english]

(請注意：中文版本並未隨英文版本同步更新！)

Since the query input may have a different key than those used in the song database, we need to perform key transposition before comparison.

無論是使用什麼比對方法，我們都必須先進行音調移位（key transposition），例如，男生的歌聲具有較低的key，而女生的歌聲具有較高的key，但歌曲資料庫的音樂卻具有固定的key。因此，對於一段使用者輸入的音高向量（或是進行音符切割後的音符資訊），我們都必須先進行音高的上下平移，以便和資料庫中的歌曲得到最佳的比對。

Depending on the methods for comparison, we have different schemes for key transposition, as follows:

• One-shot method: If we are using linear scaling, we can simple shift the pitch vector to the mean or median of the database entry to guarantee the distance is minimized. This is very efficient and requires less computation.
• Trial-and-error method: If we are using type-1 or type-2 DTW, we will not be able to know the best amount for key transposition in a one-shot manner. As a result, we need to resort to a certain trial-and-error method to find the best pitch shift amount for key transposition.

根據比對方法的不同，音調移位也有不同的作法，可以區分如下：

• 一次到位法：若使用線性伸縮的方法，我們可以使用 median 或是 mean 來直接找出最佳的平移值，因此在計算量較低。（請見後續各小節說明。）
• 試誤法：若使用 type-1 或是 type-2 DTW 等方法，由於無法事先得知最佳的平移值，因此只有採用試誤法（trial and error）來逐次逼近，計算量較大。

If we are using trial-and-error methods, we can actually adopt any methods for one-dimensional function optimization for such a purpose. Two commonly used methods are explained next. 若採取試誤法，則我們可以採用任何一種一維函數的最佳化方法，常用的方法有線性搜尋（暴力搜尋）及二元搜尋等兩種方法，可用簡單範例說明如下：

• Linear search (exhaustive search):
  1. Shift the mean of the input pitch vector t to the same value of the mean of the song in the database. (If the length of the input vector is m, the mean of the database song should be computed based on the same length too.)
  2. Add each element of [-2.0, -1.8, -1.6, ... 1.6, 1.8, 2.0] to t and compute the minimum distance between t and r.
  
  線性搜尋（暴力搜尋）：
  1. 將輸入音高向量 t 的平均值平移到和標準向量 r（資料庫的歌曲）一樣。（若輸入向量的長度是 m，則標準向量的平均值也是取前 m 個元素來計算。）
  2. 將 t 分別平移到 [-2.0, -1.8, -1.6, ... 1.6, 1.8, 2.0]，並和 r 比對，算出距離的最小值或是相似度的最大值。
• Binary-like search:
  1. Shift the mean of the input pitch vector t to the same value of the mean of the song in the database. (If the length of the input vector is m, the mean of the database song should be computed based on the same length too.)
  2. Set s = 2.
  3. Shift t to each element of [-s, 0, s] and compute the distances to r to find the minimum distance. Shift t according to the minimum distance.
  4. Set s = s/2 and go back to the previous step until it converges. See the following schematic plot for the binary-like search:
  
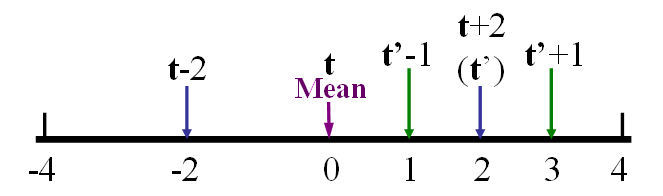
  二元搜尋：
  1. 將輸入音高向量 t 的平均值平移到和標準向量 r（資料庫的歌曲）一樣。（若輸入向量的長度是 m，則標準向量的平均值也是取前 m 個元素來計算。）
  2. 設定平移量 s = 2。
  3. 將 t 分別平移到 [-s, 0, s]，和 r 比對，算出距離的最小值或是相似度的最大值，並進行 t 的平移。
  4. 設定 s = s/2，回到前一個步驟，直到收斂。二元搜尋法的示意圖如下：

  We can use the function binarySearch4min.m in the Utility Toolbox for binary-like search of the minimum of a single-input function. For instance, in the following example, we want to find the minimum of the humps function within [0, 1], and restrict the number of function evaluations to be 9:

  我們可以使用 Utility Toolbox 裡面的 binSearch4optim 函式來進行上述的二元搜尋。例如，若要搜尋 humps 函數在 [0, 1] 之間的最小值，並限制函數求值（Function Evaluation）的次數是11次，可見下列範例：

  Example 1: binarySearch4min01.m
  objFunction='humps'; % Objective function optimPrm.searchRange=[0.0, 1.0]; optimPrm.evalCount=9; optimPrm.plotOpt=1; [minPair, allPairs]=binarySearch4min(objFunction, optimPrm); fprintf('minX=%f, minY=%f\n', minPair(1), minPair(2)); x=linspace(optimPrm.searchRange(1), optimPrm.searchRange(2), 101); y=humps(x); line(x, y, 'color', 'r'); grid on set(gca, 'ylim', [min(y), max(y)]);minX=0.625000, minY=11.297297
  
  

  In the above plot, each red point indicates a function evaluation. The number beside each red dot indicates the sequence in function evaluation. The identified minimum is indicated by a red square.

  在上述範例中，每個紅點代表一次函數求值，紅點旁的數字則是函數求值的順序。

  In practice, for different applications, the user can adjust these parameters, including the search range and the number of function evaluation.

  當然，上述說明只是簡單的範例，讀者可以根據實際需要來調整參數，例如搜尋的範圍以及搜尋的次數等。

  ---

  Audio Signal Processing and Recognition (音訊處理與辨識)