- (*)
中位數的證明:
對於一組已知的純量 {x1, ... xn},請證明此組純量的中位數能夠達到下列目標函數的最小值:
J(u) = S|xi-u| - (*)
平均值的證明:
對於一組已知的純量 {x1, ... xn},請證明此組純量的平均值能夠達到下列目標函數的最小值:
J(u) = S(xi-u)2 - (**)
切音符的函數:
請寫一個能夠執行音符切割的函數 myNoteSegment.m,其使用方法如下:
note = myNoteSegment(pitchVec, timeUnit, pitchTh, minNoteDuration) 其中- pitchVec: 輸入的音高向量
- timeUnit:每一個音高點所對應的時間
- pitchTh:音高差異門檻值,用於切出一個音符
- minNoteDuration:音符的最小長度,以秒為單位。
- note: 切出的音符,以「音高, 音長, 音高, 音長...」的格式來儲存,其中音高的單位是 Semitone,音長的單位是 1/64 秒。
- (**)
LinearScaling的函數:
請寫一個能夠執行線性伸縮的函數 mylinearScaling.m,其使用方法如下:
[minDist, bestVec1, allDist] = myLinearScaling4mr(pitchVec1, pitchVec2, lowerRatio, upperRatio, resolution, distanceType) 其中- pitchVec1: 使用者輸入的音高向量,也是被伸縮及平移的向量
- pitchVec2: 資料庫中的音高向量
- lowerRatio: 最低伸縮比例
- upperRatio: 最高伸縮比例
- resolution: 伸縮總次數
- distanceType: 所用的距離函數,1 代表 L1 norm,2 代表 L2 norm。
- minDist: 線性伸縮的最短距離
- bestVec1: 對應於最短距離、伸縮及平移後的 pitchVec1
- allDist: 線性伸縮的所有距離
- 若 vec1 被拉長後的長度大於 vec2,則不再計算距離。
- 不同的距離計算方式,要進行不同的音高校正。
- 要進行距離的正規化。
- 可以假定輸入的向量不包含休止符。
- 請執行此範例,但將 linScalingMex 改成 myLinearScaling,看看是否得到同樣的效果。
- 請用你的程式碼來測試哼唱選歌的辨識率。
- (***)
editDistance程式碼:
請寫一個 MATLAB 函數 editDistance.m 來實做 Edit Distance,使用格式如下:
[minDist, edPath, edTable] = editDistance(str1, str2) - (***)
DTW3程式碼:
請寫一個 MATLAB 函數 myDtw3.m 來實做 type-3 DTW,使用格式如下:
[minDist, dtwPath, dtwTable] = myDtw3(vec1, vec2) 可由下列半成品進行修改:- 請將此範例內之 dtw3mex 改成 myDtw3,並確認所畫出來的圖形和原範例的圖形一樣。
- 請將你的函數用在最後一題的程式競賽,並只用一次的音高平移,看看辨識率有多高。
- 請將你的函數用在最後一題的程式競賽,並用五次的音高平移(使用二元搜尋法),看看辨識率有多高。
- (***)
DTW3程式碼:改進方案:
請寫一個 MATLAB 函數來重複上一題,但是必須逐次滿足下列三個條件:
- 限制每一個音符所能分配的音框個數:例如每個音符所對應的音框總長度,不得小於音符長度的一半,也不得大於音符長度的兩倍。此規則的加入,使我們可以同時用到音符的音高及音長資訊。
- 使用休止符:在使用者哼唱的音高向量中,除了頭尾的休止符不算外,只要遇到一個休止區間,就代表一個舊音符的結束及新音符的開始,此規則可以適用到一般的哼唱選歌輸入。
- 同時使用上述兩項規則。
- 請將你的函數用在最後一題的程式競賽,並只用一次的音高平移,看看辨識率有多高。
- 請將你的函數用在最後一題的程式競賽,並用五次的音高平移(使用二元搜尋法),看看辨識率有多高。
- (***)
旋律辨識的效能測試之一:
請先閱讀本節的最後一個習題,充分瞭解如何改變參數來進行辨識率的測試後,然後進行下列計算及作圖:
- 使用 LS,請畫出辨識率對辨識時間的作圖,並使用 resolution 為可變參數,使其從 5 增加到 12。畫出的圖應該類似下圖:
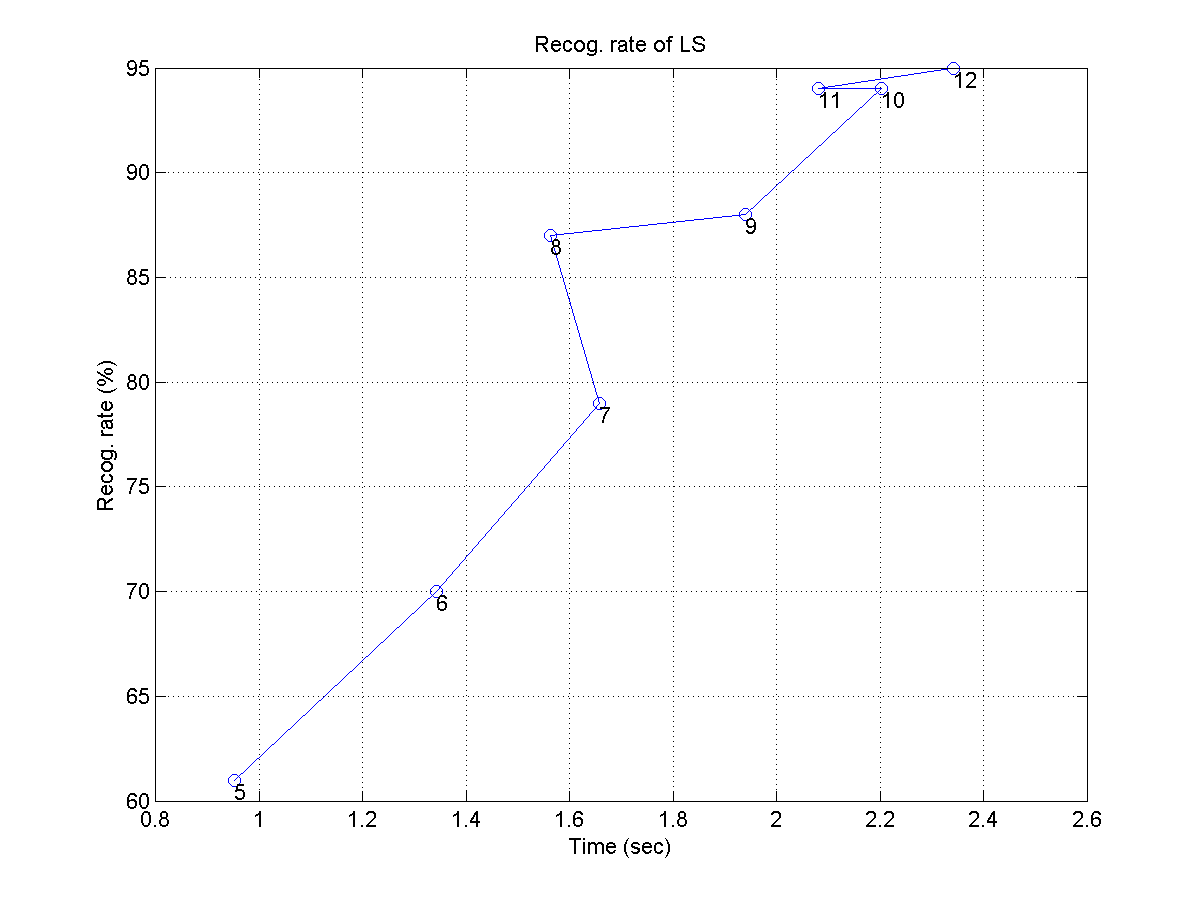
- 使用 type-1 DTW,請畫出辨識率對辨識時間的作圖,並使用二元搜尋法的音調移位次數為可變參數(此參數也是每次比對一首 wav 檔案時,所必須執行 DTW 的個數),請使值為 1, 3, 5, 7, 9。畫出的圖應該類似下圖:
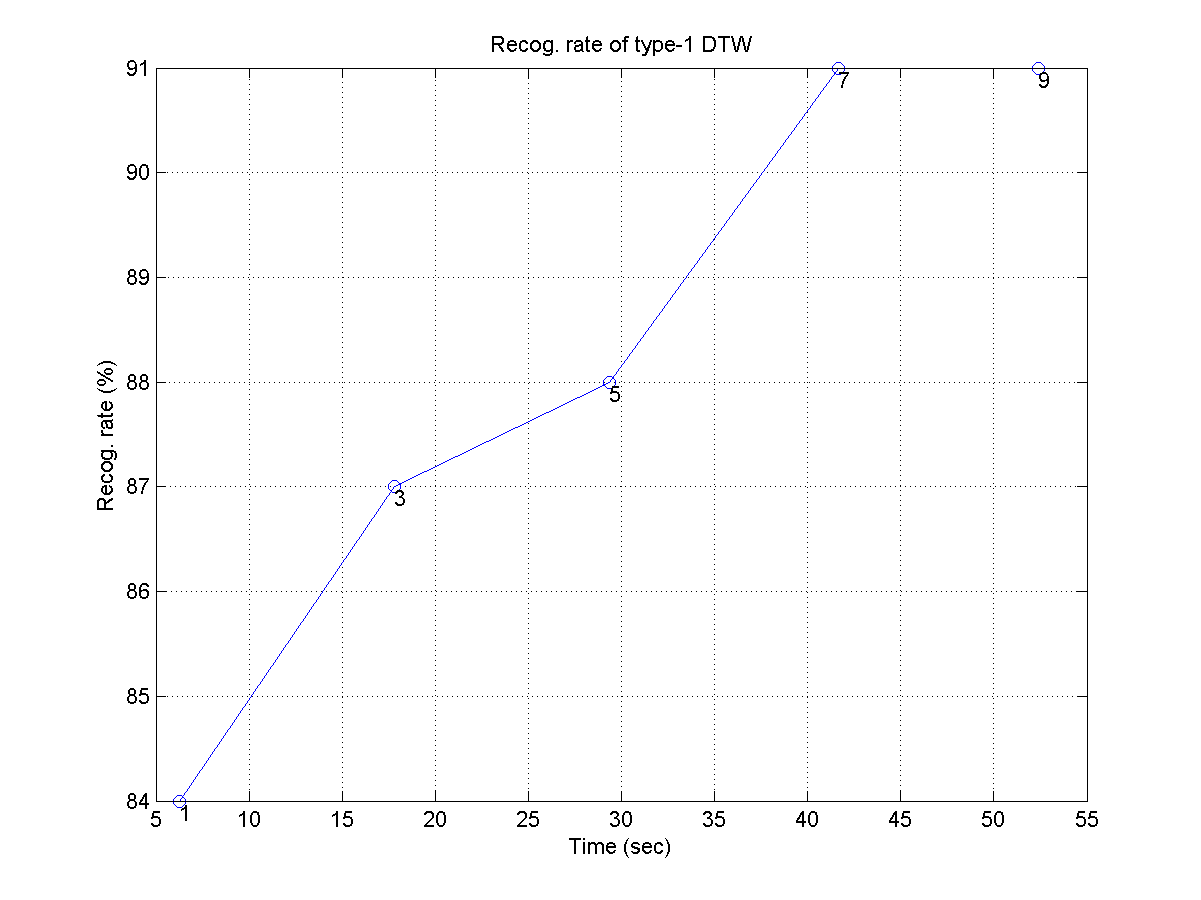
- 請將上述兩圖同時畫出來,以進行 LS 和 DTW 在辨識效能(含辨識率及辨識時間)的比較。由此圖形,你可以得到什麼結論?
- 使用 LS,請畫出辨識率對辨識時間的作圖,並使用 resolution 為可變參數,使其從 5 增加到 12。畫出的圖應該類似下圖:
- (***)
旋律辨識的效能測試之二:
請先閱讀本節的最後一個習題,充分瞭解如何改變參數來進行辨識率的測試後,然後再進行本題。我們標示的音高向量,每一點的持續時間都是 1/31.25 ( = 256/8000) 秒,也就是說,每秒會有 31.25 個音高點。如果旋律辨識的計算時間太長,一個改進的方向,就是逐次降低音高向量在時間軸的解析度,換句話說,如果我們在原始的音高向量中,每 pvrr 點中只取用一點,則每秒的音高解析度降低至 31.25/pvrr 點。本題的目的,即是要探討 pvrr (pitch vector reduction ratio) 對辨識率及辨識時間的影響。請使用四種方法(LS, DTW1, DTW2, DTW3),畫出四條辨識率對辨識時間的曲線,並使用 pvrr 為可變參數。畫出的圖應該類似下圖:
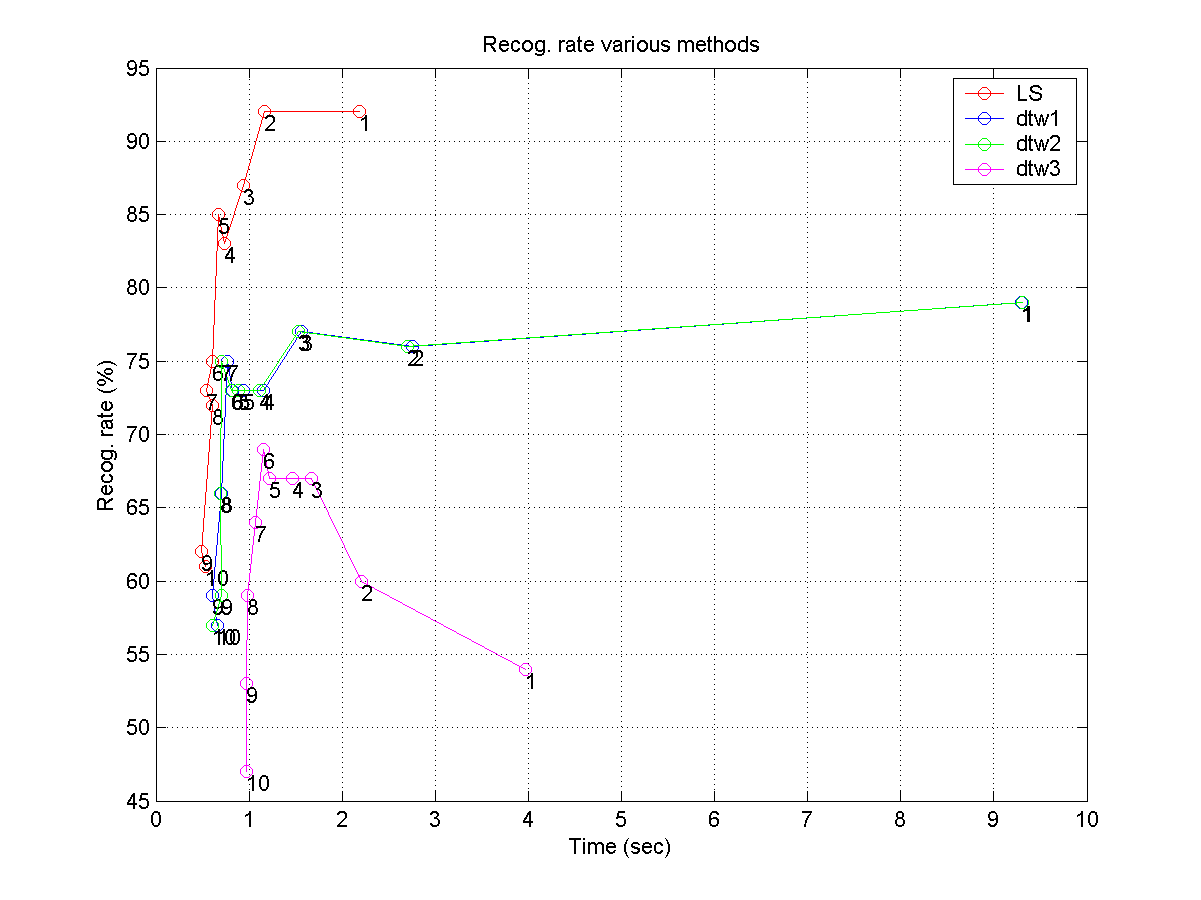
- (***) 程式競賽:使用各種方法進行旋律辨識: 請見此連結。
Audio Signal Processing and Recognition (音訊處理與辨識)
