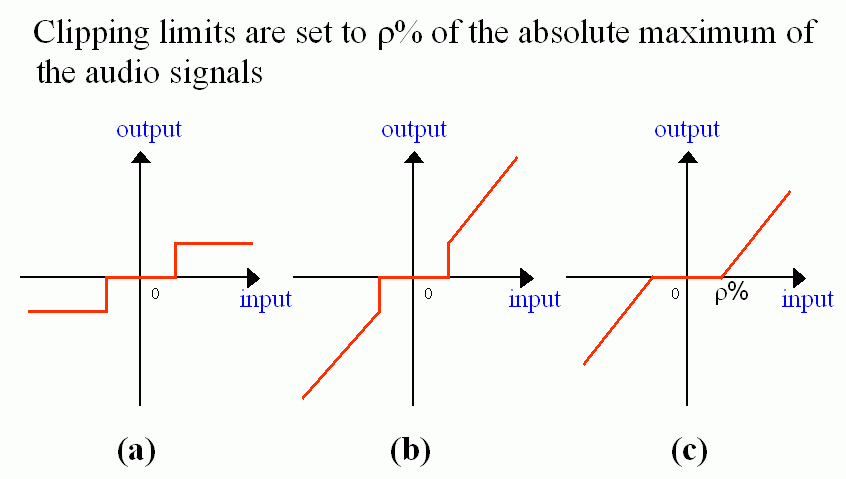Here we shall cover some of the preprocessing techniques that have been proposed to "purify" the signals before pitch tracking. These techniques are seemingly intuitive, but it is still advisable to test these techniques with labeled dataset before using them. These techniques include:
- Pre-filter the signals
- Clip the signals
- SIFT method
Since human's pitch is usually within the range of $[40, 1000]$ Hz, therefore it is a common practice to pass the signals through a low-pass filter in order to remove high-frequency components which are believed to be detrimental to pitch tracking. Usually the cutoff frequency of the low-pass filter is set to 800 to 1000 Hz.
In order to remove noise around zero of the original frame, we can apply center clipping before computing ACF or AMDF. Some of the commonly used techniques for center clipping are displayed in the following figure:
In particular, for pitch tracking over low-end processors (microcontrollers, for instance), it is possible to pass the signal through a binary or ternary sign function such that the further computation of ACF or AMDF can be performed much faster.
在進行音高追蹤之前,有時候我們會將訊號先經過 inverse filtering,企圖找到原先聲帶的原始訊號,這個原始訊號沒有經過口腔、鼻腔的作用,因此理論上會比較乾淨,音高追蹤所得到的效果會比較好,這個方法稱為 SIFT (Simple Inverse Filter Tracking)。
簡單地說,我們是將一個音框中的訊號 $s(i), i=1,\dots,n$ 表示成之前訊號的線性組合: $$s(n) = a_1 s(n-1) + a_2 s(n-2) + \cdots + a_m s(n-m) + e(n)$$ 並利用最小平方法來找出最佳的 $\{a_1, a_2, \dots , a_m\}$,使得 $\sum e^2(n)$ 為最小,此 $s(n)$ 即是所謂的 excitation signal (原始激發訊號),再用此 $s(n)$ 來進行 ACF,得到的效果較好。
在以下的範例中,我們使用一個 m 為 20 的 LPC (linear predictive coefficients) 來進行 SIFT:
由上圖可知,經過了 SIFT,我們使用 residual signal 來進行 ACF,所得到的圖形的高點比較明顯,這會讓我們比較容易找到正確的音高點。
使用 SIFT 加上 ACF 來進行音高追蹤的範例如下:
當遇到雜訊時,基本上是沒有音高存在的,所以 ACF 或是 AMDF 得到的值都是不合理的過低或過高值,因此在實作時,我們必須限定合理的音高範圍,如果超過此範圍,我們就認定沒有音高存在(通常是直接將音高設定為零。)。
有關於音高追蹤的各種其他方法,請見:
Audio Signal Processing and Recognition (音訊處理與辨識)