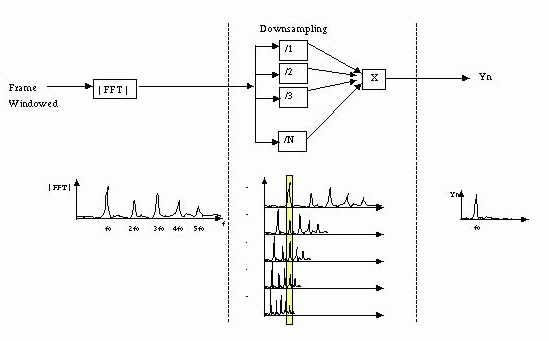
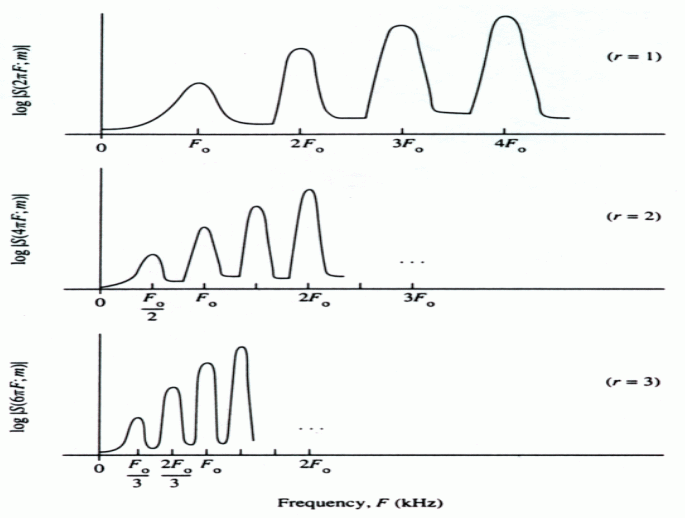
- Harmonic product spectrum (HPS)
- Cepstrum method
以蘇豐文老師的歌聲「soo.wav」為例,如果從第 15000 點開始抓一個 32-ms 的音框(長度為 353 點),以此音框來進行 HPS,結果如下:
In the above plot:
- Subplot 1 is the waveform of the frame.
- Subplot 2 shows the power spectrum and its trend estimated by a 20-order polynomial.
- Subplot 3 shows the trend-subtracted power spectrum and its tapering version.
- Subplot 4 shows the components of HPS, which are of down-sampled versions of tapering power spectrum.
- Subplot 5 shows the HPS and its maximum within a reasonable range for human's pitch.
HPS 的特性說明如下:
- HPS 所得到的音高解析度並不高,以上述範例而言,若不進行補零(Zero Padding),則無論最高點的位置為何,音高都會是 11025/256 = 43.07 Hz z的倍數。若需要提高解析度,我們可以將音框進行補零,此時在頻譜就會有較高的解析度,得到的音高解析度也會提高。在上述範例中,我們進行補零直到音框長度為 16*256 = 4096,所得到的頻率解析度是 fs/4096 = 11025/4096 = 2.69 Hz。
- 因為頻譜容易受到共振峰的影響,所以有時候 HPS 得到的最大值並非對應於正確音高。因此在上述範例中,我們先以多項式來預估頻譜的走勢,再將此走勢從頻譜中扣除(以降低共振峰的影響),同時再讓頻譜值隨頻率變大而漸小(以降低高頻部分的影響),再來進行 HPS,得到的效果比較理想。
Audio Signal Processing and Recognition (音訊處理與辨識)