22-4 蛑q

音訊的辨識有很多應用，除了上述的語音辨識外，我們現在來談談音樂檢索的應用。你是否曾經經歷下列情況：

熟悉的旋律在腦中餘音繞樑、三日不絕，但是卻怎麼也想不起它的歌名。
到 KTV 唱歌，朋友們熟練地從電腦或歌本裡找歌，你卻將歌名、歌手忘光光，而不知該從何找起。

這時候你需要的是「哼唱選歌」（query by singing/humming，簡稱 QBSH），換句話說，你可以哼唱一段主旋律，讓電腦幫你辨識出來這是哪一首歌。這是一個有趣的應用，主要的流程如下：

對使用者的哼唱輸入進行音高追蹤（pitch tracking），以產生隨時間而變的音高向量。
使用前述的音高向量，與資料庫的歌曲進行比對，找出最接近的前十首歌。

首先我們必須瞭解，在講話或唱歌的時候，我們通常倚賴聲門的震動，才能產生週期性的波形（特別是母音），因此聲門的震動頻律就稱為基本頻率，對於整段歌聲，我們希望能夠找到基本頻率隨時間而變的向量（稱為音高向量），根據此向量，我們才能和資料庫中的歌曲進行比對，找出最相似的歌曲。
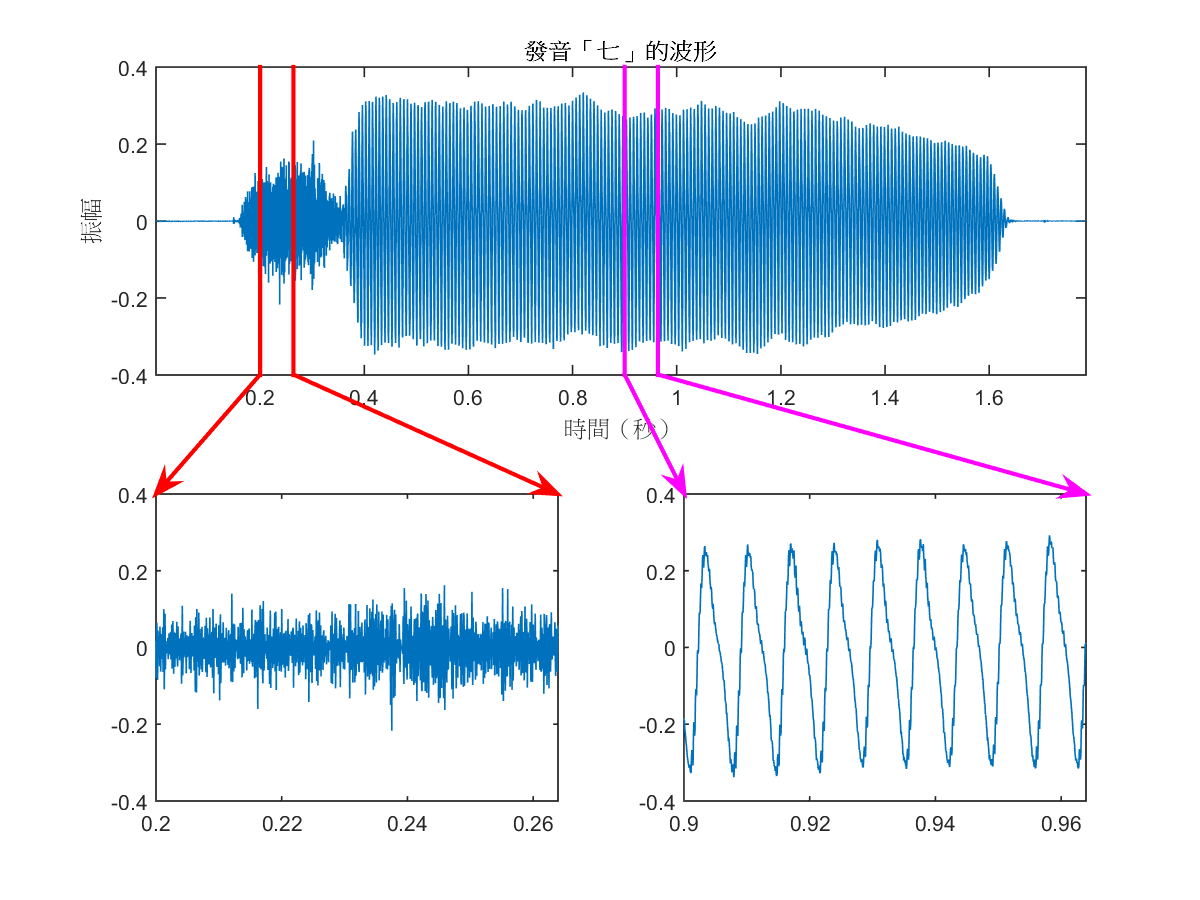
請特別注意，氣音的波形通常沒有規律性，因此也不具有基本頻率。你可以試看看，將你的手按在喉嚨上，並放慢速度說「七」，你可以發覺，在發「ㄑ」時，喉嚨是沒有振動的，聲音完全是由舌頭和牙齒間空氣的急速流動所產生，但在發「ㄧ」時，喉嚨開始進行規律性震動，呈現在外的波形也就有了規律性，請見下列圖例。

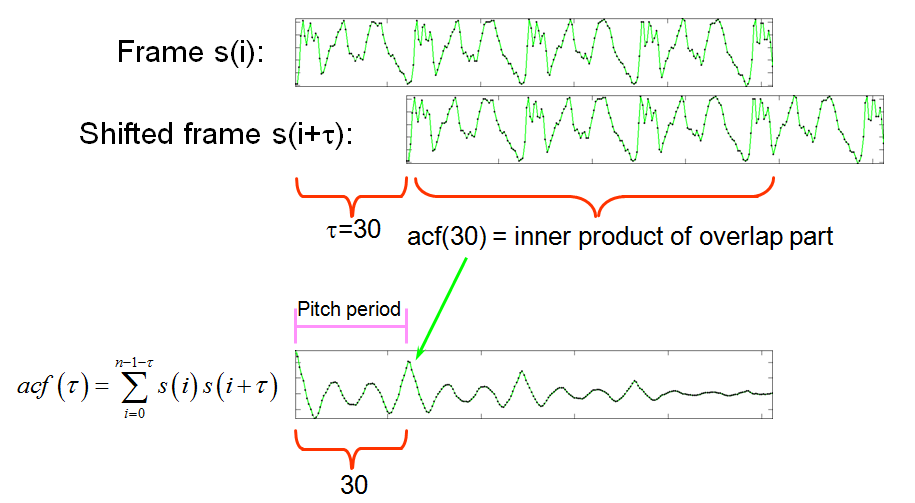
圖 5.：將波形放大後，可以發覺一般子音都沒有週期性，而母音則有明顯的週期性，所以也就有明確的音高。

由上述圖形可以看到，母音有很明顯的規律性，因此我們可以由觀察法來找出基本週期，如同本章第二小節所述，方法並不難，但是若要使用電腦來自動抓音高，就需要一些技術了！這裡有很多方法可以用來抓音高，最直覺的一種方法，稱為自相關函數（audo-correlation function，簡稱 ACF），其原理是對一個音框反覆進行平移及內積，最後算出一條 ACF 曲線，再抓此曲線的第二最大值的位置，此位置的X座標和原點的間隔，即是基本週期（以取樣點為單位），我們再將取樣率除以上述的基本週期，即可得到每秒鐘出現基本週期的次數，這就是音高（以 Hz 為單位，但這和取樣率的 Hz 沒有相關），示意圖如下所示。

圖 5.：使用ACF來計算一個音框的音高。
假設我們使用 $s(i)$ 來代表音框內第 i 個訊號值，那麼 ACF 的公式可以表示如下： $$ acf(\tau)=\sum_{i=0}^{n-1-\tau}s(i)s(i+\tau) $$ 換句話說，將音框每次向右平移一點，和原本音框的重疊部分做內積，重複 n 次後會得到 n 個內積值，這就是 ACF 曲線。當 $\tau=0$ 時，ACF 會有一個最高點，但這不是我們要找的點。當 $\tau$ 慢慢變大時，第一個基本週期會和第二個基本週期疊在一起，此時 ACF 又會出現第二個高點，這個高點就是我們要找的高點，此高點出現的位置，就是我們要找的基本週期。
根據上述的說明，我們就可以對一段聲音訊號進行切音框、計算 ACF、計算音高，並進而找出一段聲音的音高向量，別忘了，靜音是沒有音高的，因此還必須計算每個音框的音量（可簡單定義為每個音框內的訊號平方和），若音量太小，則將此音框的音高設定為零，代表沒有音高。
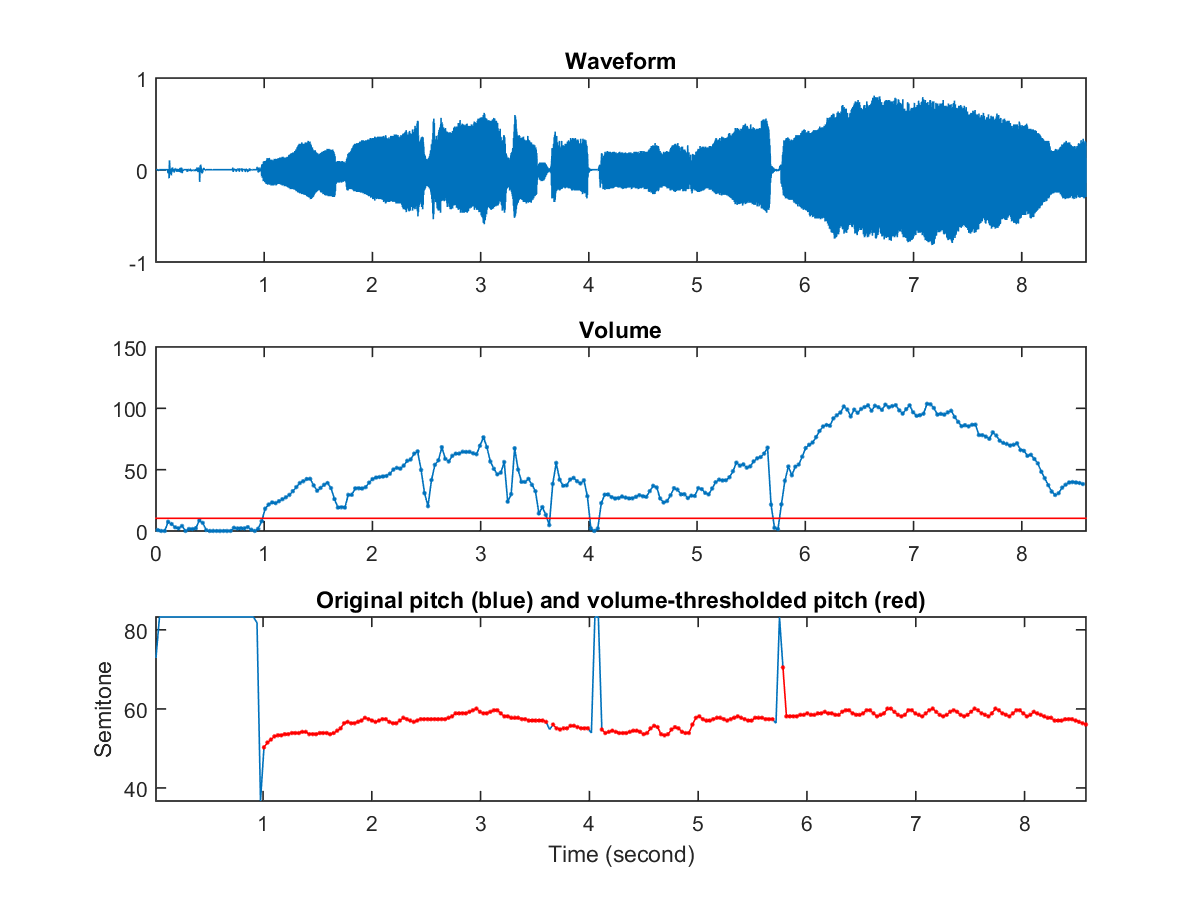
使用上述抓取 ACF 音高點的方法，就可以對一段聲音進行音高追蹤，範例如下：

圖 5.：一段音訊的音高計算，其中小圖一是歌聲波形圖，小圖二是音量曲線（紅色水平線為音量門檻值），小圖三則是音高曲線。
在上圖中共有三個小圖，說明如下：

第一個小圖是原始歌聲波形，內容是「在那遙遠的地方」。
第二個小圖是音量圖，其中的紅線是音量門檻值（等於最大音量的 1/10），若音量低於此門檻值，音高則設定為零。
第三個小圖則是使用 ACF 所算出來的音高曲線。這一段歌聲是由清華大學資工系蘇豐文老師所唱，他曾經是台大合唱團高音部，唱歌技巧很好，所以在整段歌聲的後半部有很明顯的抖音，這個現象也翔實地呈現在對應的音高和音量曲線。

一旦找到音高曲線後，我們要和資料庫中的歌曲進行比對。當然，資料庫的每一首歌曲也都是事先轉成音高向量的形式，通常我們取的音框長度是 32 ms，因此每秒鐘會有 1/32 = 31.25 個音高點，若一首歌有 3 分鐘，對應的音高向量就會有 3*60*31.25 = 5625 點。而我們的哼唱輸入歌聲，若以 8 秒為例，則會產生 8*31.25 = 250 個音高值，我們的目標，就是要找出在這 5625 個點裡面，哪一段最像我們唱出來的 250 個音高值。
其實，當我們說「最像」時，這是一個模糊的概念，所謂「像」或「不像」，完全根據於我們所用到的距離函數，距離越小則越像，反之，則越不像。在計算兩段音高向量的距離時，我們必須考慮到下列問題：

每個人唱歌的音高基準不一樣，例如女生唱歌的key會比較高，而男生會比較低。
每個人唱歌的速度也不一樣，有的人快一些，有的人慢一些，可能都會和資料庫中的歌曲速度不同。
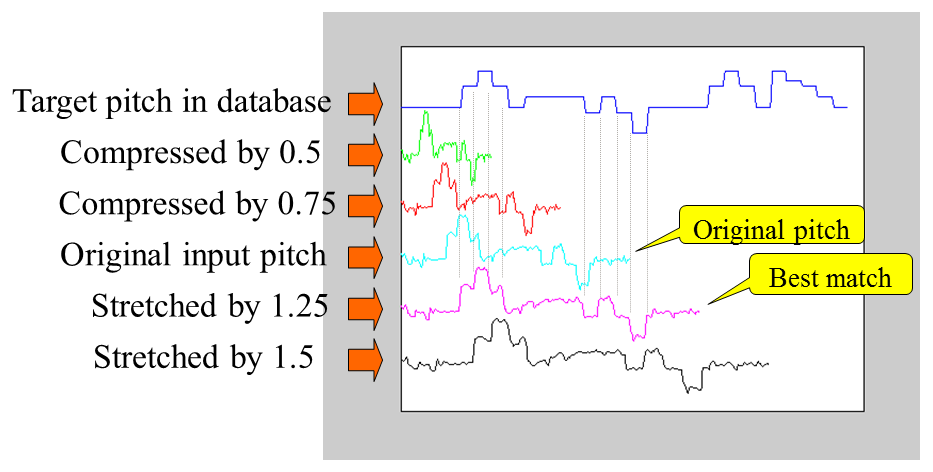
對於第一個問題，我們可以先將兩段音高都平移到同一個音高基準，再進行比對。對於第二個問題，我們可以先假設速度的變化是均勻的（若速度快，就從頭快到尾；若慢，就從頭慢到尾，而不會忽快忽慢），在此情況下，我們就可以採用「線性伸縮」（linear scaling，簡稱 LS）的方法來進行比對，如下圖所示：

圖 5.：使用 LS 來計算歌聲音高和資料庫內的歌曲音高的距離，以本例而言，當伸縮比是 1.25 時，可以得到最短距離。

由上圖中可以看出，當我們將輸入音高向量拉長 1.25 倍（同時將輸入音高向量的平均值平移到對應歌曲音高向量的平均值），將和資料庫中的某一首歌曲得到最近的距離，此距離即是此輸入音高向量和此歌曲的距離。（在此的距離函數可以簡單地定義為兩個向量在高度空間的直線距離。）因此在比對一首歌曲時，我們可以嘗試不同的伸縮倍數，例如從 0.5、0.51、0.52、...、1.49、1.50 等，共 101 種可能，來找出最佳的伸縮倍數以及對應的最短距離。若資料庫中有 1000 首歌曲，將得到 1000 個最短距離，我們可根據這些距離來排序，距離越短的歌曲，就越可能是我們哼唱的歌。
Hint
如果你唱歌忽快忽慢，這時候就不能使用 LS，而要使用運算量更大的 DTW（dynamic time warping）方法來進行比對。

說明至此，我相信大家對哼唱選歌已經有一個基本的瞭解，或許你們會問，那下一步是什麼？還有什麼技術問題尚待克服？其實問題還很多，相關的研究也一直在進行當中，以下列出幾點：

歌曲資料庫的建置，是最大的問題。例如，當我們要將哼唱選歌用於卡拉OK，我們必須先將所有的卡拉OK歌曲建入資料庫，但是如何對這些複音音訊音樂（polyphonic audio music）進行音高追蹤呢？這是一個困難的問題，因為一旦音樂中包含人聲及背景音樂，人聲的音高就很難被準確地計算出來。
第二個問題，哼唱選歌的計算量會隨著資料庫歌曲的提升而增加，雖然增加幅度是小於線性成長，但是若考慮全世界所有的歌曲（超過五億首，且還在持續增加中），運算量是相當驚人。要對付這麼大量的計算，目前最流行的方法是雲端計算（cloud computing），讓大量的 CPU 能夠發揮螞蟻雄兵的功能來完成大量的比對。另一種方式則是採用 GPU (graphic processing unit) 來進行大量的平行運算，我們測試的結果，若要對付 13,000 首歌，從每一個音符起點開始比對，具有 384 核心的 GPU 只要花 3 秒的時間就可以完成 8 秒的哼唱比對，比一般的 CPU 快了將近 20 倍。

關於第一個困難點，你可能會問：但是人耳都聽得出來 MP3 音樂內人聲的音高啊，為什麼電腦做不到？呵呵，這是一個大哉問，我們還不是很明確地知道人腦如何做這件事，但我們明確地知道電腦這件事做不好。每年有一個世界知名的研討會 International Society of Music Information Retrieval（簡稱 ISMIR）會舉辦各項音樂檢索評比，其中有一項是 audio melody extraction，雖然每年的效能都有增加，但目前的 raw pitch accuracy 還不到 85%，可見人耳和人腦在目前的確比電腦厲害很多。當然啦，電腦一直在進步，而人腦進步的幅度有限，「電腦耳」追上「人耳」可能只是時間的問題！
作業

請從網路上尋找任一個展示網頁，來嘗試哼唱選歌的展示系統。

請正常地唱一首歌的其中一句，請問展示系統可以找到你唱的歌嗎？
如果你在唱歌時忽快忽慢，系統還能正確找歌嗎？

Audio Signal Processing and Recognition (音訊處理與辨識)