Chapter 11: Exercises

  1. (**) Use filters to obtain pure-tone signals: Write a MATLAB script to separate a mixed signal of 3 pure-tone components, as follows.
    1. Load the audio file mixSinusoid.wav which is composed of three pure-tone signals with some noise. Can you identify the pitch of these three pure-tone signals by aural perception?
    2. Use fftOneSide.m to plot the one-side magnitude spectrum with respect to frequency. What are the frequencies of these three components?
    3. Use three Butterworth filters (low-pass, band-pass, and hig-hpass) to recover these three components. What is the cutoff frequency you used for designing each filter? Plot these three components for the first 1000 points.
    4. Play these three signals to see if you can hear pure tone. Add these three signals together and play it to see if you can resynthesize the original signal.
  2. (**) DTMF decoding: Write a MATLAB script to decode a DTMF (dual-tone multi-frequency) recording, as follows.
    1. Read the description about DTMF. And here is a typical clip of DTMF: dtmfExample.wav. (Can you identify the corresponding digits by hearing the clip?)
    2. Use any of the endpoint detection methods to segment the recordings. Display the plot to TA to make sure your result is correct. Your plot should be similar to the following one.
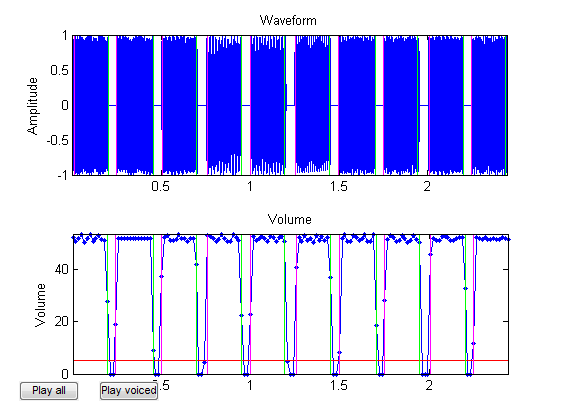
      (Hint: You can use epdByVol.m in SAP toolbox.)
    3. For each of the segments, perform the following steps to identify the corresponding digit:
      • Use Butterworth filters to find the output signals around low-frequency bands (centered around 697 Hz, 770 Hz, 852 Hz, 941 Hz) and high-frequency bands (centered around 1209 Hz, 1336 Hz, 1477 Hz). Plot 8 different output signals and identify the two with the maximum energy. You plot for a segment should be similar to the following one:
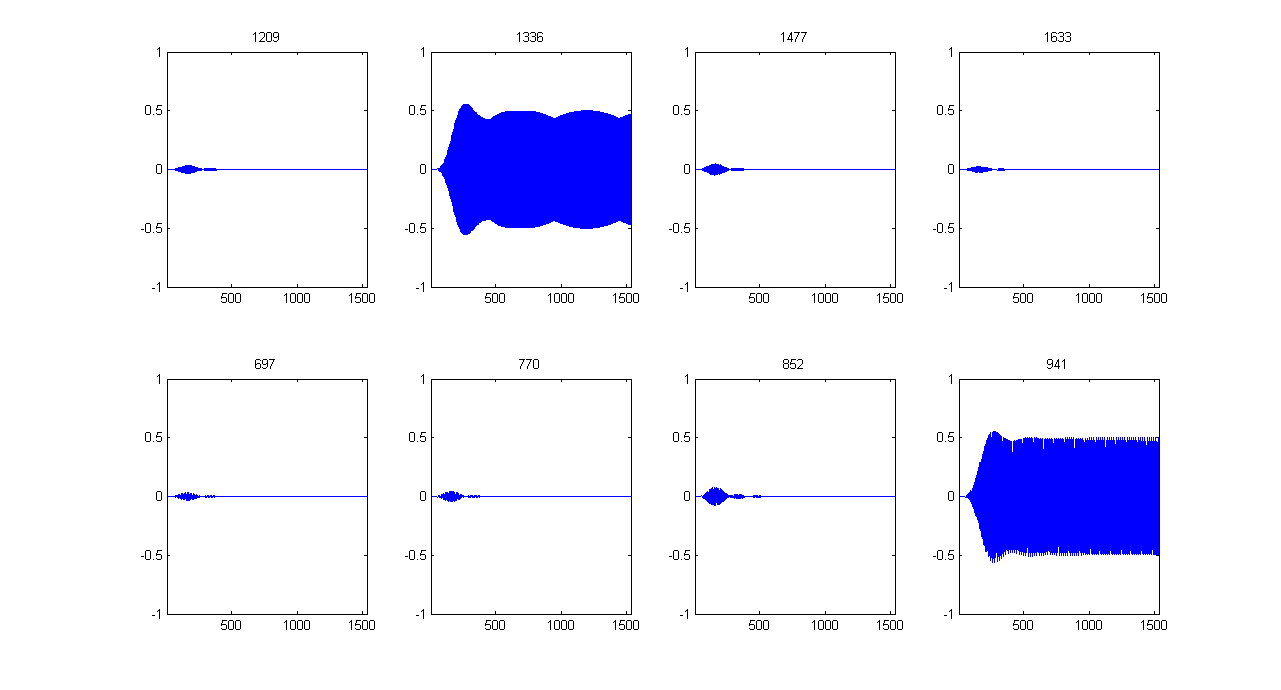
      • Identify the corresponding digit based on the above results.
  3. (**) Human vocal remover: It is known that the pitch of a human is between [40, 1000] Hz or so. Can you design a filter to remove the lead vocal from a polyphonic audio music? Please try this technique over Lady Gaga's "Bad Romance" and see how good it can get. What is the corresponding band-stop frequencies that can achieve the best performance?
Audio Signal Processing and Recognition (音訊處理與辨識)