The loudness of audio signals is the most prominent features according to human aural perception. In general, there are several interchangeable terms that are commonly used to describe the loudness of audio signals, including volume, energy, and intensity. For consistency, here we shall use the term "volume" for describing the loudness. Basically, volume is an acoustic feature that is correlated to the samples' amplitudes within a frame. To define volume quantitatively, we can employ two methods to compute the volume of a given frame:
- The sum of absolute samples within each frame: $$ volume = \sum_{i=1}^n |s_i| $$ where $s_i$ is the $i$-th sample within a frame, and $n$ is the frame size. This method requires only integer operations and it is suitable for low-end platforms such as micro-controllers.
- 10 times the 10-based logarithm of the sum of sample squares:
$$
volume = 10*log_{10} \sum_{i=1}^n s_i^2
$$
This method requires floating-point computations, but it is (more or less) linearly correlated to our perception of loudness of audio signals. The quantity computed is also referred as the "log energy" in the unit of decibels. More explanations about decibels can be found in the following page:
http://www.phys.unsw.edu.au/~jw/dB.html (local copy)
「音量」代表聲音的強度,又稱為「力度」、「強度」(Intensity)或「能量」(Energy),可由一個音框內的訊號震幅大小來類比,基本上兩種方式來計算:
- 每個音框的絕對值的總和:
volume = Si=1n |si| 其中 si 是一個音框中的第 i 個取樣點,而 n 則是每個音框的點數。這種方法的計算較簡單,只需要整數運算,適合用於低階平台(如微電腦等)。 - 每個音框的平方值的總和,再取以 10 為底對數值,再乘以10:
volume = 10*log10(Si=1n si2) 這種方法得到的值是以分貝(Decibels)為單位,是一個相對強度的值,比較符合人耳對於大小聲音的感覺。以下網頁有對分貝的詳細說明:http://www.phys.unsw.edu.au/~jw/dB.html (local copy)
Some characteristics of volume are summarized next.
- For recording in a common quiet office using a uni-directional microphone, the volume of voiced sounds is usually larger than that of unvoiced sounds, and the volume of unvoiced sounds is usually larger than that of environmental noise. (However, this is not applicable to recordings via the omni-directional microphone.)
- Volume is greatly influenced by microphone setups, mostly the microphone gain.
- Volume is usually used for endpoint detection which tries to find the region of meaningful voice activity.
- Before computing the volume, we usually perform zero-justification (by simply subtracting the mean or median of the frame from each samples) to avoid potential DC-bias, as follows.
- For method of "abs sum", we usually apply median subtraction for zero justification.
- For method of "log squared sum", we usually apply mean subtraction for zero justification.
音量具有下列特性:
- 一般而言,有聲音的音量大於氣音的音量,而氣音的音量又大於雜訊的音量。
- 是一個相對性的指標,受到麥克風設定的影響很大。
- 通常用在端點偵測,估測有聲之音母或韻母的開始位置及結束位置。
- 在計算前最好先減去音訊訊號的平均值,以避免訊號的直流偏移(DC Bias)所導致的誤差。
The following example demonstrates how to use these two methods for volume computation:
以下顯示如何以兩種方法來計算音量:
Since we need to compute the volume in many different applications, so we have created a function "frame2volume" (in SAP toolbox) which can compute the volume from a given frame. So we can use the function to simply the previous example:
To go one step further, we can use the function "wave2volume" (in SAP toolbox) which computes volume from a given wave file:
The above two methods of computing volume are only an approximation to our perception of loudness. However, the loudness is based on our perception and there could be significant differences between the "computed loudness" and the "perceived loudness". In fact, the perceived loudness is greatly affected by the freqency as well as the timber of the audio signals. If we plot the equal perceived loudness against sinusoidal signals of varied frequencies, we will have the following curves of equal loudness:
基本上我們使用音量來表示聲音的強弱,但是前述兩種計算音量的方法,只是用數學的公式來逼近人耳的感覺,和人耳的感覺有時候會有相當大的落差,為了區分,我們使用「主觀音量」來表示人耳所聽到的音量大小。例如,人耳對於同樣振福但不同頻率的聲音,所產生的主觀音量就會非常不一樣。若把以人耳為測試主體的「等主觀音量曲線」(Curves of Equal Loudness)畫出來,就可以得到下面這一張圖:
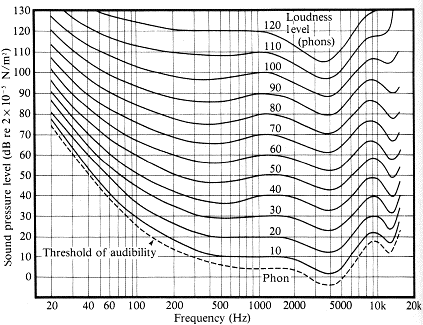
Curves of equal loudness determined experimentally by Fletcher, H. and Munson, W.A. (1933) J.Acoust.Soc.Am. 6:59.
The above figure also shows the sensitivity of the human ear with respect to frequency, which is simply the frequency response of the human ear. If you want to obtain the frequency response of your ears, you can jump to the the "Equal Loudness Tester" pages:
上面這一張圖,也代表人耳對於不同頻率的聲音的靈敏程度,這也就是人耳的頻率響應(Frequency Response)。如果你要測試你自己的耳朵的頻率響應,可以到這個網頁「Equal Loudness Tester」試試看:
Besides frequencies, the perceived loudness is also influenced by the the frame's timbre. For instance, we can try to pronounce several vowels using the same loudness level, and then plot the volume curves to see how they are related to the timbre or shapes/positions of lips/tongue, as shown in the following example.
主觀音量除了和頻率有關外,也和音訊的內容(音色或是基本週期的波形)有關,例如,我們可以盡量使用相同的主觀音量來錄下幾個發音比較單純的母音(ㄚ、ㄧ、ㄨ、ㄝ、ㄛ、ㄜ、ㄩ),然後再用音量公式來算它們的音量,就應該可以看出來音量公式和發音嘴型的關係。
From the above example, you can observed that though the perceived loudness is the same (click here to hear the recording), the computed volumes depend a lot on the timbers. In fact, we can perform another experiment to pronounce the same vowel but with different pitch to see how the perceived loudness depends on the fundamental frequency. This is left as an exercise.
Since the perceived loudness is easily affected by the fundamental frequency as well as the timber, we need to adjust the amplitudes accordingly when we are performing text-to-speech synthesis or singing voice synthesis.
主觀音量容易受到頻率和音色的影響,因此我們在進行語音或歌聲合成時,常常根據聲音的頻率和內容來對音訊的振福進行校正,以免造成主觀音量忽大忽小的情況。
Audio Signal Processing and Recognition (音訊處理與辨識)
