Tutorial on music genre classification
This tutorial explains the basics of music genre classification (MGC) using MFCC (mel-frequency cepstral coefficients) as the features for classification. The dataset used here is GTZAN dataseet.
Contents
Preprocessing
Before we start, let's add necessary toolboxes to the search path of MATLAB:
addpath d:/users/jang/matlab/toolbox/utility addpath d:/users/jang/matlab/toolbox/sap addpath d:/users/jang/matlab/toolbox/machineLearning addpath d:/users/jang/matlab/toolbox/machineLearning/externalTool/libsvm-3.21/matlab % For using SVM classifier
All the above toolboxes can be downloaded from the author's toolbox page. Make sure you are using the latest toolboxes to work with this script.
For compatibility, here we list the platform and MATLAB version that we used to run this script:
fprintf('Platform: %s\n', computer); fprintf('MATLAB version: %s\n', version); fprintf('Script starts at %s\n', char(datetime)); scriptStartTime=tic; % Timing for the whole script
Platform: PCWIN64 MATLAB version: 8.5.0.197613 (R2015a) Script starts at 04-Feb-2017 20:33:17
Dataset collection
First of all, we shall collect all the audio files from the corpus directory. Note that
- The audio files have extensions of "au".
- These files have been organized for easy parsing, with a subfolder for each class.
auDir='d:/dataSet/musicGenreClassification/GTZAN'; opt=mmDataCollect('defaultOpt'); opt.extName='au'; auSet=mmDataCollect(auDir, opt, 1);
Collecting 1000 files with extension "au" from "d:/dataSet/musicGenreClassification/GTZAN"...
Feature extraction
For each audio, we need to extract the corresponding feature vector for classification. We shall use the function mgcFeaExtract.m (which MFCC and its statistics) for feature extraction. We also need to put all the dataset into a single variable "ds" which is easier for further processing, including classifier construction and evaluation.
if ~exist('ds.mat', 'file') myTic=tic; opt=dsCreateFromMm('defaultOpt'); opt.auFeaFcn=@mgcFeaExtract; % Function for feature extraction opt.auFeaOpt=feval(opt.auFeaFcn, 'defaultOpt'); % Feature options opt.auEpdFcn=''; % No need to do endpoint detection ds=dsCreateFromMm(auSet, opt, 1); fprintf('Time for feature extraction over %d files = %g sec\n', length(auSet), toc(myTic)); fprintf('Saving ds.mat...\n'); save ds ds else fprintf('Loading ds.mat...\n'); load ds.mat end
Loading ds.mat...
Note that if feature extraction is lengthy, we can simply load ds.mat which has been save in the above code snippet.
Basically the extracted features are based on MFCC's statistics, including mean, std, min, and max along each dimension. Since MFCC has 39 dimensions, the extracted file-based features has 156 (= 39*4) dimensions. You can type try "mgcFeaExtract" on one of the audio file to plot the result:
auFile=[auDir, '/disco/disco.00001.au'];
figure; mgcFeaExtract(auFile, [], 1);
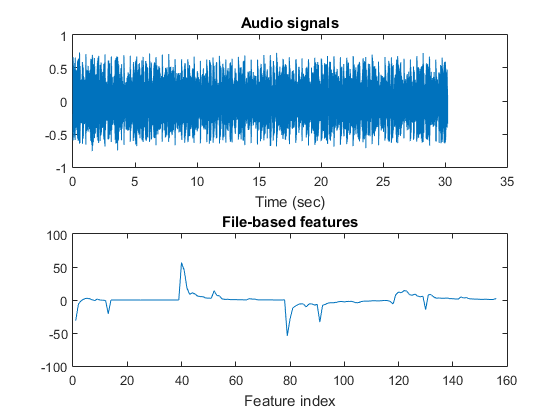
Dataset visualization
Once we have every piece of necessary information stored in "ds", we can invoke many different functions in Machine Learning Toolbox for data visualization and classification.
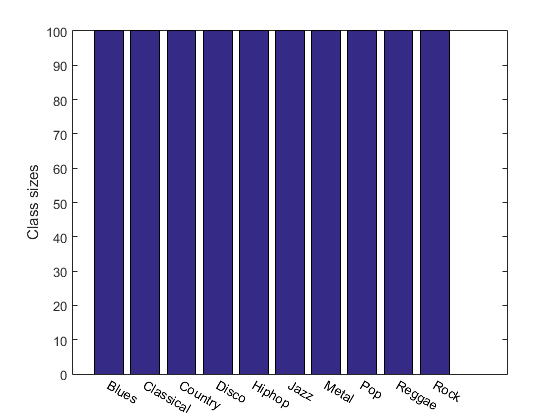
For instance, we can display the size of each class:
figure; [classSize, classLabel]=dsClassSize(ds, 1);
156 features 1000 instances 10 classes
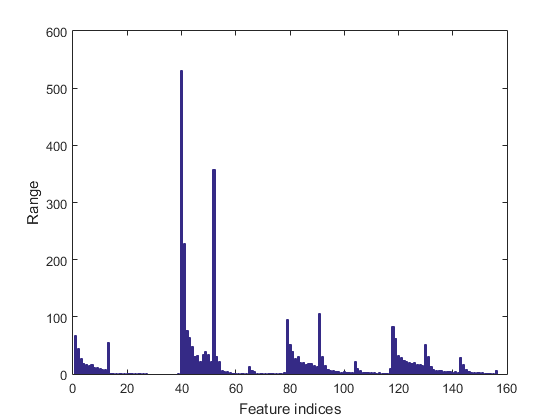
We can plot the range of features of the dataset:
figure; dsRangePlot(ds);
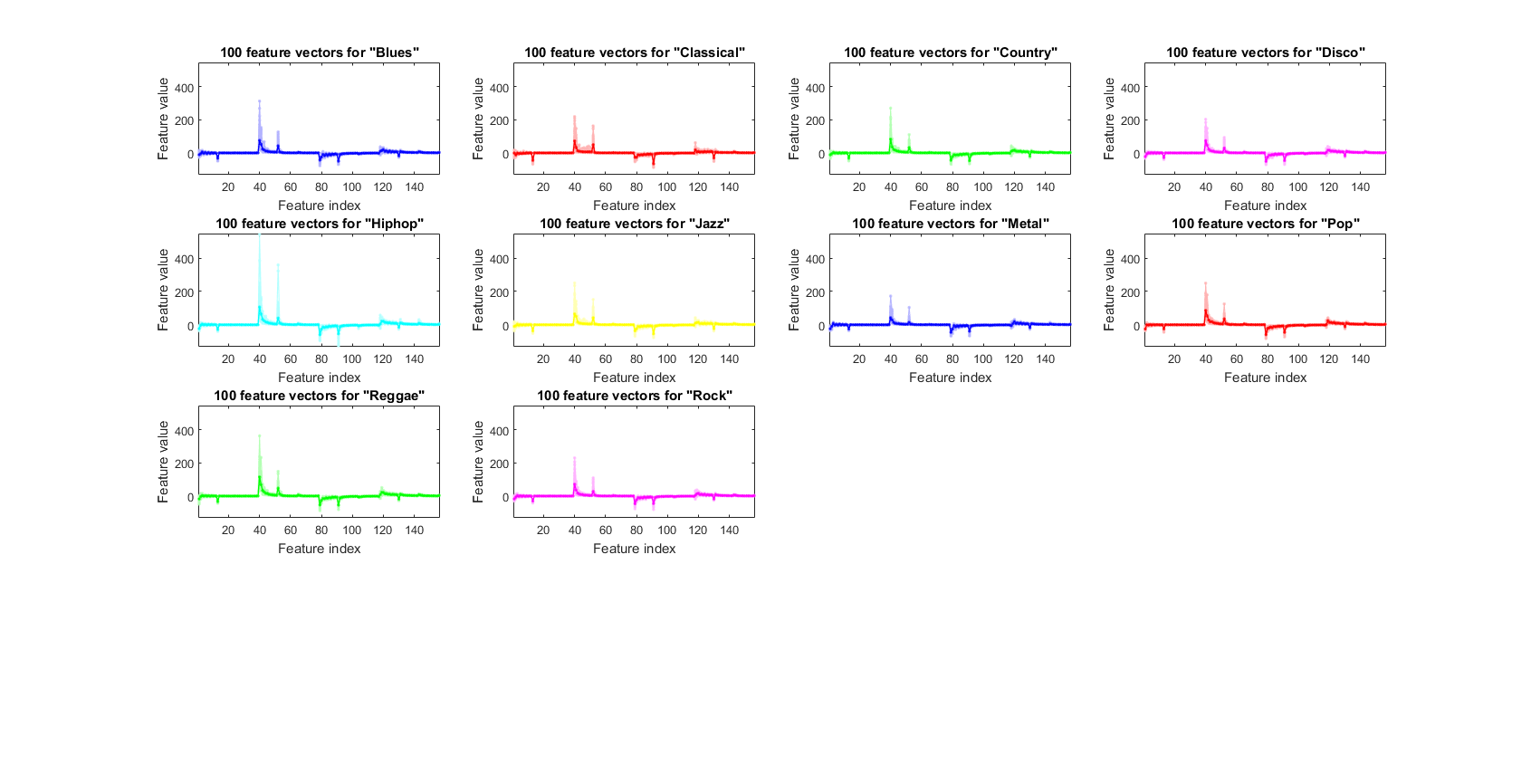
We can plot the feature vectors within each class:
figure; dsFeaVecPlot(ds); figEnlarge;
Dimensionality reduction
The dimension of the feature vector is quite large:
dim=size(ds.input, 1);
fprintf('Feature dimensions = %d\n', dim);
Feature dimensions = 156
We shall consider dimensionality reduction via PCA (principal component analysis). First, let's plot the cumulative variance given the descending eigenvalues of PCA:
[input2, eigVec, eigValue]=pca(ds.input); cumVar=cumsum(eigValue); cumVarPercent=cumVar/cumVar(end)*100; figure; plot(cumVarPercent, '.-'); xlabel('No. of eigenvalues'); ylabel('Cumulated variance percentage (%)'); title('Variance percentage vs. no. of eigenvalues');
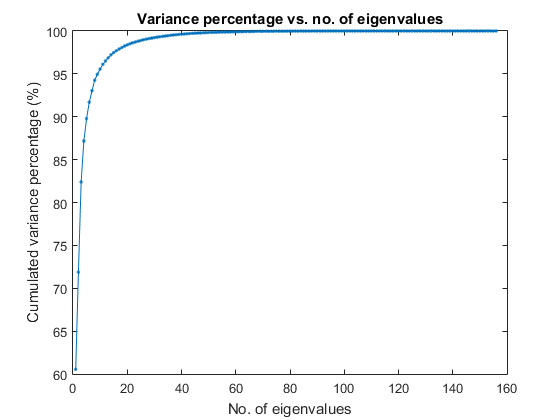
A reasonable choice is to retain the dimensionality such that the cumulative variance percentage is larger than a threshold, say, 95%, as follows:
cumVarTh=95;
index=find(cumVarPercent>cumVarTh);
newDim=index(1);
ds2=ds;
ds2.input=input2(1:newDim, :);
fprintf('Reduce the dimensionality to %d to keep %g%% cumulative variance via PCA.\n', newDim, cumVarTh);
Reduce the dimensionality to 10 to keep 95% cumulative variance via PCA.
However, our experiment indicates that if we use PCA for dimensionality reduction, the accuracy will be lower. As a result, we shall keep all the features for further exploration.
In order to visualize the distribution of the dataset, we can project the original dataset into 2-D space. This can be achieved by LDA (linear discriminant analysis):
ds2d=lda(ds); ds2d.input=ds2d.input(1:2, :); figure; dsScatterPlot(ds2d); xlabel('Input 1'); ylabel('Input 2'); title('Features projected on the first 2 lda vectors');
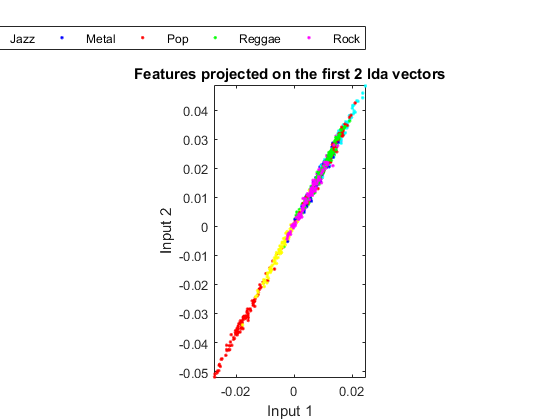
Apparently the separation among classes is not obvious. This indicates that either the features or LDA are not very effective.
Classification
We can try the most straightforward KNNC (k-nearest neighbor classifier):
[rr, ~]=knncLoo(ds); fprintf('rr=%g%% for original ds\n', rr*100); ds2=ds; ds2.input=inputNormalize(ds2.input); [rr2, computed]=knncLoo(ds2); fprintf('rr=%g%% for ds after input normalization\n', rr2*100);
rr=57.6% for original ds rr=64.9% for ds after input normalization
Again, the vanilla KNNC does not give satisfactory result. So we shall try other potentially better classifiers, such as SVM. Before try SVM, here we use a function mgcOptSet.m to put all the MGC-related options in a single file. This will be easier for us to change a single option in this file and check out the accuracy of MGC. Here is the code for using SVM:
myTic=tic; mgcOpt=mgcOptSet; if mgcOpt.useInputNormalize, ds.input=inputNormalize(ds.input); end % Input normalization cvPrm=crossValidate('defaultOpt'); cvPrm.foldNum=mgcOpt.foldNum; cvPrm.classifier=mgcOpt.classifier; plotOpt=1; figure; [tRrMean, vRrMean, tRr, vRr, computedClass]=crossValidate(ds, cvPrm, plotOpt); figEnlarge; fprintf('Time for cross-validation = %g sec\n', toc(myTic));
Fold = 100/1000 Fold = 200/1000 Fold = 300/1000 Fold = 400/1000 Fold = 500/1000 Fold = 600/1000 Fold = 700/1000 Fold = 800/1000 Fold = 900/1000 Fold = 1000/1000 Training RR=99.01%, Validating RR=77.00%, classifier=svmc, no. of folds=1000 Time for cross-validation = 490.748 sec
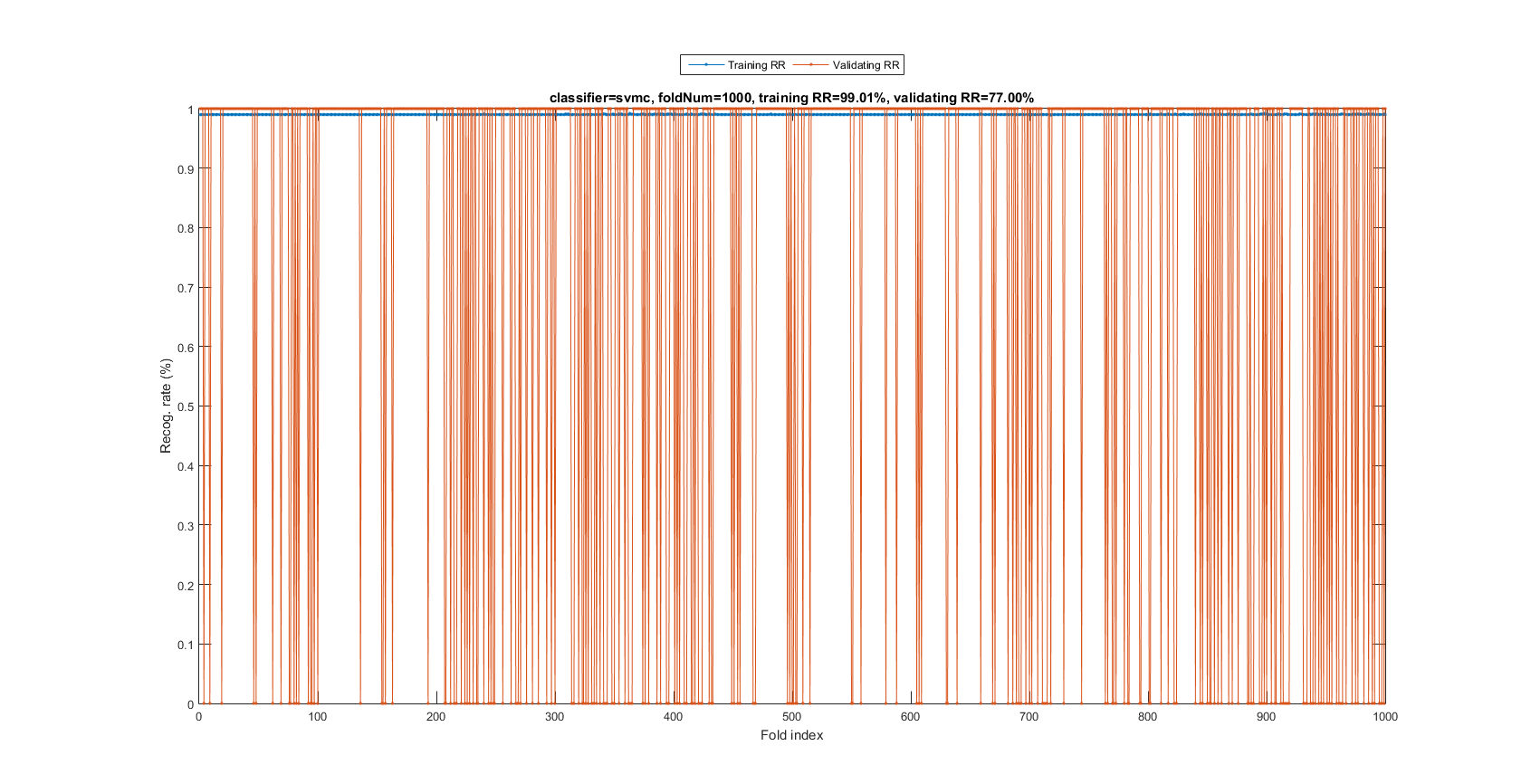
The recognition rate is 77%, indicating SVM is a much more effective classifier.
We can plot the confusion matrix:
for i=1:length(computedClass) computed(i)=computedClass{i}; end desired=ds.output; confMat = confMatGet(desired, computed); cmOpt=confMatPlot('defaultOpt'); cmOpt.className=ds.outputName; confMatPlot(confMat, cmOpt); figEnlarge;
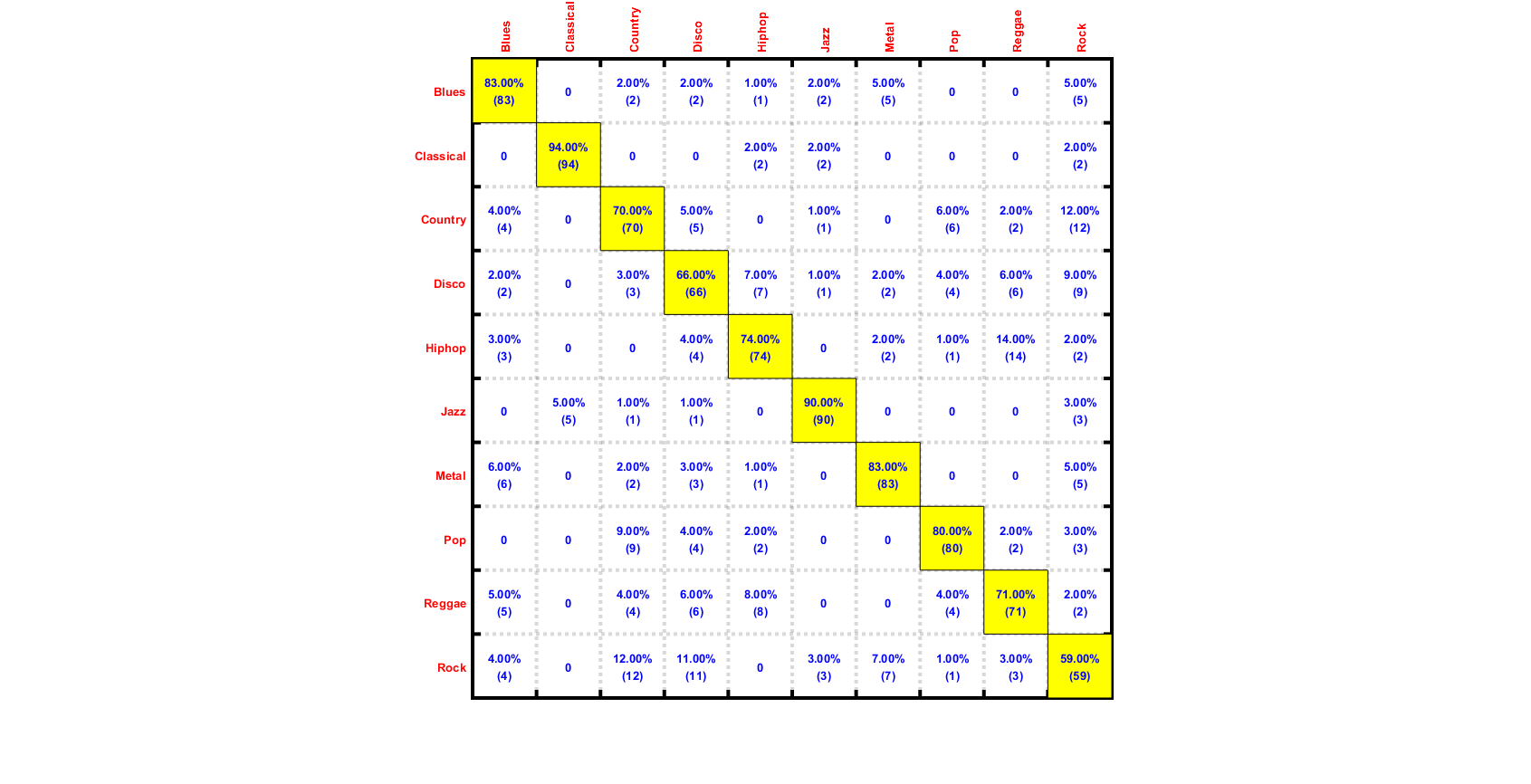
Summary
This is a brief tutorial on music genre classification based on MFCC's statistics. There are several directions for further improvement:
- Explore other features and feature selection for MGC
- Explore other classifiers (and their combinations) for MGC
Appendix
List of functions and datasets used in this script
Date and time when finishing this script:
fprintf('Date & time: %s\n', char(datetime));
Date & time: 04-Feb-2017 20:41:37
Overall elapsed time:
toc(scriptStartTime)
Elapsed time is 499.976553 seconds.